2022AP微积分BC北美卷FRQ已放出，附考情分析

各位AP小伙伴们好呀~2022年5月9日进行的AP微积分BC考试已经结束，本场考试为线下纸笔考试，CB官网已更新了2022AP微积分BC北美FRQ真题。

2022年AP微积分BC考试已经结束，本次北美卷的考题从难度系数来看是非常常规，整体简单，考试的方式非常友好。完全延续了疫情发生前2015-2019年真题的题目风格。在以往的真题中都可以找到类似的题目。

整体考试难度
本次考试对于完整刷过2015-2019年微积分题目的同学非常友好，今年的FRQ和往年的FRQ相比，基本上是一个模子里刻出来的。对整体微积分掌握到80%，就可以愉快的搞定这场考试，顺利拿到五分。

FRQ知识侧重
关于知识点的侧重，在数学考试中，依然还需要具备一些知识辨析的能力，单纯的记住知识点是没有用的，毕竟数学考试是考察思维的考试。即便是相似的知识，但依然需要具备完整的知识逻辑和思考逻辑，需要一定的列式和应对变化的能力，本次考试中可能会对同学们产生困扰的两个点：

1.变限积分考察中没有积分式，需要自己根据题干写出积分式，根据自己的积分式子进行后续问题的探讨。

2.不同定理的考察，FRQ中需要对IVT&MVT&积分求平均值的方法进行区分，特别是在原始信息已经是rate的基础上，这一点还是有一些难度。

知识点与解题思路
总结而言，本次考试中的FRQ需要一定的数学思维能力，但是要求并不高。

FRQ 1：
本题考察的是积分应用问题
(a)问是积分意义本身的考察，直接将速度进行积分就可以得到数量。
(b)问考察的是积分中值定理，将rate积分后除以时间跨度，可以得到平均数值。
(c)问则是导数应用单调性问题，利用导数的正负判断单调性。
(d)问是导数应用求最大值的问题，对给定函数求导，借助计算器画图观察导数图像变化，借助导数图像分辨单调性，由此获得最大值得可能取值点，进行互相的比较，获得最大值。

FRQ 2：
本题考察的是二维运动问题
(a)问考察的是参数方程求导，直接利用参数求导公式运算即可。
(b)问考察二维速率，依然借助公式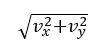获得结果。
(c)问考察位移问题，对y方向速度积分后加上初始值即可。
(d)问考察路程问题，直接利用公式。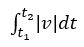

FRQ 3：
本题考察的是变限积分问题
(a)问以4作为起点，列出变限积分表达式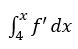，直接代值计算。
(b)问已知f’图像求拐点，根据f‘的单调性决定f’‘的正负变化，其中f’单调性发生改变的点即为拐点。
(c)、(d)问直接将函数求导，得到g‘=f’-1，将给定函数图像往下平移一个单位，进行(c)、(d)问的探究。

FRQ 4：
本题考察的是近似问题
(a)问考察近似求导的问题，直接两点联立近似求导。
(b)问考察介值定理，直接根据左右端点的数值进行推断。
(c)问考察黎曼近似，取右端点的高度进行面积计算近似。
(d)问考察相关变化率，这个题目是双变量的相关变化率，直接对表达式进行求导，其中h与r的变化率都可以从题干中找到。

FRQ 5：
本题考察的是积分的几何应用
(a)问考察积分求面积，直接在给定区域上进行定积分求面积。
(b)问考察定截面图形求体积，利用积分公式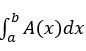，代入表达式进行积分运算，值得一提的是，这个题目进行积分的时候需要使用分部积分法。
(c)问考察反常积分的内容，将给定面积的上下限定为3&∞，进行正常积分计算即可。

FRQ 6：
本题考察的是泰勒级数
(a)问考察的比值法，直接借助比值法公式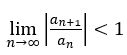，计算x的区间范围。
(b)问考察交替级数误差，这个题目表达的相对隐晦，其中误差是表达式第二项。
(c)、(d)问直接对交替级数本身求导运算即可，根据表达式进行·求值。

整体而言，2022年北美卷试题考察的方式非常中规中矩，知识点也是以往考试的热门知识点，如果单纯进行题目难度系数的横向对比，和以往年份的题目难度系数相差无几。但是鉴于已经有了前面年份的题目作为参考，在2022年面对这种相似的题目，可以说是考察的更加简单了。