排序算法精讲-优快云博客

本文链接：https://blog.youkuaiyun.com/linshuo1994/article/details/83268688

本文深入讲解了各种排序算法，包括冒泡排序、插入排序、归并排序、快速排序等，详细分析了每种算法的最优、平均和最差时间复杂度，以及空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

		最优	平均	最差	空间
稳定排序	冒泡排序	O(n) (数据正序，只需要走一趟即可完成排序。所需的比较次数C和记录移动次数M均达到最小值，即 $C_{min}=n-1;M_{min}=0$ )	O(n2)	O(n2) (数据是反序的，则需要进行n-1趟排序。每趟排序要进行n-i次比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值 $\begin{matrix} C_{max} = \frac{n(n-1)}{2} = O(n^{2})\\ M_{max} = \frac{3n(n-1)}{2} = O(n^{2}) \end{matrix}$ )	O(1)
	插入排序	O(n+m) (m为逆序的元素个数，最优m=0, $C_{min}=n-1;M_{min}=0$ )	O(n2)	O(n2) $C_{min}=n^{2}/2;M_{min}=n^{2}/2$	O(1)
	归并排序	O(n)	O(nlogn)	O(nlogn)	o(n)
	桶排序	O(n)	O(n+N)	O(n+N) (元素个数为n，元素处于[0,N]区间)	O(n+N)
	基数排序	O(d(n+N))	O(d(n+N))	O(d(n+N)) (令n为数据个数，d为数据位数.N为取值范围最大值)	O(N)
不稳定排序	选择排序	O(n) $C_{min}=n^{2}/2;M_{min}=0$	O(n2)	O(n2) $C_{min}=n^{2}/2;M_{min}=n-1$
	快速排序	O(n)	O(nlogn)	O(n2)	O(logn)
	希尔排序	O(n)	O(n1.3)	O(n2)	O(1)
	堆排序	O(n)	O(nlogn)	O(nlogn)	O(1)

冒泡排序(Bubble Sort)

依次比较两个相邻的元素，将小数放在前面，大数放在后面. N个数字要排序完成，总共进行N-1趟排序，每i趟的排序次数为(N-i)次

def BubbleSort(S):
    for i in range(len(S) - 1):
        for j in range(len(S) - i - 1):
            if S[j] > S[j+1]:
                S[j] , S[j+1] = S[j+1], S[j]

    return S

选择排序(Selection Sort)

不断地选择剩余元素之中的最小者，并交换到左边相应的顺序位置

运行时间和输入序列是否有序无关。一个有序数组和一个随机排序数组的排序时间竟然一样,对于长度为N的数组，比较次数与数组的初始状态无关，总的比较次数为： $(N-1)+(N-2)+...+2+1 = N(N-1)/2 = N^{2}/2$
数据移动最少。使用了N次交换，交换次数和数组大小是线性关系

def SelectionSort(S):
    for i in range(len(S) - 1):
        min = i
        for j in range(i+1, len(S)):
            if S[min] > S[j]:
                min = j
        S[i], S[min] = S[min], S[i]

插入排序(Insertion Sort)

将一个待排序元素，插入到已经有序的序列中的适当位置。

插入排序所需的时间取决于输入中元素的初始顺序

def InsertionSort(S):
    for i in range(1 ,len(S)):
        current = S[i]
        while i > 0 and S[i-1] > current:
            S[i], S[i-1] = S[i-1], S[i]
            i -= 1

def InsertionSort1(S):
    for i in range(1 ,len(S)):
        for j in range(i):
            if S[j-1] > S[j]:
                S[i], S[i - 1] = S[i - 1], S[i]

希尔排序(Shell's Sort)

缩小增量排序：希尔排序是插入排序改良的算法，希尔排序步长从大到小调整，第一次循环后面元素逐个和前面元素按间隔步长进行比较并交换，直至步长为1，步长选择是关键。

def ShellSort(S):
    L = len(S)
    h = 1
    while h <= L/3:        #1,4,13,40....
        h = h*3 + 1
    while h >= 1:
    """插入排序"""
        for i in range(h, L):
            current = S[i]
            while i >= h and S[i - h] > current:
                S[i], S[i - h] = S[i - h], S[i]
                i -= h
        
        h = h//3

归并排序(Merge Sort)

设有两个有序（升序）序列存储在同一数组中相邻的位置上，不妨设为A[l..m]，A[m+1..h]，将它们归并为一个有序数列，并存储在A[l..h]。其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlog2n)。

递归实现

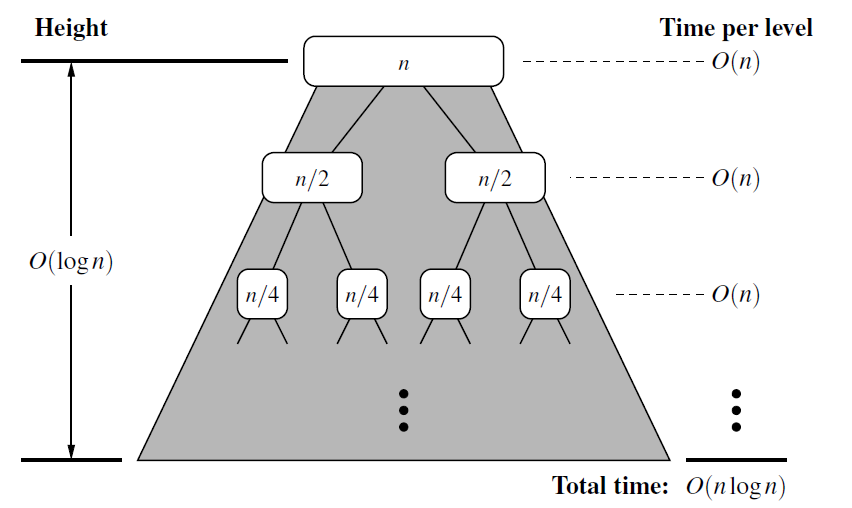
归并排序复杂度分析：一趟归并需要将待排序列中的所有记录扫描一遍，因此耗费时间为O(n),而由完全二叉树的深度可知，整个归并排序需要进行[log2n],因此，总的时间复杂度为O(nlogn),而且这是归并排序算法中平均的时间性能。空间复杂度：由于归并过程中需要与原始记录序列同样数量级的存储空间去存放归并结果及递归深度为log2N的栈空间，因此空间复杂度为O(n+logN)，就是说，归并排序是一种比较占内存，但却效率高且稳定的算法

def MergeSort(list):
    """利用回归实现"""
    if len(list) <=1:
        return list
    num = len(list)//2
    left = MergeSort(list[:num])
    right = MergeSort(list[num:])
    return Merge(left, right)

def Merge(left, right):
    r, l = 0, 0
    result = []
    while l<len(left) and r < len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    #如果有剩下的，那么说明就是它是比前面的数组都大的，直接加入就可以了
    result += left[l:]
    result += right[r:]
    return result

利用数组实现

def merge_sort(S):
    """利用数组实现"""
    n = len(S)
    if n < 2:
        return S
    mid = n // 2
    S1 = S[:mid]
    S2 = S[mid:]
    merge_sort(S1)
    merge_sort(S2)
    merge(S1, S2, S)

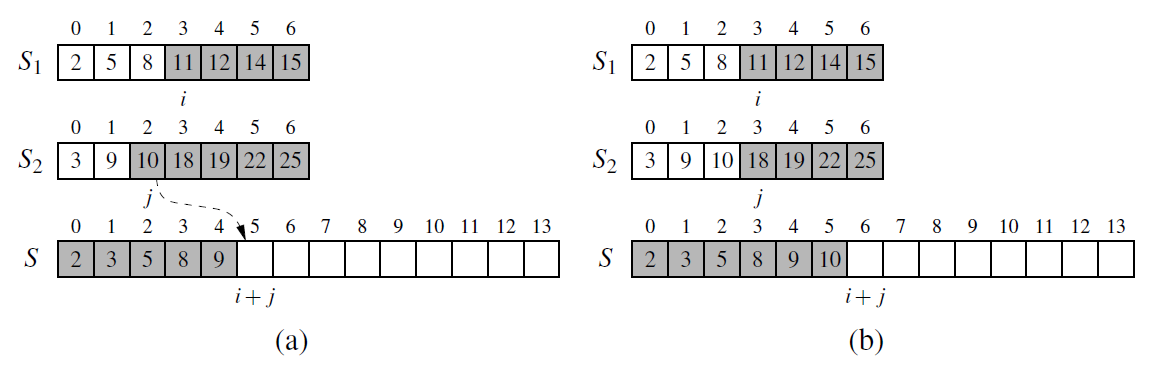
def merge(S1, S2, S):
    i = j = 0
    while i + j < len(S):
        # 将S1和S2元素重新写入并覆盖掉S，可以将S看作新的空列表
        if j == len(S2) or (i < len(S1) and S1[i] < S2[j]):
          S[i+j] = S1[i]
          i += 1
        else:
            S[i+j] = S2[j]
            j += 1

迭代实现（非递归）

非递归的方法，避免了递归时深度为log2N的栈空间，空间只是用到归并临时申请的跟原来数组一样大小的空间，并且在时间性能上也有一定的提升，因此，使用归并排序是，尽量考虑用非递归的方法。

import math

def merge(src, result, start, inc):
  """合并src[start:start+inc] 与 src[start+inc:start+2*inc]"""
  end1 = start+inc
  end2 = min(start+2*inc, len(src))
  x, y, z = start, start+inc, start

  #下面循环结束的条件有两个，如果是左边的游标尚未到达，那么需要把数组接回去，可能会有疑问，那如果右边的没到达呢，其实模拟一下就可以
  # 知道，如果右边没到达，那么说明右边的数据比较大，这时也就不用移动位置了

  while x < end1 and y < end2:            #如果左边的数据还没达到分割线且右边的数组没到达分割线，开始循环
    if src[x] < src[y]:
      result[z] = src[x]
      x += 1
    else:
      result[z] = src[y]
      y += 1
    z += 1
  if x < end1:
    result[z:end2] = src[x:end1]
  elif y < end2:
    result[z:end2] = src[y:end2]

def merge_sort(S):

  n = len(S)
  logn = math.ceil(math.log(n,2))
  src, dest = S, [None] * n
  for i in (2**k for k in range(logn)):     #逐级上升，第一次比较2个，第二次比较4个，第三次比较8个。。。
    for j in range(0, n, 2*i):
      merge(src, dest, j, i)
    src, dest = dest, src
  if S is not src:
    S[0:n] = src[0:n]

快速排序(Quick sort)

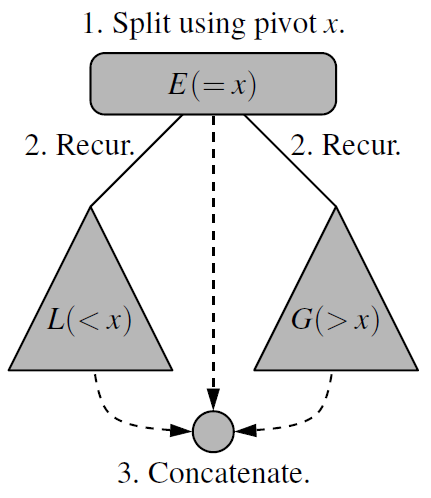
在数组中随机选一个数（默认数组首个元素），数组中小于等于此数的放在左边，大于此数的放在右边，再对数组两边递归调用快速排序，重复这个过程。

1.利用多个队列实现

def quick_sort(S):
  """Sort the elements of queue S using the quick-sort algorithm."""
  n = len(S)
  if n < 2:
    return                            # list is already sorted
  # divide
  p = S.first()                       # using first as arbitrary pivot
  L = LinkedQueue()
  E = LinkedQueue()
  G = LinkedQueue()
  while not S.is_empty():             # divide S into L, E, and G
    if S.first() < p:
      L.enqueue(S.dequeue())
    elif p < S.first():
      G.enqueue(S.dequeue())
    else:                             # S.first() must equal pivot
      E.enqueue(S.dequeue())
  # conquer (with recursion)
  quick_sort(L)                       # sort elements less than p
  quick_sort(G)                       # sort elements greater than p
  # concatenate results L -> E -> G
  while not L.is_empty():
    S.enqueue(L.dequeue())
  while not E.is_empty():
    S.enqueue(E.dequeue())
  while not G.is_empty():
    S.enqueue(G.dequeue())

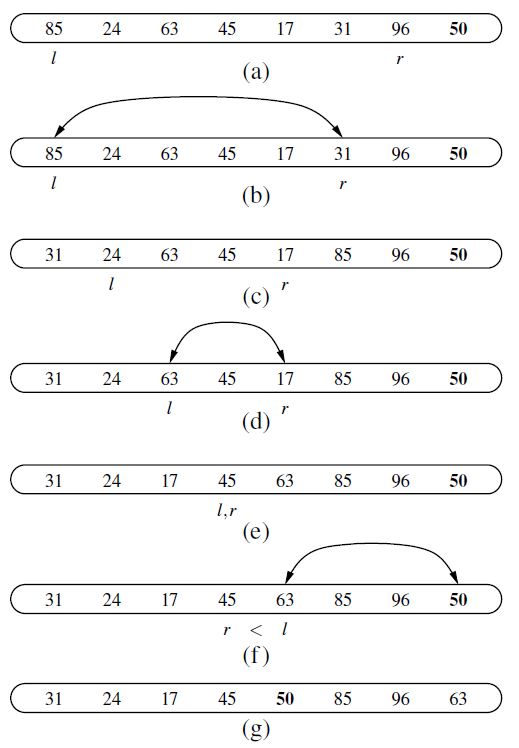
2.利用原地替换实现(in-place quick-sort)

def quickSort(S, a, b):
  if a >= b:
    return S                                   
  pivot = S[b]                                          
  left = a                                               
  right = b-1                                            
  while left <= right:
    while left <= right and S[left] < pivot:
      left += 1
    while left <= right and pivot < S[right]:
      right -= 1
    if left <= right:                                   
      S[left], S[right] = S[right], S[left]             
      left, right = left + 1, right - 1                 

  # put pivot into its final place (此时left > right)
  S[left], S[b] = S[b], S[left]
  quickSort(S, a, left - 1)
  quickSort(S, left + 1, b)

  return S

堆排序(Heap Sort)

首先将数组元素建成大小为n的大顶堆，堆顶（数组第一个元素）是所有元素中的最大值，
将堆顶元素和数组最后一个元素进行交换，再将除了最后一个数的n-1个元素建立成大顶堆，再将最大元素和数组倒数第二个元素进行交换
重复直至堆大小减为1。

大顶堆是具有以下性质的完全二叉树：每个节点的值都大于或等于其左右孩子节点的值。即根节点是堆中最大的值，按照层序遍历给节点从1开始编号，则节点之间满足如下关系：

利用利用python内置堆结构实现

import heapq

def HeapqSort(S):
    h = []
    for value in S:
        heapq.heappush(h, value)
    return [heapq.heappop(h) for i in range(len(h))]

def heap_sort(lst):
    for start in range(len(lst) - 1, -1, -1):
        siftdown(lst, start, len(lst) - 1)
    for end in range(len(lst) - 1, 0, -1):
        lst[end], lst[0] = lst[0], lst[end]
        siftdown(lst, 0, end - 1)
    return lst

def siftdown(lst, start, end):
    root = start
    while True:
        child = 2 * root + 1
        if child > end: break
        if child + 1 <= end and lst[child] < lst[child + 1]:
            child += 1
        if lst[child] > lst[root]:
            lst[child], lst[root] = lst[root], lst[child]
            root = child
        else:
            break

利用优先队列实现

from DataStructure.Queue.HeapPriorityQueue import HeapPriorityQueue


def HPQSort(S):
    HQ = HeapPriorityQueue(S.copy())    #HeapPriorityQueue自定义优先队列
    for i in range(len(S) - 1, -1, -1):
        HQ._upheap(i)
    for end in range(len(S)-1, -1, -1):
        S[len(S)-end-1] = HQ._data[0]
        HQ._swap(0, len(HQ._data) - 1)  # put minimum item at the end
        HQ._data.pop()  # and remove it from the list;
        HQ._downheap(0)  # then fix new root    return S
    return S

桶排序(Bucket Sort)

根据数据规模n划分m个相同大小的区间（每个区间为一个桶，桶可理解为容器）
将n个元素按照规定范围分布到各个桶中去,对每个桶中的元素进行排序，排序方法可根据需要，选择快速排序，或者归并排序，或者插入排序
依次从每个桶中取出元素，按顺序放入到最初的输出序列中(相当于把所有的桶中的元素合并到一起)

桶可以通过数据结构链表实现。桶排序的时间代价，假设有m个桶，则每个桶的元素为n/m，

当辅助函数为冒泡排序O(n2) ,桶排序为 O(n)+mO((n/m)2)
当辅助函数为快速排序时O(nlgn), 桶排序为 O(n)+mO(n/m log(n/m))

通常桶越多，执行效率越快，即省时间，但是桶越多，空间消耗就越大，是一种通过空间换时间的方式。

Algorithm bucketSort(S):
    Input: Sequence S of entries with integer keys in the range [0,N−1]
    Output: Sequence S sorted in nondecreasing order of the keys
    let B be an array of N sequences, each of which is initially empty

    #入桶
    for each entry e in S do
        k = the key of e
        remove e from S and insert it at the end of bucket (sequence) B[k]

    #合并    
    for i = 0 to N−1 do
        for each entry e in sequence B[i] do
            remove e from B[i] and insert it at the end of S

基数排序(Radix Sort)

基数排序是基于数据位数的一种排序算法。将整数按位数切割成不同的数字，然后按每个位数分别比较
它有两种算法

LSD–Least Significant Digit first 从低位（个位）向高位排。
MSD– Most Significant Digit first 从高位向低位（个位）排。

LSD的基数排序适用于位数小的数列，如果位数多的话，使用MSD的效率会比较好

import math
 
def sort(a, radix=10):
    """a为整数列表， radix为基数"""
    K = int(math.ceil(math.log(max(a), radix))) # 用K位数可表示任意整数
    bucket = [[] for i in range(radix)] # 不能用 [[]]*radix
    for i in range(1, K+1): # K次循环
        for val in a:
            bucket[val%(radix**i)/(radix**(i-1))].append(val) # 析取整数第K位数字 （从低到高）
        del a[:]
        for each in bucket:
            a.extend(each) # 桶合并
        bucket = [[] for i in range(radix)]