KMP 算法

最新推荐文章于 2024-08-28 20:45:23 发布

Mona______

最新推荐文章于 2024-08-28 20:45:23 发布

阅读量1k

点赞数

分类专栏： # 类型总结之——常见算法篇数据结构与算法总结篇文章标签：算法数据结构

本文链接：https://blog.youkuaiyun.com/linping_/article/details/117173899

版权

数据结构与算法总结篇同时被 2 个专栏收录

12 篇文章

订阅专栏

类型总结之——常见算法篇

1 篇文章

订阅专栏

1、KMP算法

KMP 就是三位创造者的名字缩写 Knuth，Morris和Pratt

KMP 是为了解决字符串匹配的问题，极大的提高的搜索的效率。通俗来讲也就是在一个串中查找是否出现过另一个串

KMP 算法的时间复杂度是O(n+m)，对比暴力解法时间复杂度是 O（m*n），其中m n 是文本串与模式串的长度

KMP 经典思想就是: 当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。

讲解过程中使用的例子：

文本串： aabaabaaf
模式串： aabaaf
求文本串与模式串完全匹配的子串

KMP算法要使用前缀表来解决问题。

1、那么什么是前缀表？

1、什么是前缀？以模式串举例。
概念：包含首字母，不包含尾字母的所有子串。

a
aa
aab
aaba
aabaa

2、什么是后缀
概念：包含尾字母，不包含首字母的所有子串。

f
af
aaf
baaf
abaaf

3、前缀表的含义是什么呢？
前缀表里的数值代表着就是：当前位置之前的子串有多大长度相同的前缀后缀。

4、前缀表有什么作用呢？
前缀表是用来回溯的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

2、什么是最长相等前后缀?

也有人称之为求最长公共前后缀
以模式串举例，n=6，注意这个就需要一个一个来分析了。
逐个来分析前k（范围1-n）个字符组成的子串的前缀表和后缀表，求其中前缀表和后缀表中最长相等子串，
由此即可得到前缀表为：

aabaaf
010120

对于 a 的最长相等前后缀长度为：0
既没有前缀，也没有后缀，首字母即尾字母，所以为 0

对于 aa 的最长相等前后缀长度为：1
前缀为a，后缀为a，因此为1，

对于 aab 的最长相等前后缀长度为：0
因为最后是b,所以找不到与其相等的前后缀，为 0

对于 aaba 的最长相等前后缀长度为：1
因为只有第一个a与最后一个a做后缀，故为1,

对于 aabaa 的最长相等前后缀长度为：2
前缀表中的前两个aa，与后缀表中的后两个aa相等，故长度为2

对于 aabaaf 的最长相等前后缀长度为：0
显然为0。

3、如何匹配？

由上一步得到前缀表（prefix table），如何来进行匹配呢？
理解点睛：

当找到不匹配的位置时（在f处），要找它前面的子串（aabaa）的最长相等前后缀(最大是2)。
我们了解到对于它前面的这个子串（aabaa），有一个前缀aa，等于后缀aa，
现在是在这个后缀aa的后面不匹配了，
那我们就要找到与其（后缀aa) 相等的前缀（前缀aa）的后面开始匹配，
所以就是找到了b对应的位置，
也刚好就是最长相等前后缀（长度为2）对应的下标（下标从0开始，刚好是第三个字母）

4、next数组3种写法

next数组的三种写法，前缀表通常放在 next 数组中，

next数组1、直接存为前缀表
a a b a a f
0 1 0 1 2 0

next数组2、整体减1 主要记这个方法
a a b a a f
-1 0 -1 0 1 -1

next数组3、整体右移，且把第一个变为-1
a a b a a f
-1 0 1 0 1 2

在后续处理的过程中，不同人会有不同的解法，但是处理思路是相通的

5、next数组2 具体实现

void getNext(int* next, const string& s) 
{
    int j = -1;
	// next[i]表示 i(包括i) 之前最长相等的前后缀长度，
	// 其实就是j,所以有 next[i]=j
    next[0] = j;
    for(int i = 1; i < s.size(); i++) 
	{ // 注意i从1开始
        while (j >= 0 && s[i] != s[j + 1]) 
		{ // 前后缀不相同了
            j = next[j]; // 向前回溯
        }
        if (s[i] == s[j + 1]) 
		{ // 找到相同的前后缀
            j++;
        }
		// next[i]表示 i(包括i) 之前最长相等的前后缀长度，
		// 其实就是j,所以有 next[i]=j
        next[i] = j; 
    }
}

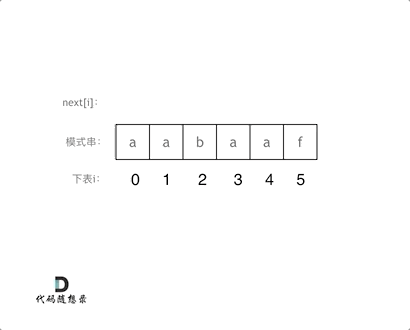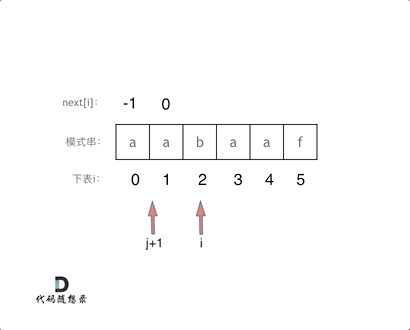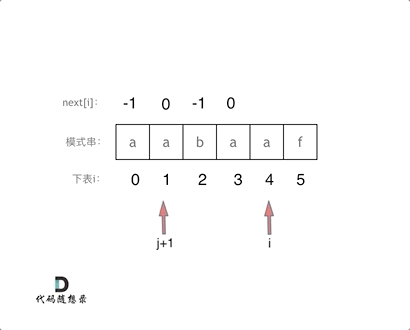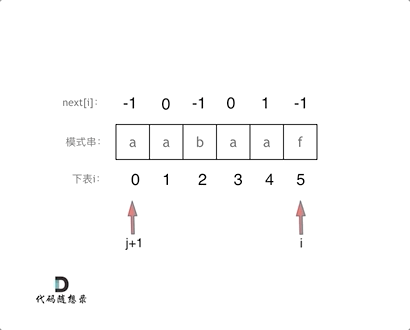
avatar

涉及到双指针的思想

定义两个指针，j 指向前缀终止位置-1的位置。 i 指向后缀位置-1的位置
相当一个在控制前缀位置，一个在控制后缀位置。

1、初始化：
next[i]表示 i(包括i) 之前最长相等的前后缀长度，其实就是j,所以有 next[i]=j

2、处理前后缀不相同的情况
因为j初始化为 -1，那么i就从1开始，比较的两者是 s[i]和s[j+1]
如果两者不同，也就是前后缀末尾不同，就向前回溯，
回溯时就要看前缀表了，也就是next数组
也就是就要找 j+1 前一个元素在next数组里的值（就是next[j]）

next[j]就是记录着j(包括j)之前的子串的相同前后缀的长度

3、处理前后缀相同的情况
此时要做两步：

一是将 i 和 j 同时向后移（也就是+1）
二是将j(也就是前长度)赋值给next[i]
别忘了 next[i]要记录相同前后缀的长度

6、next数组1 具体实现

void getNext(int* next, const string& s) 
{
    int j = 0;
    next[0] = 0;
    for(int i = 1; i < s.size(); i++) 
	{
        while (j > 0 && s[i] != s[j]) 
		{ // j要保证大于0，因为下面有取j-1作为数组下表的操作
            j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
        }
        if (s[i] == s[j]) {
            j++;
        }
        next[i] = j;
    }
}

7、代码实现讲解

s 表示模式串，t表示文本串

一、构造next数组，其实就是计算模式串的前缀表的过程，主要有三个步骤

1、初始化（不同的实现，初始化也不同）

2、处理前后缀不相同的情况

3、处理前后缀相同的情况

这里涉及到双指针的思想

二、找到next数组后，用它来做匹配，

依然是需要定义两个指针，也就是两个下标
j 指向模式串的起始位置，
i 指向文本串的起始位置。
比较对象是t[i]与s[j+1]

1、初始化（j从-1开始[因为next数组里记录的起始位置为-1]，i从0 开始）
2、处理 t[i]与s[j+1] 不同的情况
j 从next数组里找寻下一个匹配的位置

3、处理 t[i]与s[j+1] 相同的情况
i 和 j 同时向后移，

三、关于返回值 —— 文本串中找出模式串出现的第一个位置
i - 模式串长度 + 1

8、补充说明

1、若 next[len - 1] == -1 ，则表明该字符串中没有最长相等的前后缀
2、若 next[len - 1] != -1 ，则表明该字符串中有最长相等的前后缀
3、根据next数组可知，最长相等前后缀的长度为： next[len-1]+1，** 设为x **.
也就是next数组的最后一个元素 +1
4、若 len % (len-x) == 0 , 则表明有该字符串重复的子字符串。

辅助理解的一条评论：
如果答案是 true 的话，next 表前几位（子字符串）都是 -1，后边将是一直递增，next（n－1）＋1存放的就是原字符串减去子字符串长度的值，记为len2，将 len－len2的值记为len1，它就是子字符串的长度，一定是可以被 len 整除的！

9、一条辅助性提问：

1、想知道为什么前缀表取名叫next而不是见名知意叫prefix

可能是kmp里用的前缀表已经不是真正的前缀表了（做了减1的调整），所以叫做next很好一些吧，就是求下一个匹配的位置。也有的实现代码会写prefix，但是还是写next居多，知道原理就行了

10、代码实现

用 build 去找s的nxt数组，
果最长前后缀 = nxt[n] = nxt.back()
先找最长前后缀，如果最长前后缀不是0的话，那么用 n-nxt[n] 就是模式串的长度
如果整个串的长度是模式串的整数倍的话，说就是 true

build 得到的nxt数组就表示，p字符串中的最长前后缀个数
nxt 最后一位表示这个串的最长前后缀个数
nxt 最后一位表示这个串的最长前后缀个数
nxt 最后一位表示这个串的最长前后缀个数

    // 得到模式串的next数组，next数组的长度是 p 的长度 +1,，因为最后一位是 自己追加的永远不可能匹配的位置
    vector<int> Build(const string& p)
    {
        const int m = p.length();
        // 前两位先设为0，因为是 p 与 p 自己进行比较，所以需要有一位的错位，所以 i 从 1 开始，j 从 0 开始
        vector<int> nxt{0, 0};  
        // 从 1 开始遍历
        for (int i = 1, j = 0; i < m; ++i)
        {
            while (j > 0 && p[i] != p[j])   j = nxt[j];
            if (p[i] == p[j])   ++j;

            // 存储 next 数组
            nxt.push_back(j);
        }
        return nxt;
    }

    vector<int> Match(const string& s, const string& p)
    {
        vector<int> nxt(Build(p));
        vector<int> ans;
        const int n = s.length();
        const int m = p.length();
        for (int i = 0, j = 0; i < n; ++i)
        {
            // 情况一：不等
            while (j > 0 && s[i] != p[j])   j = nxt[j];
            // 情况二：相等
            if (s[i] == p[j])   ++j;

            // 这里是为了存储在s中第一个完全与p匹配的字符对应的下标，相当于下一次跳转到 j=nxt[j]，也是不匹配的跳转
            if (j == m)
            {
                // 保存 s中第一个完全与p匹配的字符的对应下标
                ans.push_back(i - m + 1);   // ???? 这个 ans 存的什么？？？？？？,
                j = nxt[j];
            }
        }
        return ans;
    }

2、字典序

什么叫字典序？

顾名思义就是按照字典的排列顺序。

对于字符串，先按首字符排序，如果首字符相同，再按第二个字符排序，以此类推。

如aa,ab,ba,bb,bc就是一个字典序。

以字典序为基础，我们可以得出任意两个数字串的大小。

比如 “1” < “12”<“13”。就是按每个数字位逐个比较的结果。
对于一个数字串的排列，可以知道最小的排列是从小到大的有序串“123456789”，

而最大的排列串是从大到小的有序串“987654321”。

这样对于“123456789”的所有排列，将他们排序，即可以得到按照字典序排序的所有排列的有序集合。

当我们知道当前的排列时，要获取下一个排列时，就可以找到有序集合中的下一个数（恰好比它大的）。

比如，当前的排列时“123456879”，那么恰好比它大的下一个排列就是“123456897”。

当目前的排列是最大的时候，说明所有的排列都找完了。

2、Manacher算法总结

俗称“马拉车”算法，也是一种处理字符串的算法。

应用范围相比于KMP要窄得多，求 最长回文子串

计算最长回文子串的方法总结

暴力解法

枚举该字符串中的每一个子串，然后判断是否为回文串
时间复杂度为O(n^3)

优化版暴力解法

优化的思想是枚举回文串的中点，首先需要根据回文串长度为奇数和偶数两种情况
根据奇偶的不同分情况判断是否是回文串
时间复杂度为O(n^2)

Manacher算法原理

时间复杂度为O(n)，线性的时间复杂度
将长度为奇数的回文串和长度为偶数的回文串一起考虑

Manacher算法步骤

在原字符串的每个相邻两个字符中间插入一个分隔符，同时在首尾也要添加一个分隔符，分隔符的要求是不在原串中出现，一般情况下可以用#号。
Manacher算法用一个辅助数组Len[i]表示以字符T[i]为中心的最长回文字串的最右字符到T[i]的长度，比如以T[i]为中心的最长回文字串是T[l,r],那么Len[i]=r-i+1。