算法竞赛进阶指南线性DP——I-country

什么是凸连通块
哪一面都没有凹进去的部分。凸出使得某一边上，会有一个点，这个点左右两侧的单调性单调性相反。
👉 左增右减
👉 左减右增

在处理过程中需要关注和哪些信息
1.要求包含k个，转移过程中要考虑已经包含了多少个，即已经选出的格子数。

2.可以从一个格子一个格子处理，也可以一行一行处理，但一个格子能够包含的信息太少，尤其是单调性方面，不好考虑。所以 从行的角度考虑，即一行一行进行转移

3.在处理过程中，将一个连通块分成若干行，考虑一行取哪些格子纳入选择范围，因为要连通，一行所选的数量一定是连续的，即可以设定一个左右边界，来表示这一行选出了哪些格子。

4.考虑在选择这一行的格子后，左右两侧轮廓的单调性是否会发生变化。

————————————

综上，以行为阶段，如果“阶段”不足以表示这个状态，则可以增加一些附加信息作为状态的维度。

这是一个多维的DP
f[i,j , l, r,x,y]表示前i 行选择了j个格子，其中第i 行选择了第l到r个格子（若不选则均为0)，左边界的单调性类型为x，右边界的单调性类型为y (0表示递增，1表示递减）时，能构成的凸连通块的最大权值和。

思考状态转移过程，即哪些情况可以转移到当前的 f 的状态中，

（1）左右两侧都扩张

前 i - 1行与i行之间的关系入下图
即需要满足 l ≤ p ≤ q ≤ r

在此情况下，分析各个维度值得转化情况

• 格子数 前i行选用j个格子，第i行选用格子数量为 r-l+1，则前i-1行选用格子 j-（r-l+1）
• 左边界 p，右边界 q
• 单调性，左侧单调递增，右侧单调递减
  so，
  
  f(i-1,0,0,0,1,0) 表示第一行没选格子。

（2）==左边扩张 右面缩减

前 i - 1行与i行之间的关系入下图
即需要满足 l ≤ p ≤ r ≤ q

在此情况下，分析各个维度值上一个阶段的情况

• 格子数 前i行选用j个格子，第i行选用格子数量为 r-l+1，则前i-1行选用格子 j-（r-l+1）
• 左边界 p，右边界 q
• 单调性，左侧单调递增，右侧单调讨论时，上一层的右侧的点有可能是是已经在上升（即缩减）的情况了，也有可能是刚开始缩减的点，即是拐点，即右轮廓的的单调性有可能上升也有可能下降，需要分情况讨论。
• 上一层已经处于收缩状态，f(i-1,j-(r-l+1),p,q,1,1)
• 上一层是刚开始收缩的点 ,f(i-1,j-(r-l+1),p,q,1,0)
  so，
  

（3）==左边缩减 右面扩张

满足条件 p ≤ l ≤ q ≤ r

右边一直都是扩张态，不影响
左边，发现了变化，有可能是上一行已经处于单调递减的情况了，也有可能是在这一行才开始递减的，上一行还是在增。

分情况处理

• 上一层已经处于收缩状态,即递减，f(i-1,j-(r-l+1),p,q,1,0)
• 上一层是刚开始收缩的点，递增 ,f(i-1,j-(r-l+1),p,q,0,0)
  

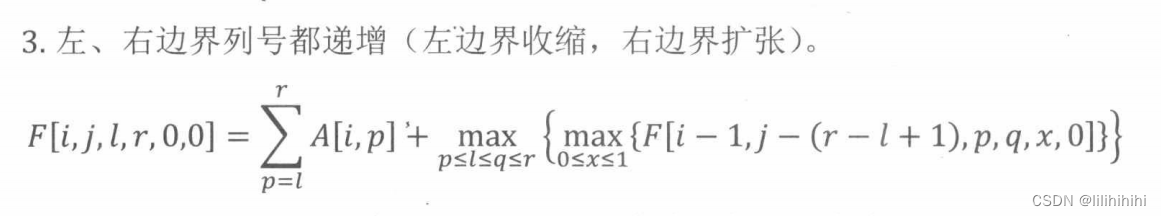
（4）==左边缩减 右面扩张

满足条件
p ≤ l ≤ r ≤ q

两边都收缩，都是递减状态，但左侧上一行可能是递增的最后一个，也可能已经是递减的了，右侧也一样。所以分4种情况讨论。

• 上一层左递减，右递减 f(i-1,j-(r-l+1),p,q,1,1)
• 上一层左递增，右递减 ,f(i-1,j-(r-l+1),p,q,0,1)
• 上一层左递减，右递增 ,f(i-1,j-(r-l+1),p,q,1,0)
• 上一层左递增，右递增 ,f(i-1,j-(r-l+1),p,q,0,0)
  -
  
  本题还要输出方案。在动态规划问题需要给出方案时，通常做法是额外使用一些与DP状态大小相同的数组记录下来每个状态的“最优解”是从何处转移而来的。最终，在DP求出最优解后，通过一次递归，沿着记录的每一步**“转移来源”回到初态**，即可得到一条从初态到最优解的转移路径，也就是所求的具体方案。

【代码实现】

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=16;
int n,m,k,a[N][N];
int f[N][N*N][N][N][2][2];

struct state{
    int i,j,l,r,x,y;
}g[N][N*N][N][N][2][2];
int main(){
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
        for(int j=0;j<=k;j++)
            for(int l=1;l<=m;l++)
                for(int r=l;r<=m;r++){
                    if(j<r-l+1)
                        continue ;
                    // left out, right out
                    {
                        int &tf=f[i][j][l][r][1][0];
                        state &tg=g[i][j][l][r][1][0];
                        for(int p=l;p<=r;p++)
                            for(int q=p;q<=r;q++){
                                int val=f[i-1][j-(r-l+1)][p][q][1][0];
                                if(tf<val){
                                    tf=val;
                                    tg=(state){i-1,j-(r-l+1),p,q,1,0};
                                }
                            }
                        for(int p=l;p<=r;p++)
                            tf+=a[i][p];
                    }
                    // left out, right decrease
                    {
                        int &tf=f[i][j][l][r][1][1];
                        state &tg=g[i][j][l][r][1][1];
                        for(int p=l;p<=r;p++)
                            for(int q=r;q<=m;q++)
                                for(int st=0;st<=1;st++){
                                    int val=f[i-1][j-(r-l+1)][p][q][1][st];
                                    if(tf<val){
                                        tf=val;
                                        tg=(state){i-1,j-(r-l+1),p,q,1,st};
                                    }
                                }
                        for(int p=l;p<=r;p++)
                            tf+=a[i][p];
                    }
                    // left decrease, right out.
                    {
                        int &tf=f[i][j][l][r][0][0];
                        state &tg=g[i][j][l][r][0][0];
                        for(int p=1;p<=l;p++)
                            for(int q=l;q<=r;q++)
                                for(int st=0;st<=1;st++){
                                    int val=f[i-1][j-(r-l+1)][p][q][st][0];
                                    if(tf<val){
                                        tf=val;
                                        tg=(state){i-1,j-(r-l+1),p,q,st,0};
                                    }
                                }
                        for(int p=l;p<=r;p++)
                            tf+=a[i][p];
                    }
                    // both decrease
                    {
                        int &tf=f[i][j][l][r][0][1];
                        state &tg=g[i][j][l][r][0][1];
                        for(int p=1;p<=l;p++)
                            for(int q=r;q<=m;q++)
                                for(int x=0;x<=1;x++)
                                    for(int y=0;y<=1;y++){
                                        int val=f[i-1][j-(r-l+1)][p][q][x][y];
                                        if(tf<val){
                                            tf=val;
                                            tg=(state){i-1,j-(r-l+1),p,q,x,y};
                                        }
                                }
                        for(int p=l;p<=r;p++)
                            tf+=a[i][p];
                    }
                }
    int res=0;
    state fin;
    for(int i=1;i<=n;i++)
        for(int l=1;l<=m;l++)
            for(int r=1;r<=m;r++)
                for(int x=0;x<=1;x++)
                    for(int y=0;y<=1;y++){
                        int val=f[i][k][l][r][x][y];
                        if(res<val){
                            res=val;
                            fin=(state){i,k,l,r,x,y};
                        }
                    }
    printf("Oil : %d\n",res);
    while(fin.j){
        for(int i=fin.l;i<=fin.r;i++)
            printf("%d %d\n",fin.i,i);
        fin=g[fin.i][fin.j][fin.l][fin.r][fin.x][fin.y];
    }
    return 0;
}