Leetcode Blind 75 | Find minimum & Search in rotated sorted array

1. Find Minimum in Rotated Sorted Array
 

• 给定一个数组经过n次旋转后找出最小值，数组预先升序排

  

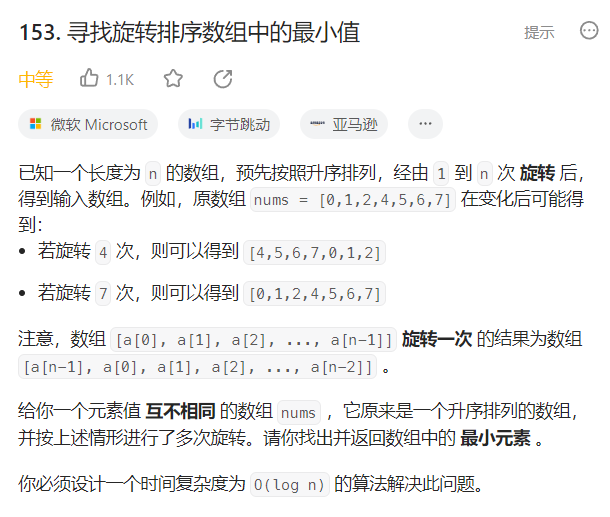
a. 思路

• 切入：时间复杂度 O(logn)-->二分法：左右两端、中间指针-->涉及比较
• 数组特性：即使数组被旋转，它的两个子数组（旋转点分隔的两部分）仍然是升序的--->决定比较结果，指针移动方向
• 核心：比较中间元素与左/右端点的大小关系 （根据从左往右的习性，就比较左端点好了）

  

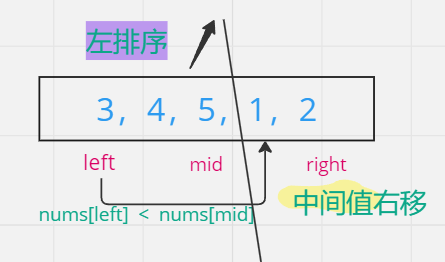
• • 如果 [mid] > [left]，

• • • 说明中间元素与其前面的元素是按照升序排列的，是左排序的一部分，那么下一步就是往右边找最小值

• • 如果 [mid] < [left]，

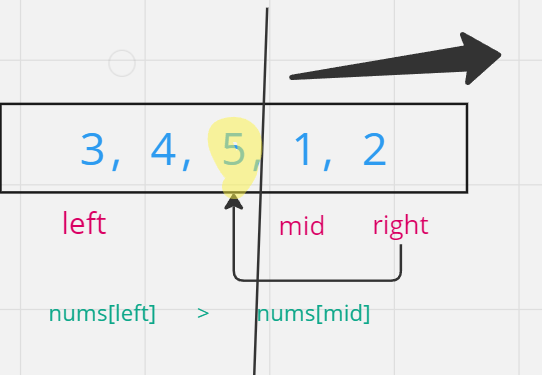
• • • 意味中间指针属于右排序，越往右越大，我们不确定中间指针是否位于右排序最左，所以指针往左移动

      

• 边缘：

• • 数组存在重复元素（题干排除）
  • 数组未经旋转/完全升序时，最左即最小值---while循环优化：在二分查找前检查数组是否已经升序-->if nums[l] < nums[r]，减少不必要的二分查找迭代

b. Coding

输入：给定数组nums

输出：最小值 res

变量：

最小值res

二分法下标：left,right,mid

算法/语句：

1. 初始化结果和下标变量
   1. 初始化结果为数组第一个元素，在完全升序情况下，第一个即最小值 res=nums[0]
   2. 初始化下标表示搜索范围 left, right = 0, len(nums)-1
2. while循环移动下标直到返回结果
   1. 跳出循环条件：left > right
   2. 检查数组是否已是升序
      1. if 语句将最小值res与现搜索范围内的最左比较
      2. bresk 退出循环，返回结果
   3. 二分查找
      1. 计算中间位置 mid
      2. 更新res
         1. 为了代码的可读性和逻辑清晰，我们倾向于在可能改变变量值之前立即更新所需要的值
         2. 把此语句放在 if-else后面不会影响结果，因为mid位置不变，left和right更新不会影响min()的搜查范围
      3. 比较中间值和左断电大小关系
         1. if
         2. else
3. return res

class Solution(object):
    def findMin(self, nums):
        res = nums[0]
        left, right = 0, len(nums)-1

        while left <= right:
            if nums[left]<nums[right]:
                res = min(nums[left], res)
                break
            
            mid = (left+right)//2
            res = min(res,nums[mid])
            if nums[mid]>=nums[left]:
                left = mid+1
            else:
                right = mid-1
        return res

2. Search in rotated sorted array

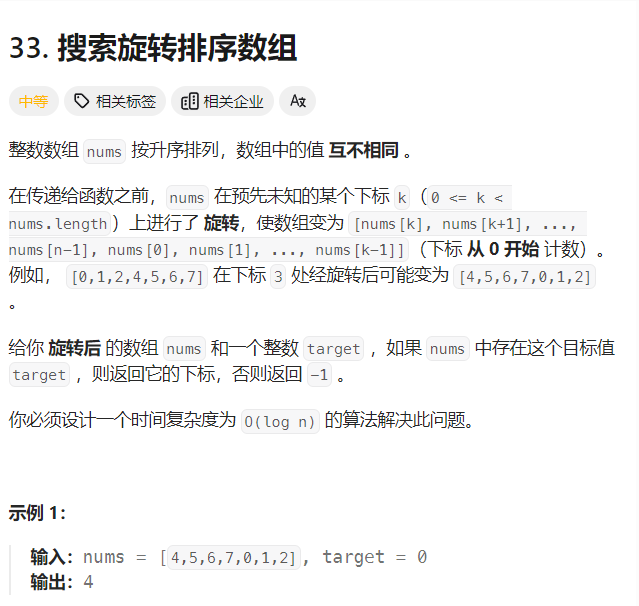
a. 思路

旋转数组可以看作是分段函数的简化版本，其中每一段都是有序的

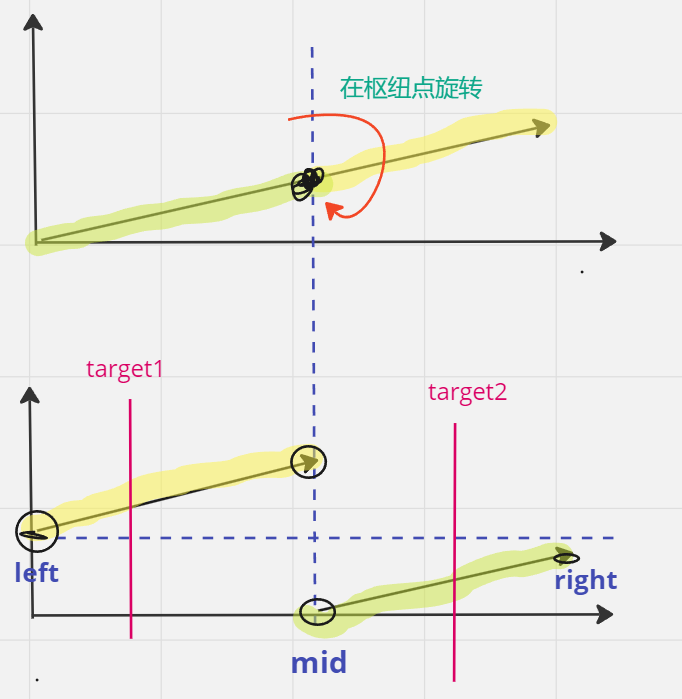
【mid可能在上也可能在下】

如果数组在枢纽点旋转，左端点>右端点，中间是断点、两个搜索区间-->二分法：

传统的二分搜索是在完全排序的数组中进行的，但在这个问题中，可以通过比较中间元素和区间端点来判断中间元素属于哪个排序的子数组

由此推彼，在未知旋转数组中，所有需要被确定的都是此图已有的特点：

1. 确定中点：把数组分为两个部分的断点，但除了（left+right）/2外，不能可视化，所以只能从子数组升序这个特点入手
2. 确定哪个子数是有序的：比较中点和端点
   1. nums[left] <= nums[mid]--->左排序
   2. nums[mid] < nums[right]--->右排序
3. 确定target所在区间&调整搜索边界链接
   1. 左分段

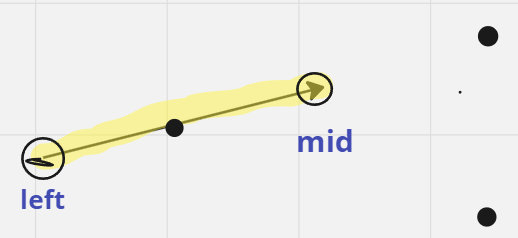
1. 1. 1. target在黄线外：target>nums[mid] 或 target< nums[left]：mid+1
      2. target在黄线上：nums[left] < target < nums[mid] : mid-1

b. 断点： target == mid

c. 右分段

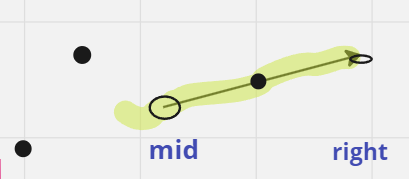
1. 1. 1. target在绿线外：target < nums[mid] 或 target>nums[right]：mid-1
      2. target 在绿线上：nums[mid] <target < nums[right]：mid+1

b. Coding

输入：给定数组nums

输出：target下标

变量：

1. 1. 二分法：left right mid
   2. 目标值target
   3. 给定数组 nums

算法/语句

• 初始化二分法变量：lefy right
  • mid 随着left right 的变化而变化，所以在循环内部定义

• while 循环
  • 判断条件：left <= right
    • 当 left 和 right 相遇时，仍然会执行循环体内的代码，在循环内部检查 mid 是否等于 target
  • mid 定义
    • 断点
      • target == nums[mid]
    • 左分段
      • 黄线内外
    • 右分段
      • 绿线内外
• 循环完了还没找到 return -1

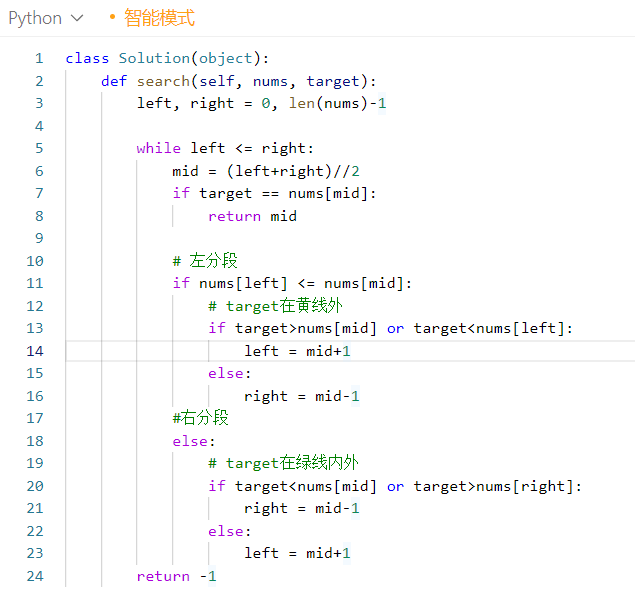
c. 错误

每次确定搜索范围，都是靠移动左右两端left&right，不是左分段leftleft，右分段rightright，不要被语言迷惑

d. 优化