学习基于Java面向对象的标准粒子群算法
前言
大学时,曾参与过数学建模集训与竞赛,对于许多模型算法影响深刻。最近回首大学时期的相关代码,突然有兴致重新梳理实现,整体思路按照数学建模的四大模型:优化,分类,预测,评价模型整理。
说到优化模型,就想到最优化问题,提到最优化问题,就想到智能算法,看到智能算法,就联想到群智能算法,群智能算法中,最早也是最出名的就是粒子群算法,今天就让我们来学习下粒子群算法。
粒子群算法
简要介绍
粒子群优化(Particle Swarm Optimization,PSO),又称微粒群算法,是由J. Kennedy和R. C. Eberhart等于1995年开发的一种演化计算技术,来源于对一个简化社会模型的模拟。其中“群(swarm)”来源于微粒群匹配M. M. Millonas在开发应用于人工生命(artificial life)的模型时所提出的群体智能的5个基本原则。“粒子(particle)”是一个折衷的选择,因为既需要将群体中的成员描述为没有质量、没有体积的,同时也需要描述它的速度和加速状态。PSO算法最初是为了图形化的模拟鸟群优美而不可预测的运动。而通过对动物社会行为的观察,发现在群体中对信息的社会共享提供一个演化的优势,并以此作为开发算法的基础。通过加入近邻的速度匹配、并考虑了多维搜索和根据距离的加速,形成了PSO的最初版本。之后引入了惯性权重w来更好的控制开发(exploitation)和探索(exploration),形成了标准版本。为了提高粒群算法的性能和实用性,中山大学、(英国)格拉斯哥大学等又开发了自适应(Adaptive PSO)版本和离散(discrete)版本。
上述描述出自百度百科《粒子群优化》,其中有描述到群体智能的5个基本原则,这五个原则如下:
- 邻近原则(ProximityPrinciple):群体应该能够执行简单的空间和时间运算。
- 质量原则(Quality Principle):群体应该能感受到周围环境中质量因素的变化,并对其产生响应。
- 反应多样性原则(Principle of Diverse Response):群体不应将自己获取资源的途径限制在狭窄的范围之内。
- 稳定性原则(Principle ofStability):群体不应随着环境的每一次变化而改变自己的行为模式。
- 适应性原则(Principle ofAdaptability):当改变行为模式带来的回报是值得的时候,群体应该改变其行为模式。
通俗点以鸟群举例说明就是:一群鸟在一定范围内搜索食物,他们不知道食物的具体位置,但能知道自己和其他鸟当前距离食物的远近关系,最简单有效的搜索方式就是逐步逼近当前最接近食物的那只鸟,在这过程中继续搜索食物,更新并传递自己的信息至其他鸟,鸟群协作搜索,最终整个鸟群聚集在食物附近,即找到最优解。
算法描述
假设 种群的粒子数量用n表示,问题的维度用d表示,则该种群的数学表达形式为n*d的向量。
算法涉及的符号说明如下
| 符号 | 说明 |
|---|---|
| x | 粒子的位置 |
| rand() | 0·1的随机数 |
| top | 解空间的上界 |
| down | 解空间的下界 |
| v | 粒子的速度 |
| zero | 零值 |
| pbest | 粒子的历史最优解 |
| gbest | 种群的历史最优解 |
| wMax | 速度的最大权重 |
| wMin | 速度的最小权重 |
| w | 当前速度权重 |
| tMax | 最大迭代次数 |
| t | 当前迭代次数 |
| c1 | 自身的学习因子 |
| c2 | 种群的学习因子 |
初始化阶段
每个粒子位置初始化可以用下述公式表示
x
=
r
a
n
d
(
)
∗
(
t
o
p
−
d
o
w
n
)
+
d
o
w
n
x=rand()*(top-down)+down
x=rand()∗(top−down)+down
速度初始化为零
v
=
z
e
r
o
v=zero
v=zero
同时,计算每个粒子的适应度值,计算自身的历史最优解与种群最优解
p
b
e
s
t
=
f
(
x
)
pbest=f(x)
pbest=f(x)
g
b
e
s
t
=
max
p
b
e
s
t
gbest=\mathop{\max}\limits_{pbest}
gbest=pbestmax
迭代阶段
根据最大迭代次数,从t=0开始自增迭代,每个粒子,根据下述速度更新公式更新自身速度
w
=
w
M
a
x
−
t
∗
(
w
M
a
x
−
w
M
i
n
)
/
t
M
a
x
w= wMax-t*(wMax-wMin)/tMax
w=wMax−t∗(wMax−wMin)/tMax
v
=
w
∗
v
+
c
1
∗
r
a
n
d
(
)
∗
(
p
b
e
s
t
−
x
)
+
c
1
∗
r
a
n
d
(
)
∗
(
g
b
e
s
t
−
x
)
v=w*v+c1*rand()*(pbest-x)+c1*rand()*(gbest-x)
v=w∗v+c1∗rand()∗(pbest−x)+c1∗rand()∗(gbest−x)
再根据位置更新公式更新位置
x
=
x
+
v
x=x+v
x=x+v
校验边界值,防止粒子跑出解空间
x
=
{
t
o
p
x
>
=
t
o
p
x
d
o
w
n
<
x
<
t
o
p
d
o
w
n
x
<
=
d
o
w
n
x=\begin{cases} top & x>=top \\ x & down<x<top \\ down & x<=down \end{cases}
x=⎩
⎨
⎧topxdownx>=topdown<x<topx<=down
再更新自身的历史最优解
p
b
e
s
t
=
{
f
(
x
)
f
(
x
)
>
p
b
e
s
t
p
b
e
s
t
f
(
x
)
<
=
p
b
e
s
t
pbest=\begin{cases} f(x) & f(x)>pbest \\ pbest & f(x)<=pbest \end{cases}
pbest={f(x)pbestf(x)>pbestf(x)<=pbest
接着更新种群的历史最优解
g
b
e
s
t
=
{
max
p
b
e
s
t
max
p
b
e
s
t
>
g
b
e
s
t
g
b
e
s
t
max
p
b
e
s
t
<
=
p
b
e
s
t
gbest=\begin{cases} \mathop{\max}\limits_{pbest} & \mathop{\max}\limits_{pbest}>gbest \\ gbest & \mathop{\max}\limits_{pbest}<=pbest \end{cases}
gbest=⎩
⎨
⎧pbestmaxgbestpbestmax>gbestpbestmax<=pbest
当达到最大迭代次数时,算法结束,输出最优解gbest以及对应的x
Java
对于粒子群算法,网上大都是以MATLAB,Python 等专业数学计算库语言,以面向过程方式编程实现。而Java是一门面向对象的编程语言,PSO算法中的粒子,粒子群,符合对象概念,适应度函数也符合接口概念,故用面向对象思想实现该算法也合适。
根据粒子群算法的算法描述,大体可以抽象出如下对象
Particle:粒子对象,其自身有四个属性与六个方法
- position:位置属性
- velocity:速度属性
- best:最优值属性
- bestFit:最优值的解属性
- positionInit:位置初始化方法
- velocityInit:速度初始化方法
- velocityUpdate:速度更新方法
- positionUpdate:位置更新方法
- getBest:获取最优值方法
- getBestFit:获取最优值的解方法

ParticleSwarm:粒子群对象,其自身有12个属性和两个方法
- particles:粒子列表属性
- nPop:粒子数量属性
- dim:问题维度属性
- positionUp:解空间上界属性
- positionDown:解空间下界属性
- wMax:速度最大权重属性
- wMin:速度最小权重属性
- c1:粒子学习因子属性
- c2:种群学习因子属性
- maxIt:最大迭代次数属性
- fitnessFunction:适应度函数属性
- gBestParticle:种群最优解属性
- initParticles:种群初始化
- iterativeParticles:种群迭代

最后,是适应度函数接口,主要用于根据具体的问题,实现具体的方法

JavaFx
JavaFX 是一个开源的下一代客户端应用程序平台,适用于基于 Java 构建的桌面、移动和嵌入式系统。是一个现代、高效且功能齐全的工具包,当然也就可以绘制图表。本人研究JavaFx不多,这里也就不过多赘述。有兴趣研究的童靴,可以点击FXDocs深入学习。
javaFx应用顶层是场景,场景是有节点的分层数,表示应用用户界面的所有可见元素,可以处理输入,也可以处理数据输出。其结构如下:
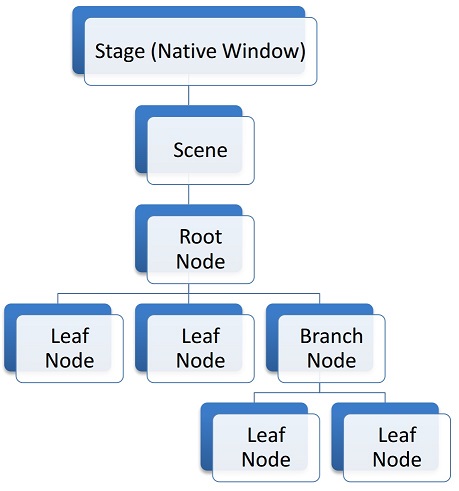
对于可视化算法结果,最好的方式就是用图表展示,这里常见的是折线图,JavaFx也有对于UI控件: LineChart
示例
对于一个7维的sphere函数
y
=
∑
n
=
1
7
x
n
2
y=\sum_{n=1}^7x_n^2
y=n=1∑7xn2
(
−
500
<
x
n
<
500
)
(-500<x_n<500)
(−500<xn<500)
求其最小值,一眼便知道其最小值为0,解为(0,0,0,0,0,0,0)
我们假设 粒子群总数为50 ,速度权重在0.9-0.6之间,学习因子c1=c2=2,最大迭代次数200
多次执行粒子群算法,算法运行图如下:

后记
本期的内容对应的代码库:swarmIntelligence
从运行结果图,粒子群算法前期可快速收敛,但在高维问题中,后期收敛慢,容易陷入局部最优解中,因此,标准粒子群算法有很多改进算法,后面我们再进一步研究学习改进的粒子群算法。




















 6530
6530

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








