swift算法之排序：（五）归并排序

1、概述

归并排序是建立在归并操作上的一种有效的排序研发，该算法主要是采用分治法（divide and conquer）的思想。

在归并排序中，需要将排序的数组进行拆分，将其拆分的足够小，当拆分的数组中只有一个元素时，则拆分的数组是有效的，然后将这些有序的数组进行两两合并，并在合并的过程中进行比较，合并生成的新数组仍然是有序的，然后再次将合并的有序数组进行合并，重复这个过程，直到整个数组都是有序的为止。

2、算法原理

思想：分而治之，即将一个大问题分解成较小的问题并解决他们，可以分为 先拆分 和 后合并，即 拆分+合并

步骤：

1）将数字放在未排序的堆中

2）将堆分成两部分，即两个未排序的数字堆

3）继续分裂 两个未排序的数字堆，知道不能分裂为止，最后，你将拥有 n 个堆，每个堆中有一个数字

4）通过顺序配对，开始合并堆，在每次合并期间，将内容按排序顺序排列

 

3、举例

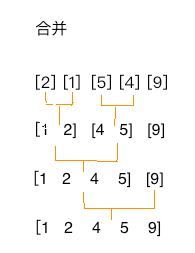
对 [2, 1, 5, 4, 9] 排序

1）将数组元素拆分成5个单独的数组，每个数组包含一个元素

2）将拆分的数组两两合并，并排序，直到整个数组都是有序为止

 

4、算法实现

1）自上而下的递归实现

拆分+合并

func mergeSort(_ array: [Int])->[Int]{
        //1、如果数组为空或包含单个元素，则无法将其拆分为更小的部分，返回数组就行
        guard array.count > 1 else{
            return array
        }
        //2、找到中间索引
        let middleIndex = array.count/2
        
        //3、使用上一步中的中间索引，递归的分割数组的左侧
        let leftArray = mergeSort(Array(array[0..<middleIndex]))
        
        //4、递归的分割数组的右侧
        let rightArray = mergeSort(Array(array[middleIndex..<array.count]))
        
        //5、将所有值合并在一起，确保它始终排序
        return merge(leftArray, rightArray)
    }
    //合并算法
    private func merge(_ leftPile : [Int], _ rightPile : [Int])->[Int]{
        //1、合并时需要两个索引来跟踪两个数组的进度
        var leftIndex = 0
        var rightIndex = 0
        
        //2、合并后的数组，目前时空的，需要在下面的操作中添加其他数组中的元素构建
        var orderedPile = [Int]()
        
        //3、while循环将比较左侧和右侧的元素，并添加到orderpile。同时确保结果保持有序
        while leftIndex<leftPile.count && rightIndex<rightPile.count {
            if leftPile[leftIndex] < rightPile[rightIndex]{
                orderedPile.append(leftPile[leftIndex])
                leftIndex += 1
            }else if leftPile[leftIndex]>rightPile[rightIndex]{
                orderedPile.append(rightPile[rightIndex])
                rightIndex += 1
            }else{
                orderedPile.append(leftPile[leftIndex])
                leftIndex += 1
                orderedPile.append(rightPile[rightIndex])
                rightIndex += 1
            }
        }
        
        //4、如果前一个while循环完成，意味着left/right中的一个内容已经完全合并到orderpile中，不需要再比较，只需要依次添加剩下的数组的剩余元素
        while leftIndex < leftPile.count {
            orderedPile.append(leftPile[leftIndex])
            leftIndex += 1
        }
        
        while rightIndex < rightPile.count {
            orderedPile.append(rightPile[rightIndex])
            rightIndex += 1
        }
        
        return orderedPile
    }

2）自上而下的非递归实现

   func mergeSort1(_ array: [Int])->[Int]{
        //1、如果数组为空或包含单个元素，则无法将其拆分为更小的部分，返回数组就行
        guard array.count > 1 else{
            return array
        }
        
        //2、将数组中的每一个元素放入一个数组中
        var tampArr : [[Int]] = []
        for item in array {
            var subArr : [Int] = []
            subArr.append(item)
            tampArr.append(subArr)
        }
        
        //3、对数组中的数组进行合并，直到合并完成为止
        while tampArr.count != 1 {
            print(tampArr)
            var i = 0
            while i < tampArr.count-1 {
                tampArr[i] = merge(tampArr[i], tampArr[i+1])
                tampArr.remove(at: i+1)
                i += 1
            }
        }
        return tampArr.first!
    }

3）自下而上的迭代实现

排序数组时，跳过拆分步骤并立即开始合并各个数组元素

func mergeSortBottomUp<T>(_ array : [T], _ isOrderedBefore:(T, T)->Bool)->[T]{
        let n = array.count
        
        //1、归并排序需要一个临时工作数组，因为不能再原数组合并同时又覆盖原有内容---使用两个数组，将使用d的值在他们之前切换，它是0/1，数组 z[d] 用于读，数组 z[1-d] 用于写，称为双缓冲
        var z = [array, array]
        var d = 0
        
        //2、自下而上与x自上而下工作方式相同，都是先合并每个元素的小堆，在合并每个堆两个元素---堆的大小由 width 给出，width初始是1，但在每次迭代结束时，width *2，所以外循环确定合并的堆的大小
        var width = 1
        while width < n {
            var i = 0
            //3、内循环穿过堆并将每对堆合并成一个较大堆，结果写入z[1-d]给出的数组中
            while i < n{
                var j = i
                var left = i
                var right = i+width
                
                let lmax = min(left+width, n)
                let rmax = min(right+width, n)
                
                //4、与自下而上逻辑相同，区别在于自上而下使用双缓冲，从z[d]读 并写入 z[1-d],还是用isOrderedBefore函数来比较元素，是通用的
                while left < lmax && right < rmax{
                    if isOrderedBefore(z[d][left], z[d][right]) {
                        z[1-d][j] = z[d][left]
                        left += 1
                    }else{
                        z[1-d][j] = z[d][right]
                        right += 1
                    }
                    j += 1
                }
                while left<lmax {
                    z[1-d][j] = z[d][left]
                    j += 1
                    left += 1
                }
                while right < rmax {
                    z[1-d][j] = z[d][right]
                    j += 1
                    right += 1
                }
                i += width*2
            }
            width *= 2
            
            //5、z[d]的大小width 的堆已经合并为数组z[1-d]中更大的大小width*2，这里 交换活动数组，方便在下一步中我们从刚刚创建的新堆中读取
            d = 1-d
        }
        return z[d]
    }

4）调用

        var array5 = [2, 1, 5, 4, 9]
        //自上而下-递归
        //array5 = mergeSort(array5)
        //自上而下-非递归
        array5 = SortSummary.mergeSort1(array5)
        //自下而上-迭代
        print(array5)
        array5 = mergeSortBottomUp(array5, <)


运行结果：

[1, 2, 4, 5, 9]
[1, 2, 4, 5, 9] 

5、时间复杂度

最好、最差和平均情况的时间复杂度将始终为 O(nlogn)。

 

github代码

注：排序的具体实现代码在 SortSummary.swift 文件里 调用是在 ViewController.swift