算法基础-回归

回归

线性回归

假设误差项服从高斯分布，则其概率密度可知，可以写出其似然函数，又误差项ε等于y-θx,则L（θ）如上图

取对数再求导

岭回归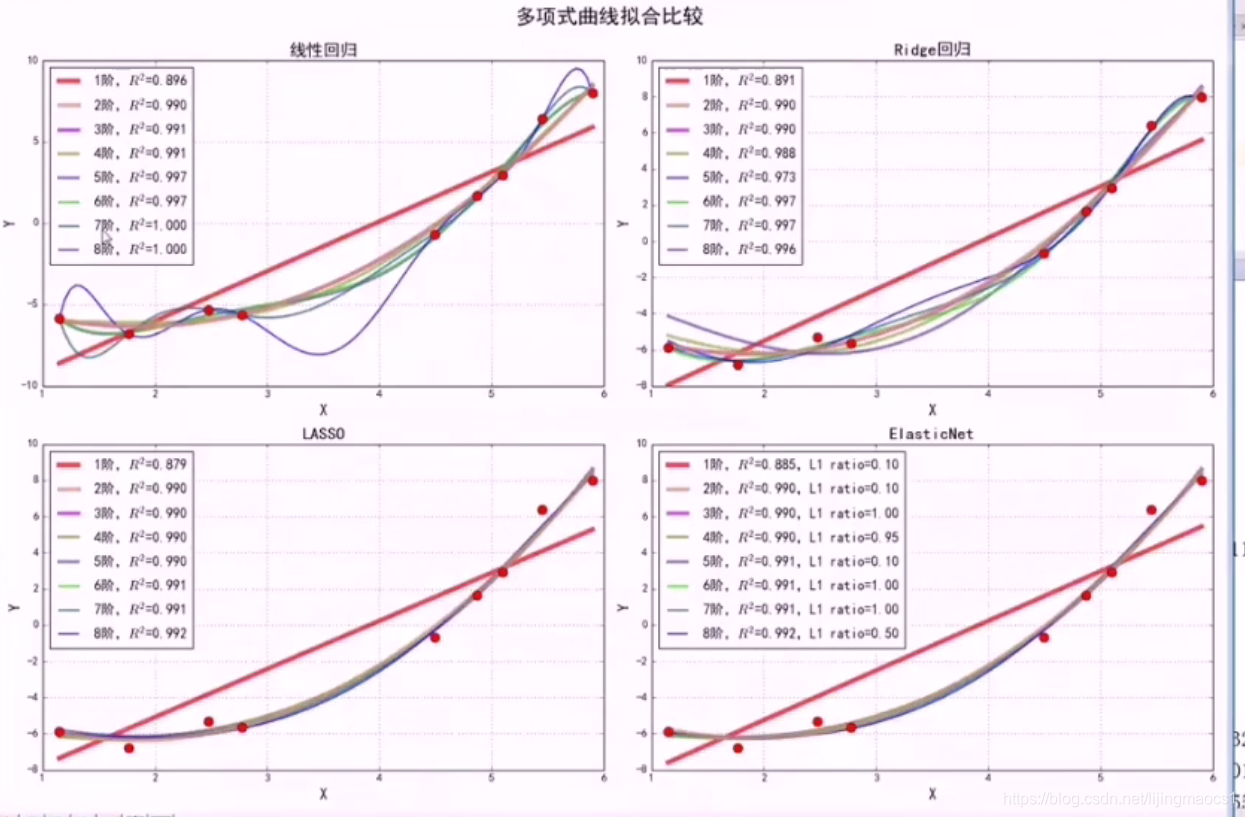

线性回归若阶数越高，与样本点拟合的越好，也越容易过拟合。系数的值也越大，不稳定性越大，为了防止过拟合，增加约束项防止参数值太大。LL2是希望seta的平方不要太大，L1正则是seta的绝对值不要太大。

L2正则项是seta的平方，L1正则是seta的绝对值，线性回归用L2正则，叫岭回归，线性回归用L1正则叫lasso回归。

Lasso一定程度上有特征选择的功效(高阶的系数接近于0，等同于特征选择)，L2正则性能更好，Elastic Net 结合了L1、L2

梯度下降

https://blog.youkuaiyun.com/lijingmaocs1/article/details/104664818

实际中常用的

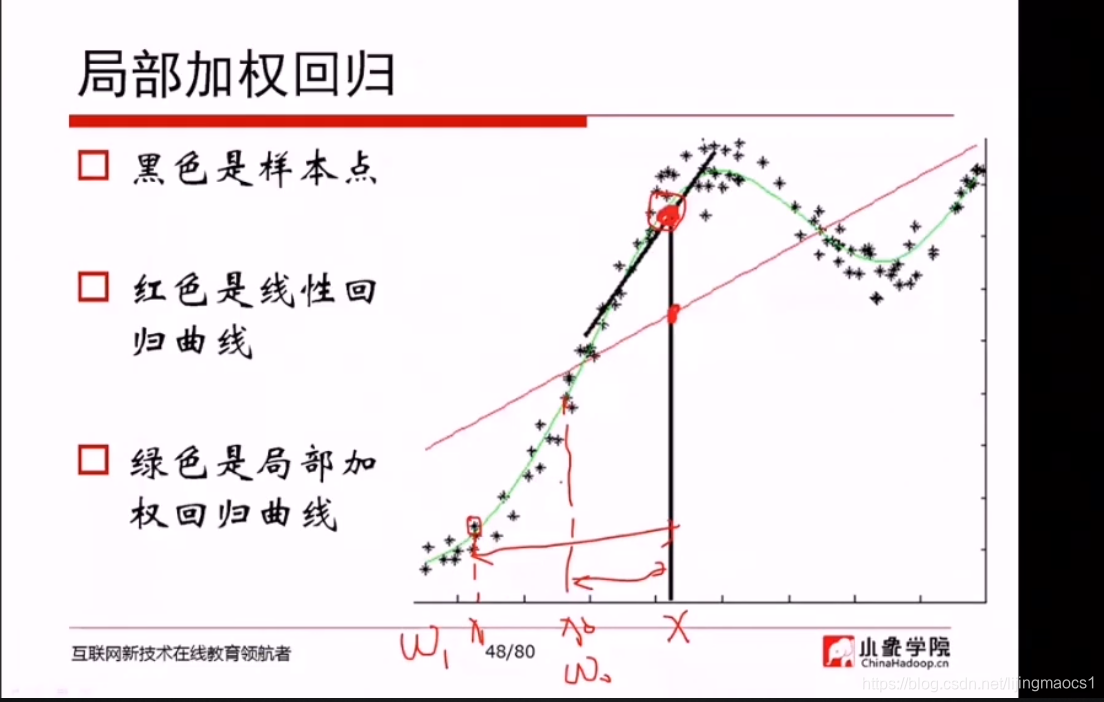
局部加权回归

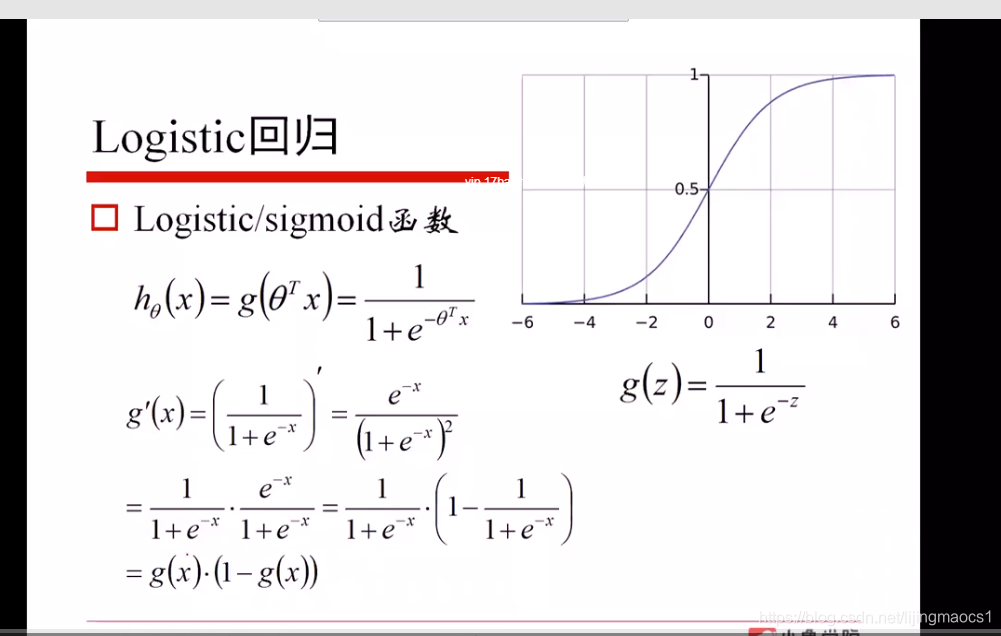
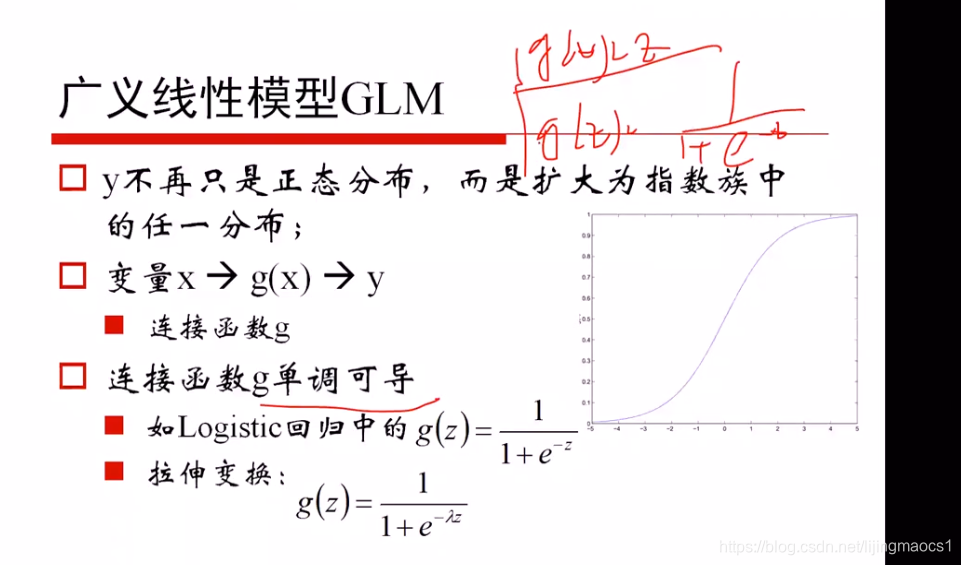
逻辑回归

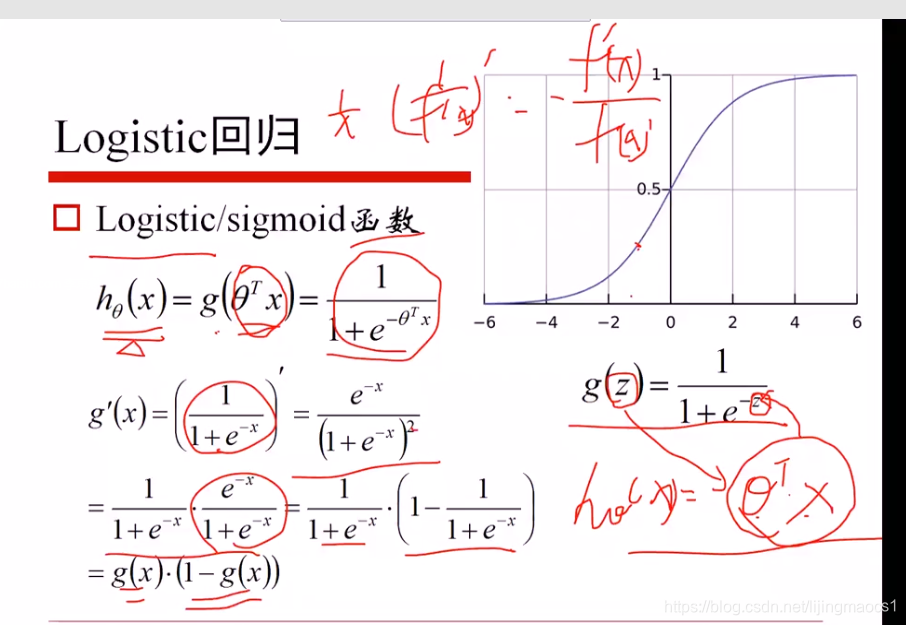
上面为似然函数，样本服从二项分布


逻辑回归样本服从二项分布，线性回归样本服从高斯分布，都属于指数族分布，所以他们的参数更新的形式都是一样的

logistic损失函数

fi是θT*X




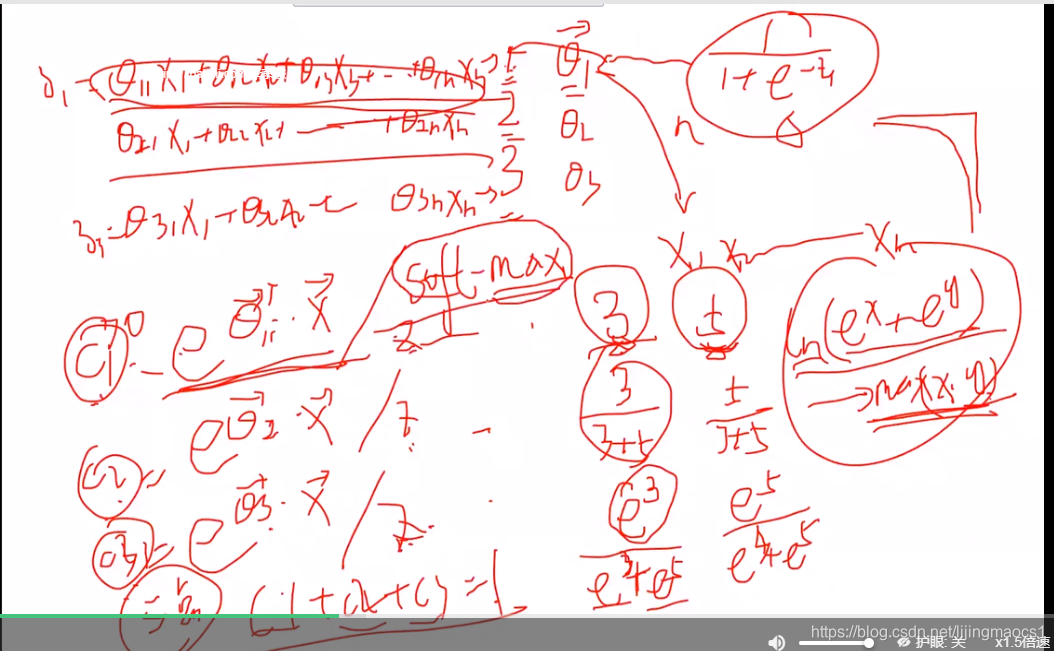
soft-max回归思想，处理多分类问题, 计算属于1/2/3种类别时，分别有3组参数seta1、seta2、seta3，分别与x相乘后得到一个数α1,α2,α3，再用a1/a1+a2+a3，a2/a1+a2+a3，a3/a1+a2+a3,近似理解为属于该类别的概率；
谁的概率大就属于哪个类别。ps 这里是变形为e的次方的形式