冒泡排序、选择排序、快速排序
冒泡排序
冒泡排序的思想在于,不断地将当前元素与后一个元素进行比较,如果当前元素较小,则调换当前元素与后一个元素的位置,否则保持不变;假设需要排序的元素一共有n个,从第一个元素开始,对后续的(n-2)元素进行上述比较,最终的排序结果中,最后的元素是最大值。
def bubble_sort(alist):
n = len(alist)
for j in range(n-1):
for i in range(n-1-j):
if alist[i] > alist[i+1]:
alist[i],alist[i+1] = alist[i+1],alist[i]
选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
算法步骤
1.首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
2.再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3.重复第二步,直到所有元素均排序完毕。
def select_sort(alist):
n = len(alist)
for j in range(n-1):
min_index = j
for i in range(j+1, n):
if alist[min_index] > alist[i]:
min_index = i
alist[j], alist[min_index] = alist[min_index], alist[j]
快速排序
算法思想
快速排序的核心思想在于:首先在这个序列中随便找一个数作为基准数,然后将这个序列中所有比基准数大的数放在该数字的右边,比基准数小的数放在该数字的左边。第一轮排序结束之后,再分别对已经好的基准书左边(比基准数小)和基准书右边(比基准书大)的数字序列重复上述操作,用递归形式即可实现快速排序,完成对整个序列的排序。
算法步骤
为了清晰地展示快速排序的原理,这里使用一个例子来具体说明快速排序算法排序的过程。
假定现在要对数字序列 [4, 2, 7,8, 0,1, 5,23] 进行快速排序。
我们假设最左边的编号为i,最左边的编号为j,不失一般性,假定以4作为基准进行排序(每一次总总是让j先出发,向左移动,再让i出发,向右移动)。
(一)第一轮排序
j向左出发寻找第一个小于4的数,遇到1的时候停下来;i向右出发寻找第一个大于4的数,遇到7的时候停下来,交换两者的位置,数字序列变为
[4,2,1,8,0,7,5,23]
接下继续让j向左移动,寻找第二个小于4的数,遇到0的时候停下来;让i向右移动,寻找第二个大于4的数,遇到8的时候停下来,交换两者的位置,数字序列变为
[4,2,1,0,8,7,5,23]
此时发现i与j相遇了,第一轮排序结束,调换4和0的位置,数字序列变为
[0,2,1,4,8,7,5,23],
所有小于4的数字都在4的左边,所有大于4的数字都在4的右边。
(二)第二轮排序
分别对4左边和4右边的数字序列进行排序处理,首先对4左边的数字序列[0,2,1]排序。
以第一个数字0为基准,j向左出发寻找第一个小于0的数,i向右出发寻找第一个大于0的数,遇到0的时候停下来,如果找到就交换两者的位置,否则不变。数字序列变为[0,2,1],所有小于0的数字都在0的左边,所有大于0的数字都在0的右边。
再对4右边的数字序列[8, 7,5,23]排序。
以第一个数字8为基准,j向左出发寻找第一个小于8的数,遇到5的时候停下来;i向右出发寻找第一个大于8的数,如果找到就交换两者的位置,同时保证i小于j,那么数字序列变为[5,7,8,23]。所有小于8的数字都在8的左边,所有大于8的数字都在8的右边。
总体数字序列变为[0,2,1,4,5,7,8,23]。
(三)第三轮排序
好了动手算一算,类似第一和第二轮的排序方法,对0右边的数字序列进行排序,得到[0,1,2];对8左边的数字序列进行排序,得到[5,7,8,23]。第三轮排序结束。
得到最终的排序结果为
[0,1,2,4,5,7,8,23]。
快排过程结束。
def quick_sort(alist, first, last):
if first >= last:
return
mid_value = alist[first]
low = first
high = last
while low < high:
# high 左移#
while low < high and alist[high] >= mid_value:
high -= 1
alist[low] = alist[high]
while low< high and alist[low] < mid_value:
low += 1
alist[high] = alist[low]
#从循环退出时,low == high#
alist[low] = mid_value
#左边#
quick_sort(alist, first, low-1)
#右边
quick_sort(alist, low+1 , last)
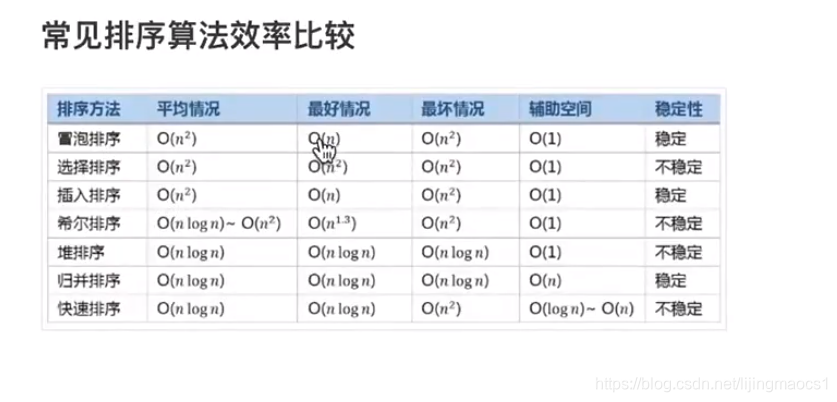
 经典排序算法详解
经典排序算法详解




















 865
865

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








