迪杰斯特拉算法简介
迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
迪杰斯特拉算法原理
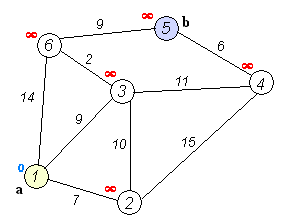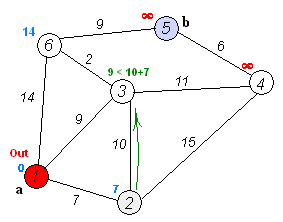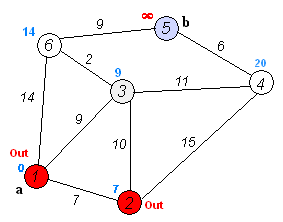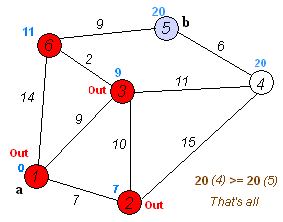
1.首先,引入一个辅助向量D,它的每个分量 D 表示当前所找到的
Dijkstra算法运行动画过程
Dijkstra算法运行动画过程
从起始点 (即源点 )到其它每个顶点 的长度。
例如,D[3] = 2表示从起始点到顶点3的路径相对最小长度为2。这里强调相对就是说在算法执行过程中D的值是在不断逼近最终结果但在过程中不一定就等于长度。[1]
2.D的初始状态为:若从 到 有弧(即从 到 存在连接边),则D 为弧上的权值(即为从 到 的边的权值);否则置D 为∞。
显然,长度为 D = Min{ D | ∈V } 的路径就是从 出发到顶点 的长度最短的一条路径,此路径为( )。
3.那么,下一条长度次短的是哪一条呢?也就是找到从源点 到下一个顶点的最短路径长度所对应的顶点,且这条最短路径长度仅次于从源点 到顶点 的最短路径长度。
假设该次短路径的终点是 ,则可想而知,这条路径要么是( ),或者是( )。它的长度或者是从 到 的弧上的权值,或者是D 加上从 到 的弧上的权值。
4.一般情况下,假设S为已求得的从源点 出发的最短路径长度的顶点的集合,则可证明:下一条次最短路径(设其终点为 )要么是弧( ),或者是从源点 出发的中间只经过S中的顶点而最后到达顶点 的路径。
因此,下一条长度次短的的最短路径长度必是D = Min{ D | ∈V-S },其中D 要么是弧( )上的权值,或者是D ( ∈S)和弧( , )上的权值之和。
算法描述如下:
1)令arcs表示弧上的权值。若弧不存在,则置arcs为∞(在本程序中为MAXCOST)。S为已找到的从 出发的的终点的集合,初始状态为空集。那么,从 出发到图上其余各顶点 可能达到的长度的初值为D=arcs[Locate Vex(G, )], ∈V;
2)选择 ,使得D =Min{ D | ∈V-S } ;
3)修改从 出发的到集合V-S中任一顶点 的最短路径长度。







 本文详细介绍了迪杰斯特拉算法,一种用于解决有向图中最短路径问题的经典算法。文章通过逐步解析算法原理,解释了如何从一个顶点出发,计算到其他所有顶点的最短距离。
本文详细介绍了迪杰斯特拉算法,一种用于解决有向图中最短路径问题的经典算法。文章通过逐步解析算法原理,解释了如何从一个顶点出发,计算到其他所有顶点的最短距离。
















 4874
4874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








