Simulink搭建C语言仿真模型
1、 在library库中查找S-Function Builder模块,拖入到空白区;
2、 该模块即为C语言代码模块,双击该模块,在Initialization栏,设置sample mode为离散采样,采样时间间隔Sample time value为控制周期,本示例设置为0.0001s,即10kHz控制频率;
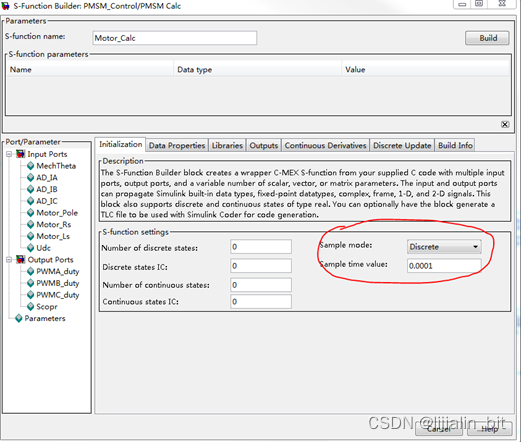
3、 在Data Properties栏添加模块的输入输出端口,设置端口名称,为了方便理解,本示例将输入输出端口都设置成为1-D维度(单一维度),为了尽量贴近单片机的运行效果,Data type attributes将数据类型设置为single;
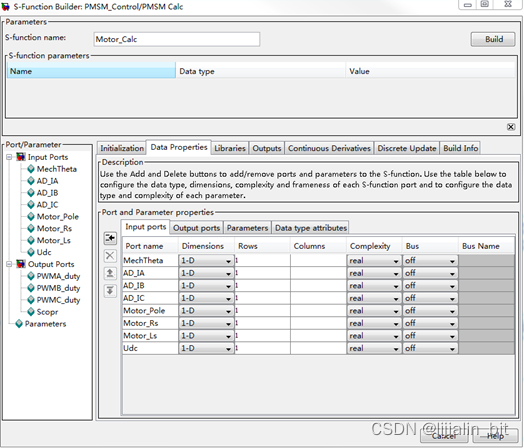
4、 在libraries栏添加仿真需要使用的.h文件和.c文件,注意文件中包括注释都不要出现中文字符,否则可能会报错;
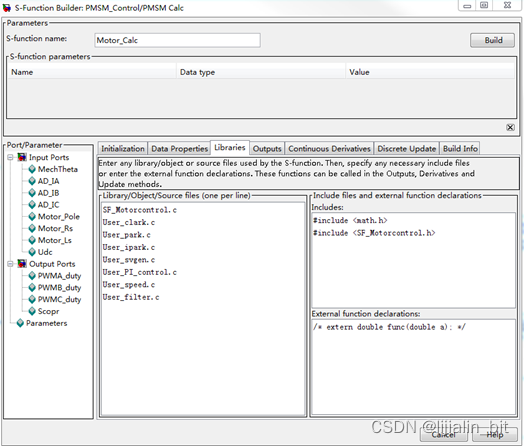
5、 在Outputs栏编写输入输出端口与执行代码,这里可以将仿真的C代码精简为一个函数,在函数中编写算法,可以简化本栏的内容,将输入信号赋值给内部变量,将文件输出变量赋值为输出端口,注意,输入输出端口都是指针形式,要以数组形式操作;
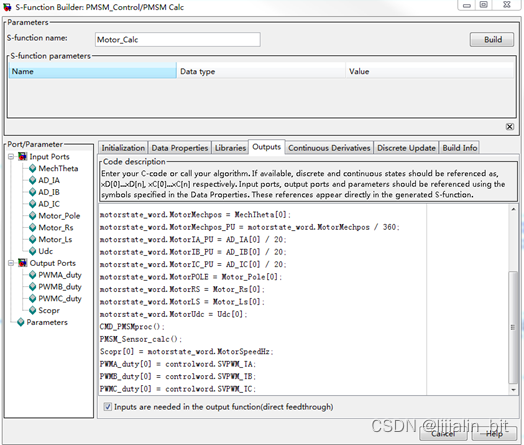





 本文详细介绍了如何在Simulink中使用C语言构建仿真模型,涉及S-FunctionBuilder模块的配置、数据端口设置、C代码编写及常见错误处理,包括采样频率、数据类型和初始化问题。
本文详细介绍了如何在Simulink中使用C语言构建仿真模型,涉及S-FunctionBuilder模块的配置、数据端口设置、C代码编写及常见错误处理,包括采样频率、数据类型和初始化问题。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








