695.岛屿的最大面积——DFS详解+网格类题目通用解法

最新推荐文章于 2024-05-04 20:36:03 发布

lightupworld

最新推荐文章于 2024-05-04 20:36:03 发布

阅读量388

点赞数

CC 4.0 BY-SA版权

分类专栏： # 经典题型

本文链接：https://blog.youkuaiyun.com/lightupworld/article/details/107793429

经典题型专栏收录该内容

9 篇文章

订阅专栏

本文详细解析了如何使用深度优先搜索（DFS）解决岛屿最大面积的问题，介绍了DFS在处理网格类题目中的应用。通过标记已访问的方格避免重复遍历，确保了算法的正确性。提供了简洁的Java代码实现，并分析了时间复杂度和空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

695.岛屿的最大面积

一、题目

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50

链接：695.岛屿的最大面积

二、分析

网格类的题目一般用DFS方法求解比较简单，下面一步一步构造出网格类题目的DFS代码。

首先，每个方格与其上下左右的四个方格相邻，则DFS每次分出四个岔

void dfs(int[][] grid, int r, intc){//r = row c= cloumn
	
	//dfs递归
	dfs(grid, r-1,c);//上边相邻网格
	dfs(grid, r+1,c);//下边相邻网格
	dfs(grid, r, c-1);//左边相邻网格
	dfs(grid, r, c+1);//右边相邻网格
}

接着，考虑网格边缘，对于网格边缘的方格，上下左右并不一定都有邻居，所以需要判断方格的位置，我们采用"先污染在治理"的方法，即先做递归调用，然后在DFS函数的开头判断。同时，还需要判断方格是否有岛屿(值是否为1)。

void dfs(int[][] grid, int r, intc){//r = row c= cloumn
	//判断网格边缘异常情况
	if(r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) return;
	//判断是否是岛屿    可以和上一步合并
	if(grid[r][c] != 1) reutrn;
	
	//开启DFS递归
	dfs(grid, r-1,c);//上边相邻网格
	dfs(grid, r+1,c);//下边相邻网格
	dfs(grid, r, c-1);//左边相邻网格
	dfs(grid, r, c+1);//右边相邻网格
}

但是这样还有一个问题:DFS可能会走回头路，会不停的兜圈子。如图
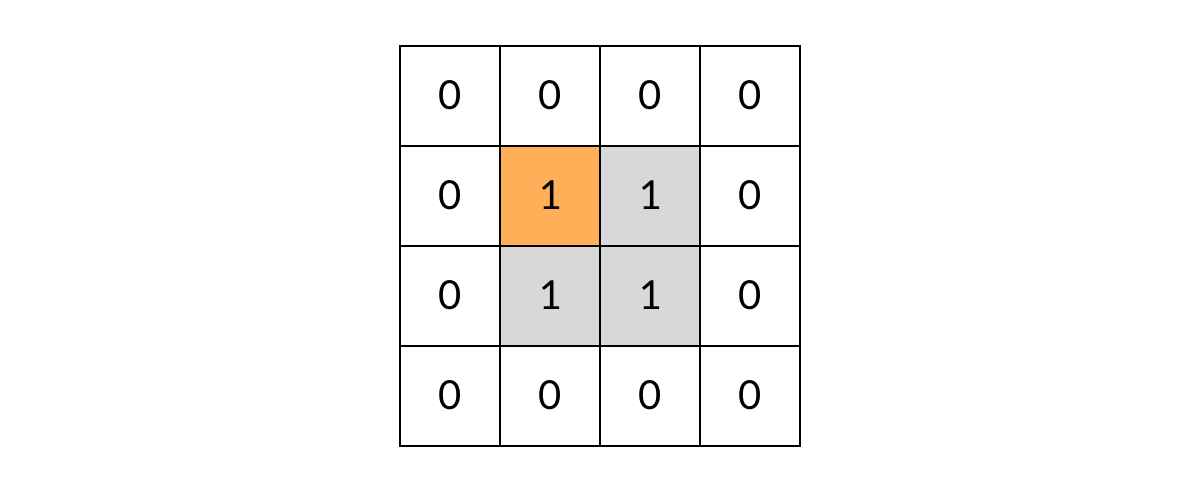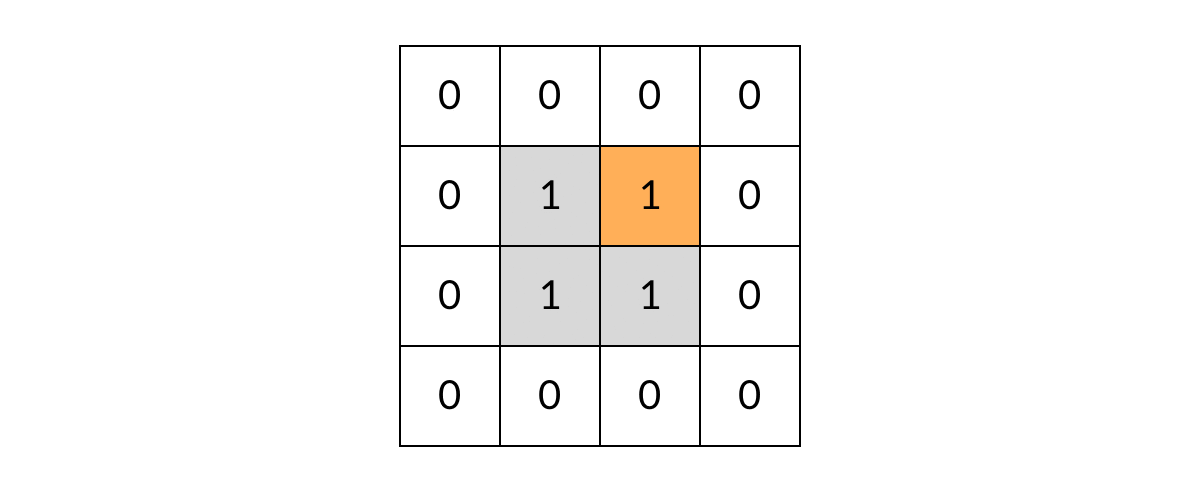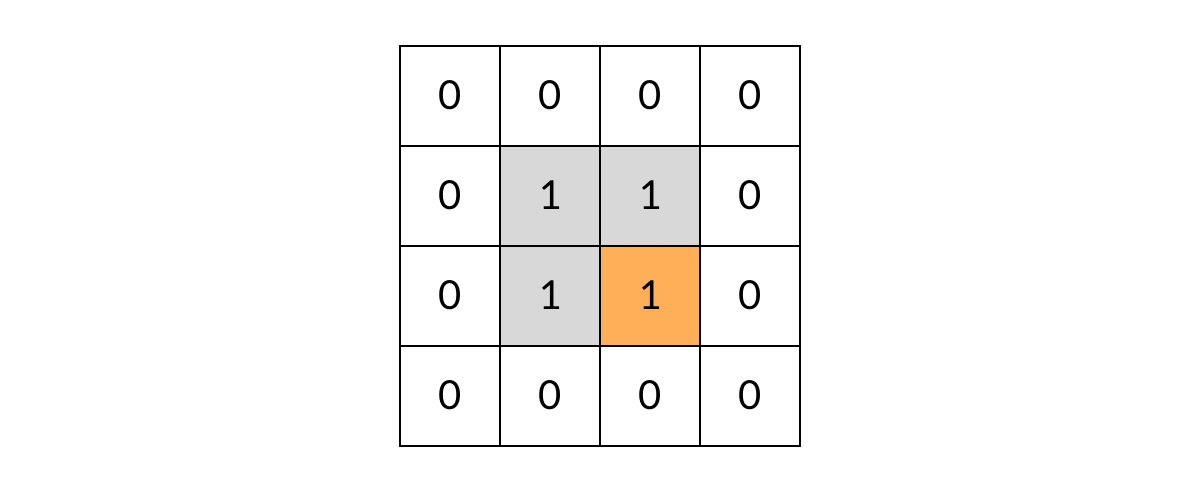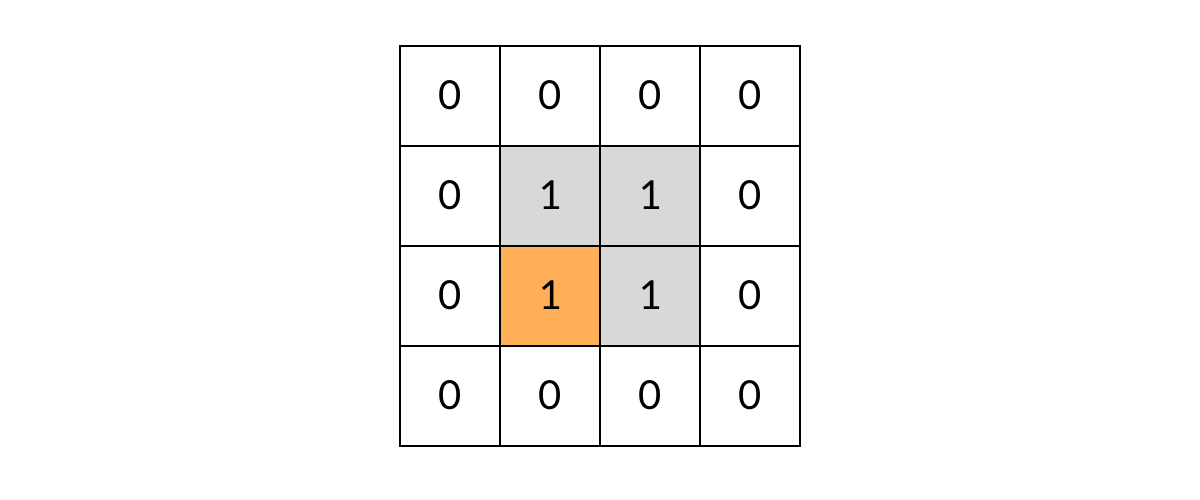
在这里插入图片描述

这样就需要我们标记走过的方格，保证方格不进行重复遍历。标记遍历过得方格，不需要使用额外的空间，只需改变方格中的值。我们可以用2表示已经遍历过的网格(也可以标记为0，把岛屿变成水，沉岛思想)。代码如下：

void dfs(int[][] grid, int r, intc){//r = row c= cloumn
		//判断网格边缘异常情况
		if(r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) return;
		
		//遍历过的网格会直接返回，不会产生重复遍历
		if(grid[r][c] != 1) return;
		
		//标记遍历过的网格
		grid[r][c] = 2;
		
		//开启DFS递归
		dfs(grid, r-1,c);//上边相邻网格
		dfs(grid, r+1,c);//下边相邻网格
		dfs(grid, r, c-1);//左边相邻网格
		dfs(grid, r, c+1);//右边相邻网格
	}

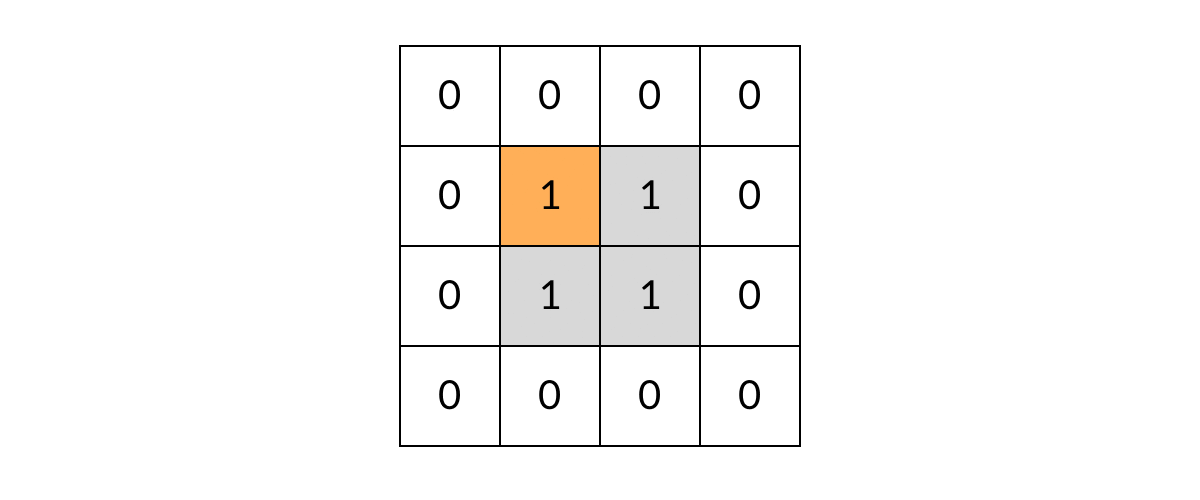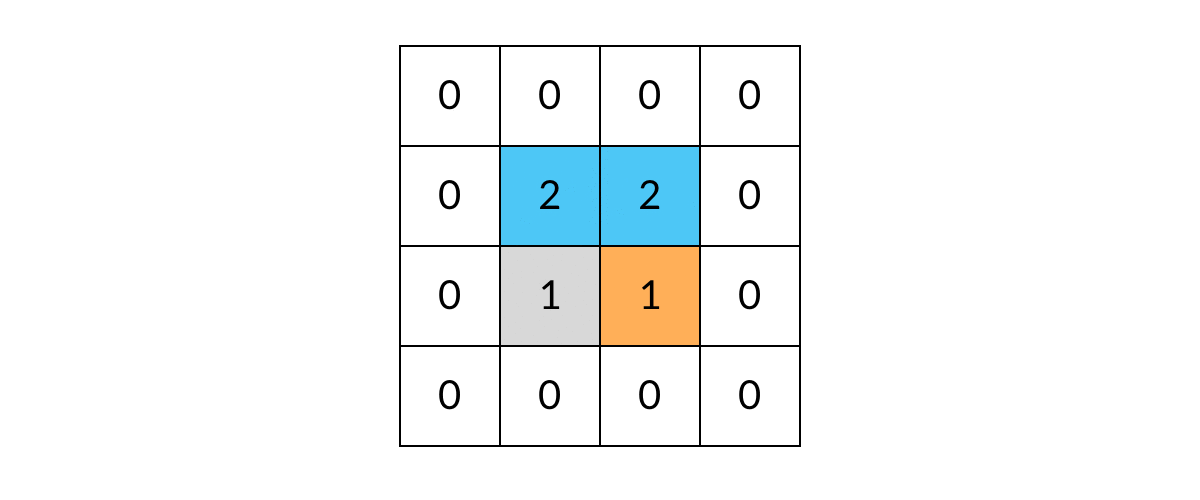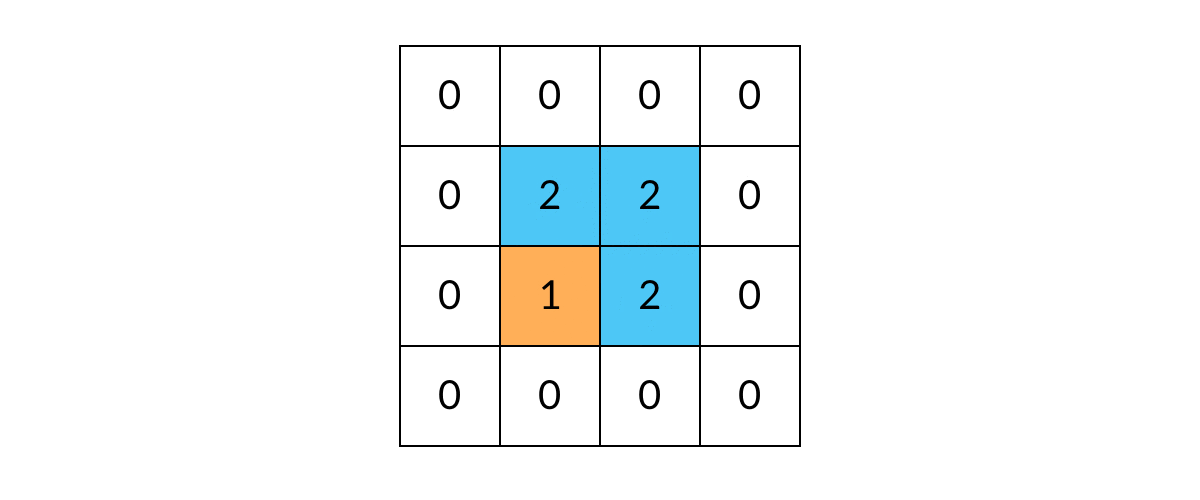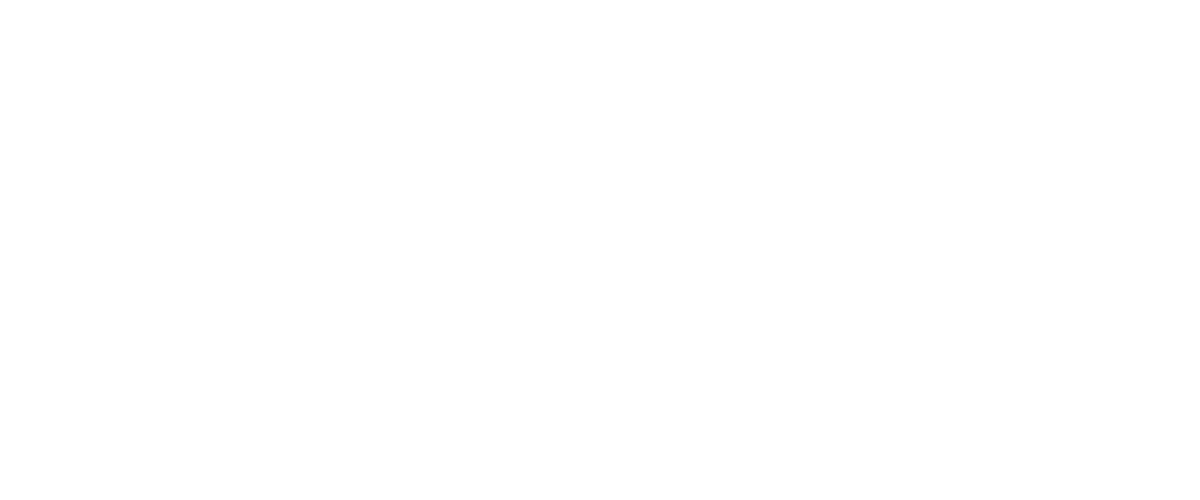
在这里插入图片描述

至此，问题的关键点已经解决，完整代码如下：

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
		if(grid == null || grid.length ==0) return 0;
		int res = 0;
		for(int r = 0; r< grid.length; r++){
			for(int c = 0; c<grid[r].length; c++){
				if(grid[r][c] == 1){ //是岛屿才开启递归
					int a = dfs(grid,r,c);
					res = Math.max(res,a);
				}
			}
		}
		return res;
	}
	int dfs(int[][] grid, int r, int c){//r = row c= cloumn
		//判断网格边缘异常情况
		if(r < 0 || r >= grid.length || c < 0 || c >= grid[0].length) return 0;
		
		//遍历过的网格会直接返回，不会产生重复遍历
		if(grid[r][c] != 1) return 0;
		
		//标记遍历过的网格
		grid[r][c] = 2;
		
		//开启DFS递归
		return 1 +
			+ dfs(grid, r-1,c)  //上边相邻网格
			+ dfs(grid, r+1,c)  //下边相邻网格
			+ dfs(grid, r, c-1) //左边相邻网格
			+ dfs(grid, r, c+1); //右边相邻网格
	}
}

上面已经是标准答案，可以稍微精简一下代码。

public int maxAreaOfIsland(int[][] grid) {
	if(grid == null || grid.length ==0) return 0;
		int res = 0;
		for(int r = 0; r< grid.length; r++){
			for(int c = 0; c<grid[r].length; c++){
				if(grid[r][c] == 1){ //是岛屿才开启递归
					res = Math.max(res,dfs(grid,r,c));
				}
			}
		}
		return res;
}
int dfs(int[][] grid, int r, int c){//r = row c= cloumn
	//判断网格边缘异常情况 + 判断是否是岛屿(遍历过的网格会直接返回，不会产生重复遍历)
	if(r < 0 || r >= grid.length || c < 0 || c >= grid[0].length || grid[r][c] != 1) return 0;
	
	//标记遍历过的网格  直接标记为0 沉岛思想
	grid[r][c] = 0;
	
	//开启DFS递归
	return 1 +
		+ dfs(grid, r-1,c)  //上边相邻网格
		+ dfs(grid, r+1,c)  //下边相邻网格
		+ dfs(grid, r, c-1) //左边相邻网格
		+ dfs(grid, r, c+1); //右边相邻网格
}

题解参考nettee的题解：网格类 DFS 的写法（C++/Java）

三、题解

精简java题解

public int maxAreaOfIsland(int[][] grid) {
	if(grid == null || grid.length ==0) return 0;
		int res = 0;
		for(int r = 0; r< grid.length; r++){
			for(int c = 0; c<grid[r].length; c++){
				if(grid[r][c] == 1){ //是岛屿才开启递归
					res = Math.max(res,dfs(grid,r,c));
				}
			}
		}
		return res;
}
int dfs(int[][] grid, int r, int c){//r = row c= cloumn
	//判断网格边缘异常情况 + 判断是否是岛屿(遍历过的网格会直接返回，不会产生重复遍历)
	if(r < 0 || r >= grid.length || c < 0 || c >= grid[0].length || grid[r][c] != 1) return 0;
	
	//标记遍历过的网格  直接标记为0 沉岛思想
	grid[r][c] = 0;
	
	//开启DFS递归
	return 1 +
		+ dfs(grid, r-1,c)  //上边相邻网格
		+ dfs(grid, r+1,c)  //下边相邻网格
		+ dfs(grid, r, c-1) //左边相邻网格
		+ dfs(grid, r, c+1); //右边相邻网格
}