人工智能基础_机器学习016_BGD批量梯度下降求解多元一次方程_使用SGD随机梯度下降计算一元一次方程---人工智能工作笔记0056

然后上面我们用BGD计算了一元一次方程,那么现在我们使用BGD来进行计算多元一次方程

对多元一次方程进行批量梯度下降.

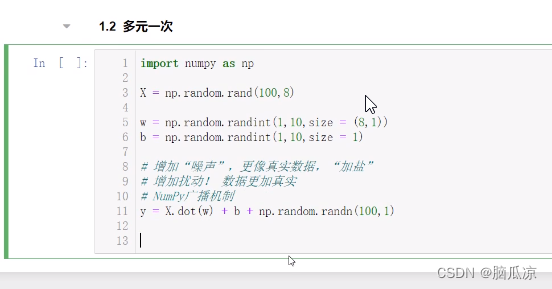
import numpy as np

X = np.random.rand(100,8)  首先因为是8元一次方程,我们要生成100行8列的X的数据对应x1到x8

w = np.random.randint(1,10,size = (8,1)) 然后我们生成8行1列的数据,从1到10之间,用来做为w1到w8 和X进行相乘,注意100行8列  和8列1行可以进行相乘,这个要明白

b = np.random.randint(1,10,size = 1) 然后我们生成,从1到10中生成1个,数来作为截距b
#增加“噪声”，更像真实数据，“加盐”

#增加扰动！数据更加真实

# Numpy广播机制

y=X.dot(w)+b+np.random.randn(100,1)

然后这个公式不用变,只是添加 一个噪声就可以了,添加一个,100行1列的数据,因为 我们这个:是矩阵运算,所以因为有100行x,所以就要有100行的随机噪声,然后要有一列,np.random.randn(100,1)函数生成的是服从标准正态分布的随机数，也称为高斯分布。这些随机数的均值为0，标准差为1。因此，你可以使用这个函数来生成一个100行1列的符合标准正态分布的随机数矩