超级会员免费看
本文介绍了无约束最优化问题和梯度下降的概念，详细讲解了梯度下降法寻找函数最小值的过程。通过求导数确定斜率，即梯度，逐步逼近最优解。讨论了学习率的影响，过大可能导致错过最优解，过小则收敛速度慢。最后，通过一个实例展示了如何用Python计算并可视化梯度下降找寻函数最小值的步骤。
然后我们来看一下梯度下降,这里先看一个叫
无约束最优化问题,,值得是从一个问题的所有可能的备选方案中选最优的方案,
我们的知道,我们的正态分布这里,正规的一个正态分布,还有我们的正规方程,他的这个x,是正规的,比如上面画的这个曲线,他的这个x,就是大于0的对吧,而现实生活中,
我们x的值可能是各种各样的没有约束的,基于没有约束的,这个问题..
我们来求导数,对y求导数得到,曲线的斜率,就叫做梯度下降
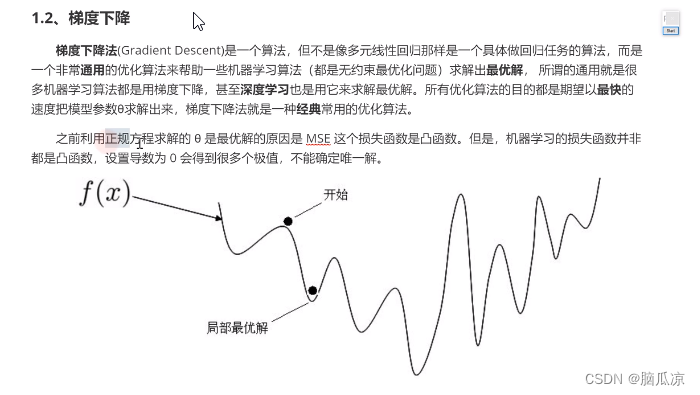
继续看,我们要找导数为0的,那么可以看到,底部
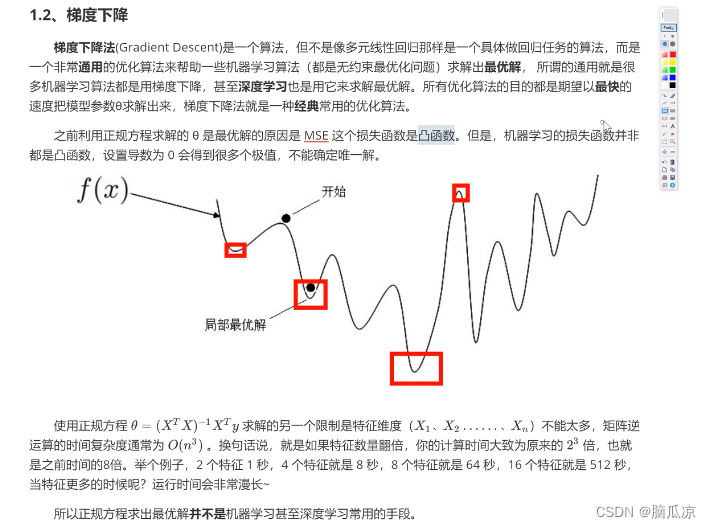
可以看到底部,和曲线的顶部都是斜率为0,导数为0对吧,但是
好在我们已经验证了,我们的最小二乘法,正态分布,对应的 是一个 开口向上的函数
所以我们找到的肯定是最低点对吧.
订阅专栏 解锁全文
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
