人工智能基础_机器学习002_正规方程_使用线性代数计算二元/三元/八元一次方程的绝对解_使用正规方程计算二元/三元/八元的绝对解_一切线性回归问题都可以这样解决---人工智能工作笔记0041

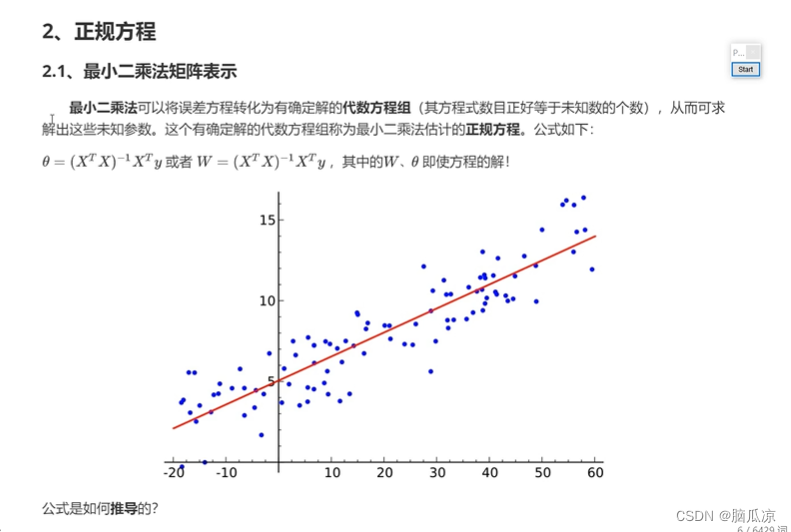
然后我们再来看最小二乘法,可以将loss函数,转换为有确定解的,代数方程组,其方程式数目,正好等于未知数的个数,从而可求解出这些未知参数. 也就是要求w和b对吧

这个

然后我们再来看,可以看到上面这个损失函数

其实就是这里的(hseta(xi)-yi) 其实就是,这里的yi是真实值,然后hseta(xi)是预测值,对吧,这里的hseata,就是我们说的w权重对吧, 然后这里xi,yi都表示某一个数据,

(hseta(xi)-yi) 然后又有一个平方,然后,还做了加和对吧,所有的(hseta(x1)-y1).....(hseta(xi)-yi) 的平方,加起来,然后/2 这里的/2我们先不管,这个是常数

然后之所以是最小二乘法,这里的平方可以看到吗? 平方就是这里的2,然后最小,就是保持结果最小,其实就是损失最小

我们要知道的是yi是真实值,hseata(xi) 这个hseata(xi),表示的是模型,算法,线性回归,方程对吧,

这个hseata(xi) 既然表示预测值,其实就是对应了,上一节我们的: