批量梯度下降_推导线性回归损失函数_以及利用代码实现批量梯度下降---人工智能工作笔记0027

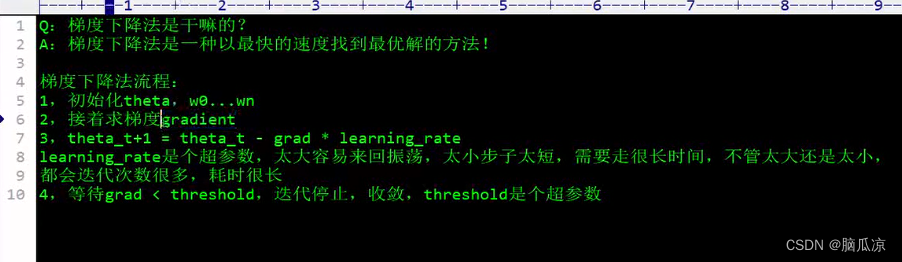
然后我们来看一下,怎么来求线性回归函数,那个目标函数,也就是损失函数的导数 

 

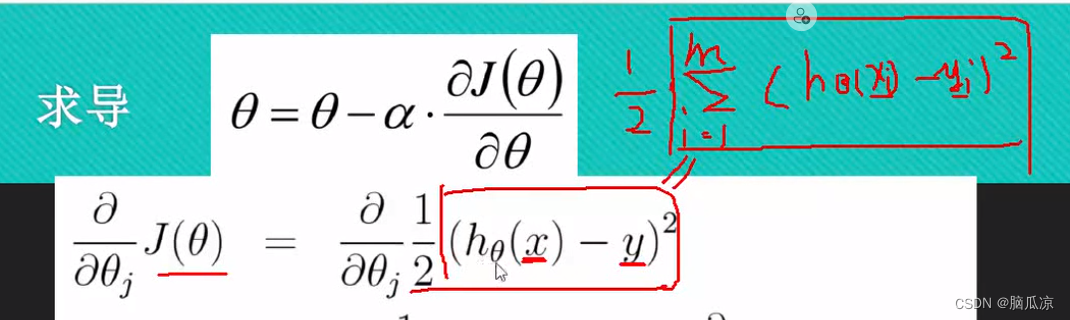
可以看到之前我们说的那个损失函数,也就是目标函数的公式是右上角的那个

现在转换成了下面的部分: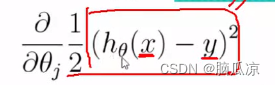

实际上这个表达方式很右上角的表达方式是一样的,右上角,这里的xi,表示是一个数,而

下面这个x y表示是一组数对吧.这里htheta (x) ,x这里是个矩阵,那么htheta 也是个矩阵,矩阵相乘,得到一个列向量,那么y也是一个列向量,列向量相减是线性代数的表达方式,而右上角是直接代数的表达方式,所以这两个是等价的.

下面是AI回答的:什么是线性代数,什么是直接代数,直接代数解决的问题更加的简单一些,

线性代数,升级到矩阵,向量等.

线性代数和直接代数的区别是一个比较复杂的问题，我尝试用简单的语言来解释一下。

线性代数是研究向量、矩阵、线性方程组、向量空间、线性变换等概念的数学分支1。它主要关注的是变量之间以固定比例变化的关系2，也就是说，如果一个变量增加或减少了一定的量，另一个变量也会按照一定的比例增加或减少。线性代数可以用来描述很多现实中的问题，比如图像处理、数据压缩、密码学等。

直接代数（Direct algebra）是我不太熟悉的一个术语，根据网上的资料3，它似乎是指用直接方法（Direct method）来求解线性方程组或微分方程的一种技巧。直接方法就是把原来复杂的问题转化为简单的问题来求解，比如把微分方程转化为线性代数问题3。直接方法有很多种，比如高斯消元法、克拉默法等。

所以说，线性代数和直接代数并不是同一层次上的概念，而是有所交叉和联系。你可以把直接代数看作是线性代数中的一个应用领域。

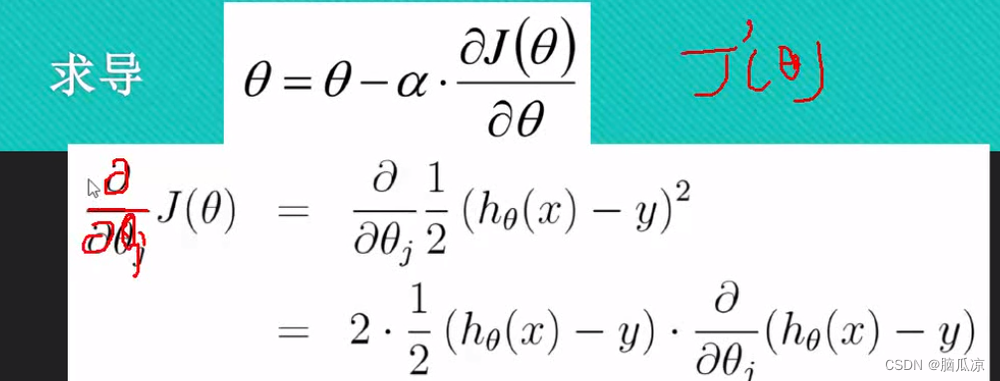
 这里的j(theta) 这里我们写一个撇,表示求导,这个我们知道,然后左侧的公式,为什么要写成那种符号呢,是因为

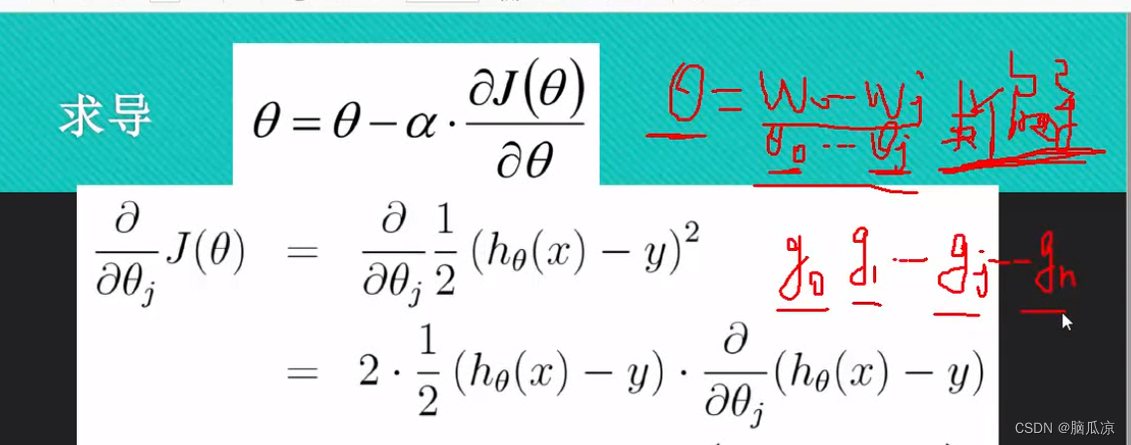
 可以看到是因为这里,theta是一组数值了对吧,这里是theta是一组的数值了,所以这里要求导数,就不能对某个theta求导数了,而是对所有的theta都要求导数,对所有的theta都求导数的话,这里叫做

求偏导,这里的theta其实就是对应的y=ax+b 这里的b是w0 a是w1,当然参数多的时候,还有w2,w3...wn对吧,所以这里的theta就是我们说的w,权重对吧.因为参数多,所以这里就是要求偏导了,对每个theta都要求导数.然后这个时候再做梯度下降的时候,就需要做批量的梯度下降了,因为

求出的导数,有多个,也就是斜率有多个,也就是对应的g有多个对吧.对应g0...gn对吧.

 如果我们的w权重比较多,参数比较多,那么我们的图,可以看到就不能这么画了对吧,这仅仅是针对一个参数一个theta画的.也就是只是考虑了一个维度的. 

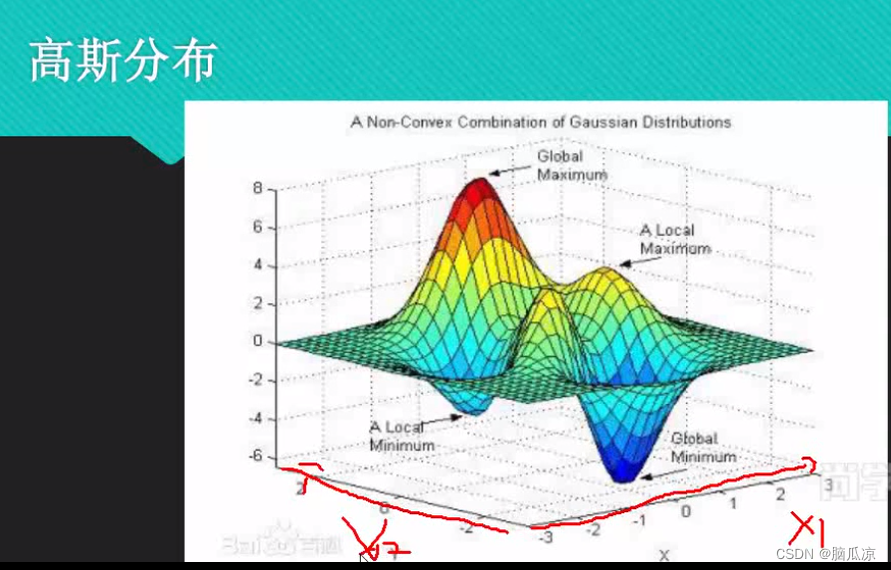
而如果参数比较多的话,也就是把上面那个1维的图给叠加起来画图,也就是上面这个样子的

可以看到上面画出了具有两个参数x1,x2的图

实际上上面的那个公式,就是表示了有多个theta的情况,要求导数的时候,也是求出多个导数,可以看到上面就是说,可以同时对多个参数,多个theta求导,得到多个g,斜率对吧.

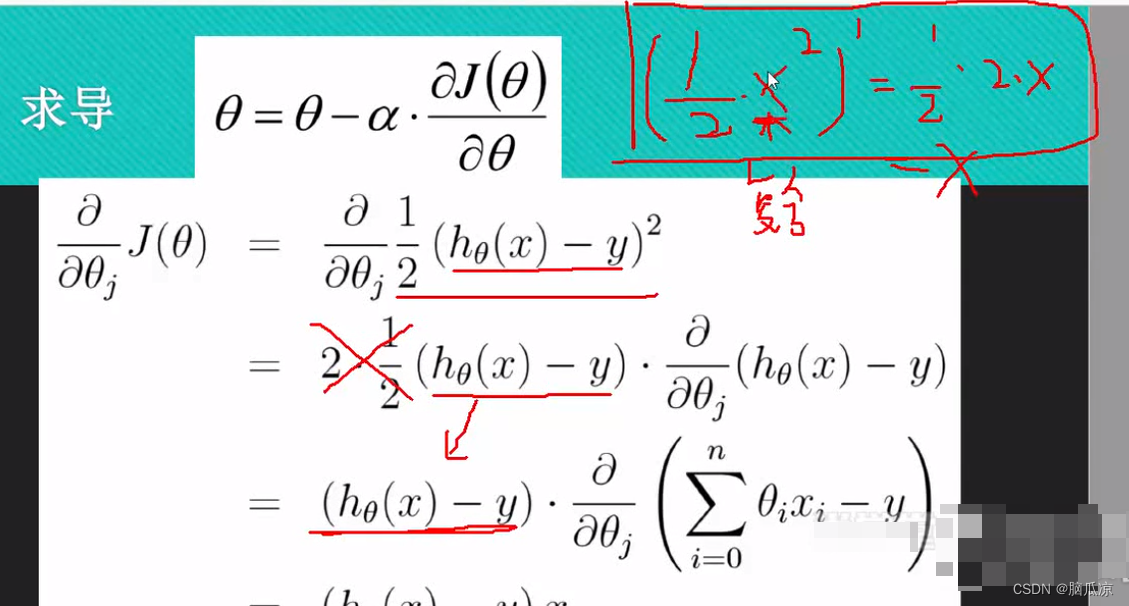
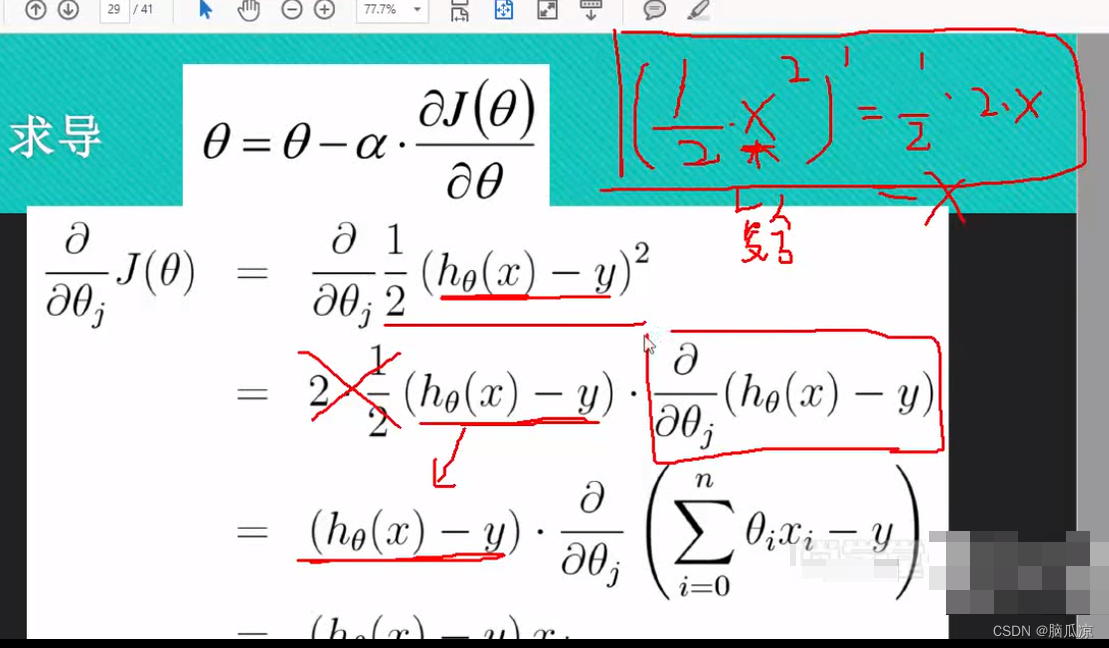
然后我们来看这里,我们开始对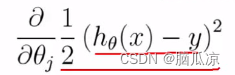这个公式进行求导

首先我们看这个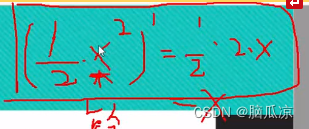这个求导的话,可以看到2分之一

的x^2 求导以后是 2分之一 . 2 .x,所以同理,

 

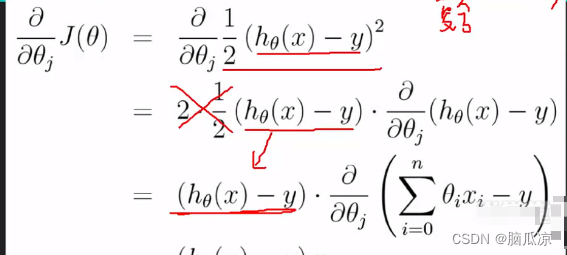
这个1/2 (hthetax - y)^2 就可以拆开,变成下面的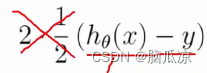对吧,

然后约掉就可以进一步变成这样了,然后为什么右边还需要

. 上一个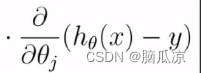这个部分,因为这里面的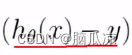

 这个部分,我们说hthetax是个矩阵,而对应的y也是个列变量,所以,也就是这里1/2(x)^2 对这个求导,

而这里面的x,是个复合函数,所以这里又需要对复合函数,hthetax-y 进行进一步的求导,

也就是对这个部分求导: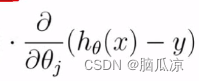

 

然后我们再来看一下如何对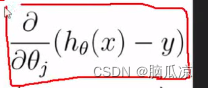这个部分来求偏导数

因这个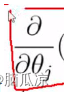这个部分其实表示的是,里面的hthetax是个矩阵,然后y是个列变量

 这个要明确

 

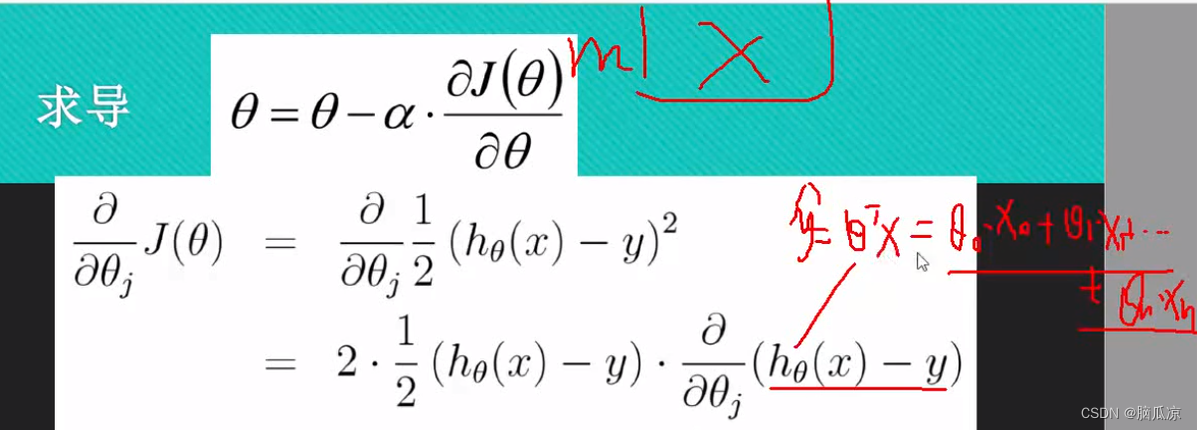
然后我们再来看一下,这里的x要知道是一个m行n列的矩阵,然后再来看这里的

这个hthetax,其实我们可以写成,yhat = theta T x对吧,然后这个

theta T x 可以写成theta0.x0+theta1.x1...+thetaj.xj+....thetan.xn 对吧,可以把这个写开了

 

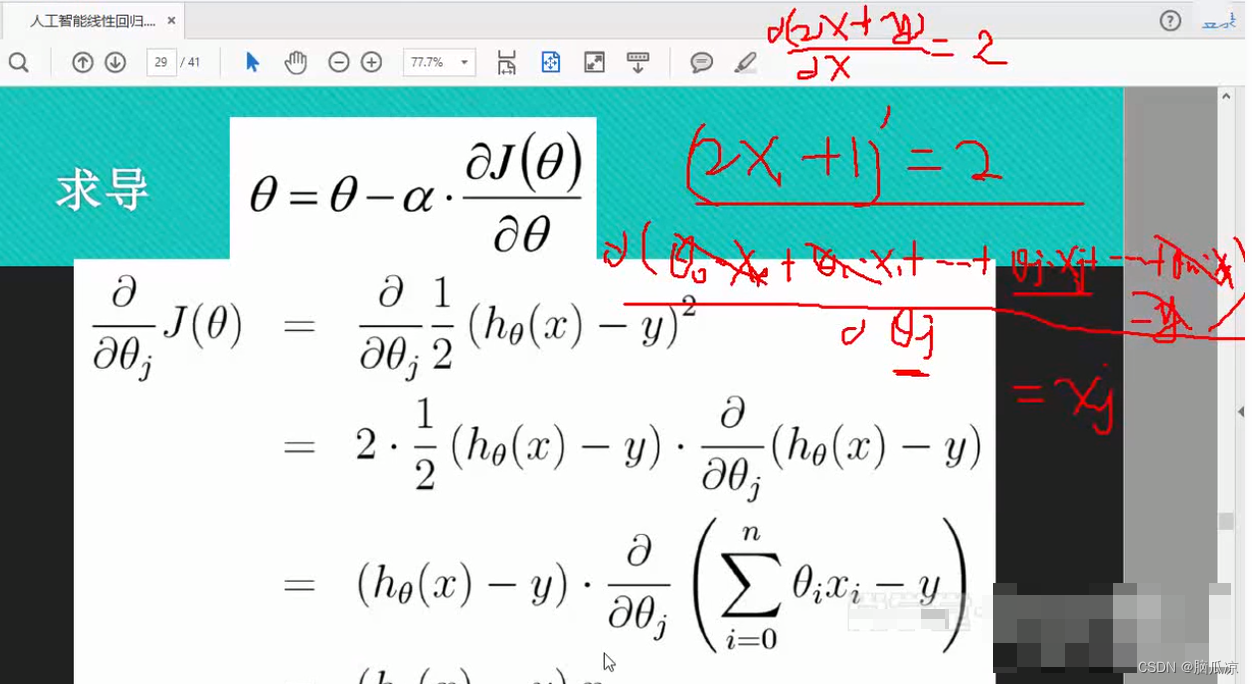
然后写开了以后怎么求偏导呢,可以看到,我们先看这个2x+1 的导数 =2 对吧,所以根据这个原理,

我们这个hthetax -y 可以写成 theta0.x0+theta1.x1...+thetaj.xj+....thetan.xn -y对吧,而这里的

跟2x+1 一样,这里对这个求导,就可以看成是 -y 这里就把y忽略就可以了,然后

如果我们把theta看成x的话,因为在之前的,那个正态分布图中,我们就把theta当成是x轴了对吧

求theta点对应的斜率,这里也一样,我们把theta看成x坐标,那么,这个  hthetax -y 可以写成 theta0.x0+theta1.x1...+thetaj.xj+....thetan.xn -y  的导数就是xj对吧

 

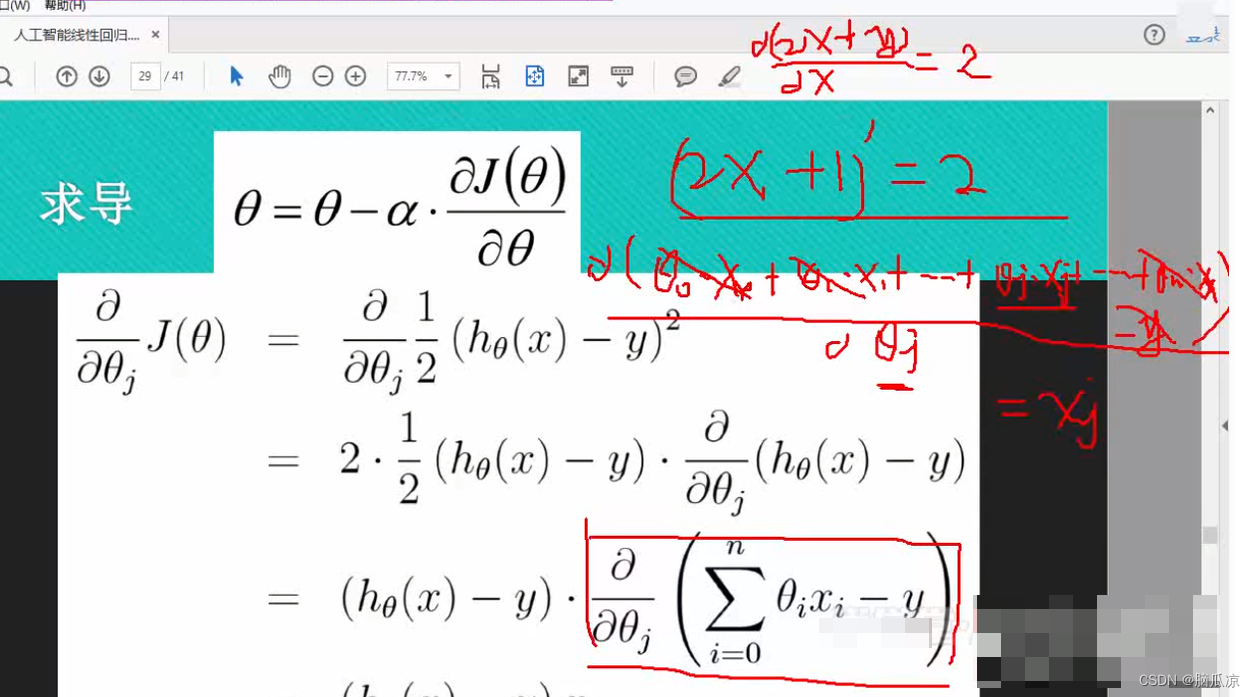
可以看到所以这里,为什么是xj呢?这里xj表示一个代表对吧, 因为我们看到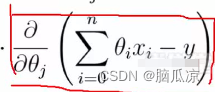这里是用的thetaj对吧,我们说把theta看成了x坐标了,所以这里,

我们那个公式的写法是:hthetax -y 可以写成 theta0.x0+theta1.x1...+thetaj.xj+....thetan.xn -y

如果按照我们之前看的那个正态分布图来看,我们把theta当成x坐标的值,那么对应的

上面的公式就可以写成:hthetax -y = theta0.x0+theta1.x1...+thetaj.xj+....thetan.xn -y

把这个写成:注意这里的X,我们就类似于2x+1 中的2对吧,我们改个名字叫X吧

(hthetax -y)j = x0.X0+...+xj.Xj+....xn.Xn -y 这里因为求的是j对应的导数所以这里的结果

就是Xj了 ,注意这里的x0...其实是theta对吧,然后所以对应的结果就是xj了,体会体会吧..

所可以看到,最后我们就得到了一个J(theta)这的导数了,就是包含,x矩阵和 y列变量的导数

也就是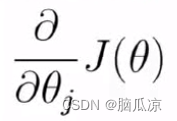 = (htheta(x) -y).xj 对吧

 

  j(theta)`= (htheta(x) -y).xj 对吧所以这个导数,如果我们输入一个xj,也就是对应时刻的x矩阵,然后再输入那一时刻的theta的所有值,也就是之前我们说的那个正态分布图中的对应的theta值,然后再把对应的y值带入进去,就可以得到那一个时刻的所有的theta的导数了对吧.

然后我们再来明确一下,这里的xj,表示的是某一列对吧,因为x是m行到n列的矩阵,然后

i从0到n,所以这里的j,其实就是x从0列到n列的某一列对吧.

 然后这里我们再来看一下,这里( htheta(x) - y ) xj 这里要知道是如何计算的,

我们知道这里,因为m*n是个矩阵要知道是m行n列的,所以这里的htheta是一个n*1列的列变量,好好考虑,不是太好理解, 其实也好理解,因为我们要知道x是一个m*n的矩阵,m行n列,所以,就需要一个,

1列n行 的数,来与它计算,因为x有n列,所以就要有n行,1列的theta才能进行计算,然后y是一个m行1列的值m*1列的值,也就是m行一列的数据, 所以这个结果,

也就是htheta(x)-y 这个得到也是一个m行一列的数据,然后再去乘以xj,注意,xj 其实是m行中的具体哪一行对吧,也是m行1列的数据,所以他们两个相乘,就需要有一个进行转置,最后得到的gj ,也就是这多个导数了对吧.

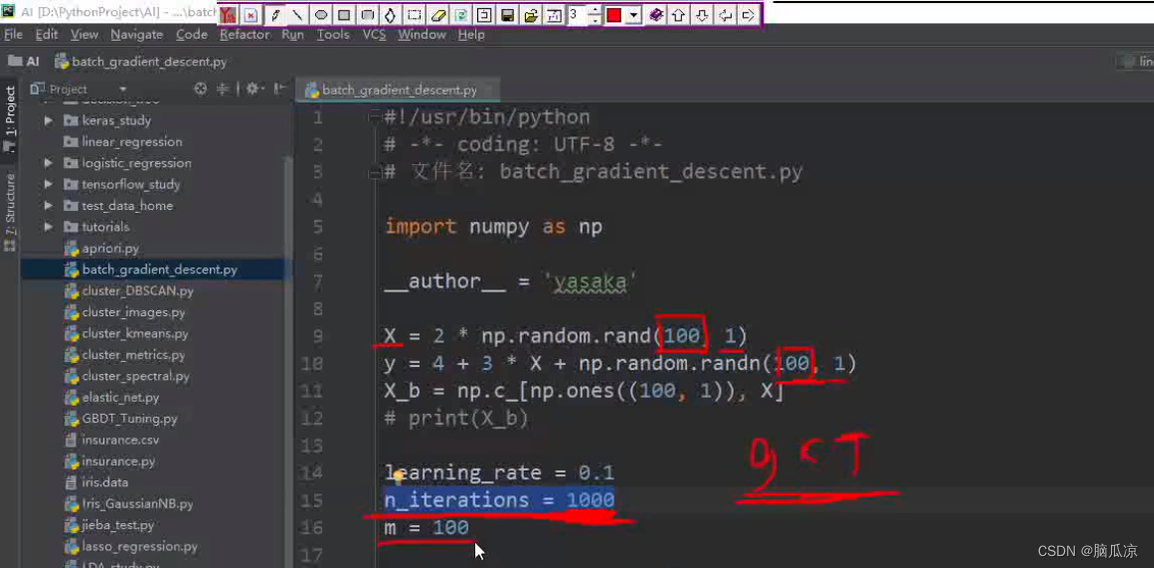
然后我们用代码来看一下这里,怎么样,使用代码实现一下

首先import numpy as np 导入 数学集合的的包对吧

然后X= 2 * np.random.rand(100,1) 定义一个 0 到1 的,100行,1列的数据对吧,这里是0到2 ,因为乘以2了对吧

然后定义Y = 4+ 3 * X + np.random.randn(100,1) 这里 是根据X的值得到一组Y的值,这个y是真实值.

然后,然后我们说y = ax+b 这里的b我们 可以认为想x0*b + x1*权重w1+x2*w2... 这里我们让x0 =1 ,

那么加的这个b 就是原值了,所以这里

x_b = np.c_[np.ones((100,1)),X] 将,一个100行1列的1 拼接到我们的X上面去.

这样我们的x数据,就是第一列全部都是1了.符合我们x0 =1的规则.

然后这个learning_rate = 0.1 是学习率,我们指定的,然后

n_iterations = 1000 是迭代次数,比如我们让他迭代1000就停止,在机器学习中,由于计算量过大,如果等着他结果收敛的话,那么可能会等很久,所以这里,我们就指定迭代1000,不管结果准不准,都

不继续进行了.

然后因为我们初始化X值的时候,是100行一列, y值也是100行一列,所以这里我们是100个样本,

m = 100

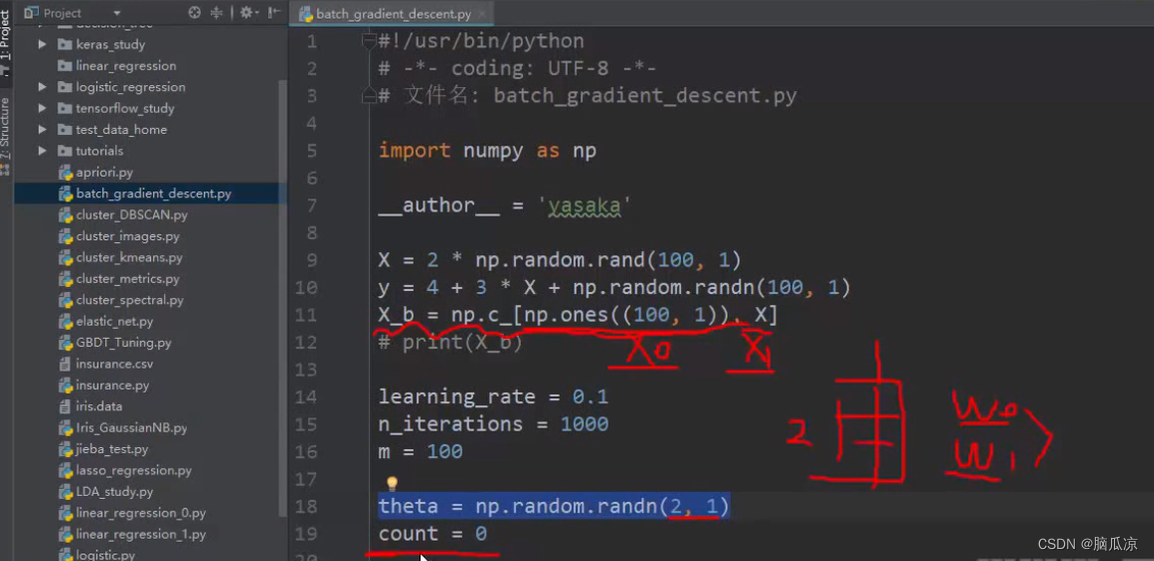
然后我们继续说,这里这个

theta = np.random.randn(2,1) 这里是获取一个2行 一列的数据 ,其实就是准备了,我们之前说的

正态分布中的,theta对吧,因为这里我们,x是两维度的,所以这里我们也就相当于有,两个

正态分布,然后,这里我们就要输入两个theta了,两个权重对吧,可以看到

然后这里的count = 0 这里我们先不用管

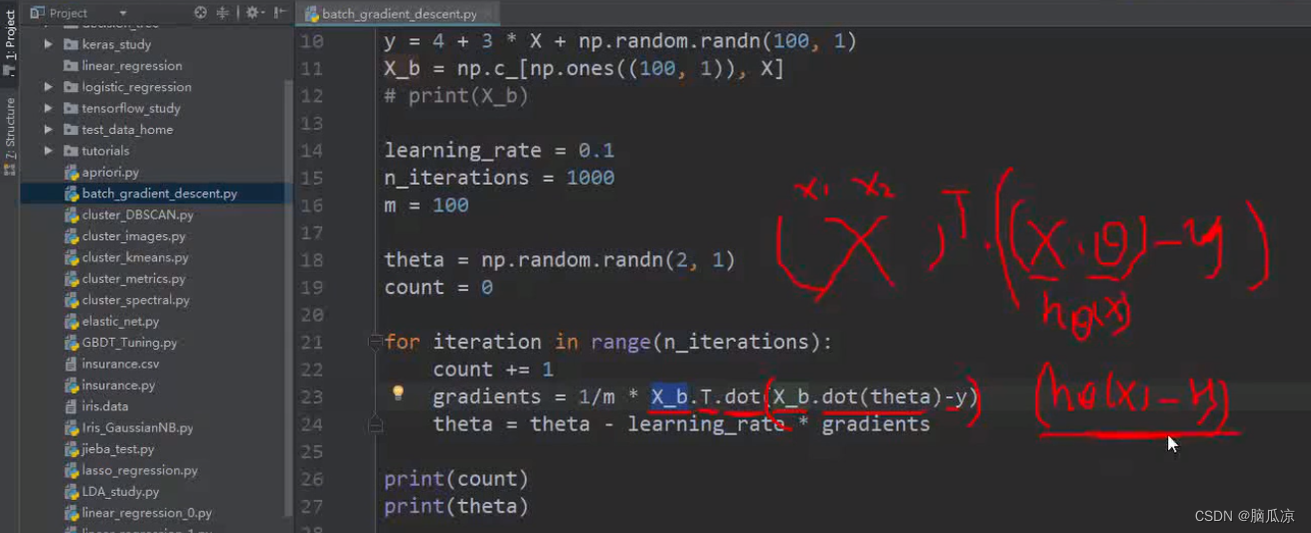
然后我们再来看继续

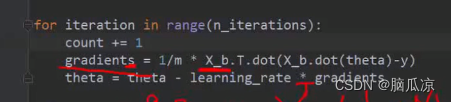
这里for interation in range(n_iterations);

其实就是循环n_iterations,这个n_iterations是1000对吧所以这里就是从0到999进行循环

对吧

然后我们再看

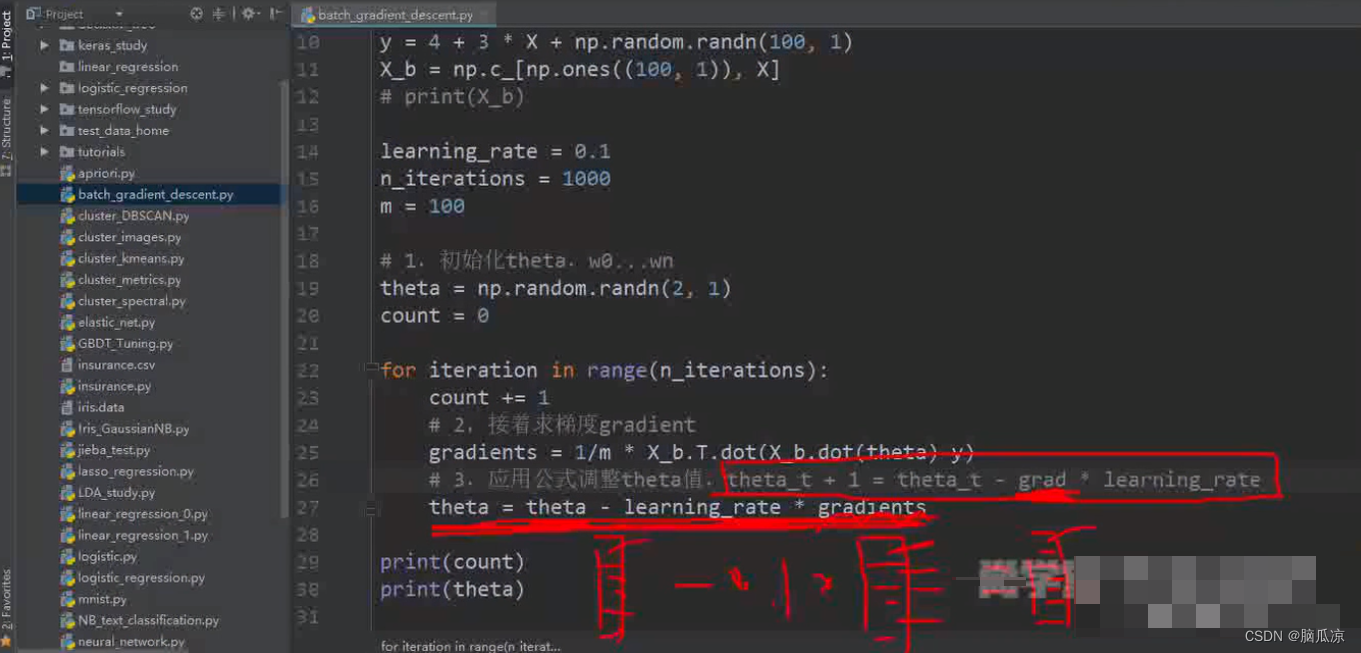
gradients = 1/m * x_b.T.dot(x_b.dot(theta)-y)

可以看到这个公式其实就是,对应的X_b,这个矩阵包含了两个参数的对吧x1,x2 ,然后 * x_b 再 * theta 然后-y 对吧就是右上那个公式对吧

然后这里的 x_b.dot(theta) - y 其实就是(htheta(x1)-y) 对吧,其实就是套的上面咱们说的那个公式

对吧.

 

 具体我们看,其实就是之前我们这个公式,我们说

(htheta(x) - y) * xj 这里的 htheta(x) - y 我们说是m行1列的矩阵,然后xj,我们说也是m行1列的矩阵

那么,两个m行1列的矩阵相乘,我们说矩阵相乘需要有一方需要转置对吧,所以这里我们就有一个转置对吧,这里我们转置的是xj对吧.

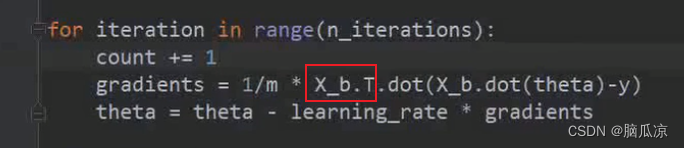
这里.这个就是我们说,两个矩阵相乘,需要将一方进行转置,这里我们转置的是xj,也就是

上面的x_b.T对吧

 

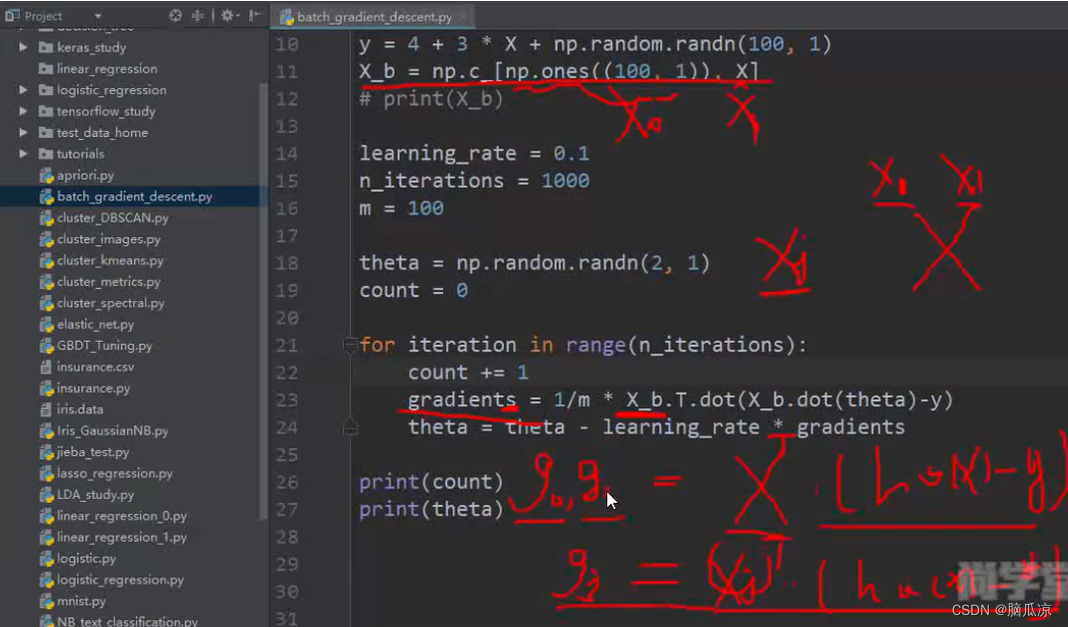
然后我们这里还需要知道,这里我们的xj,我们之前说是一列数据,也就是m行n列中的一列对吧,但是

要注意,我们这里的话,xj,因为是x_b对吧,而这个x_b,我们知道,其实是,有两列对吧,一列是100行,1列的随机出来的0到2的值,一列是,100行1列的1对吧,所以现在我们,这里的,x,实际上是100行2列的数据,然后对应的xj,也是100行2列的数据,然后,这个时候,我们做梯度下降.

也就是这个部分梯度下降,以后得到的值,可以看到是g0 g1 也是两个对吧,

因为我们知道,以前100行1列的数据,这个xj,我们讨论的是一维的...现在是两维的,所以

得到的斜率,也是2个

 下面具体我们再来说说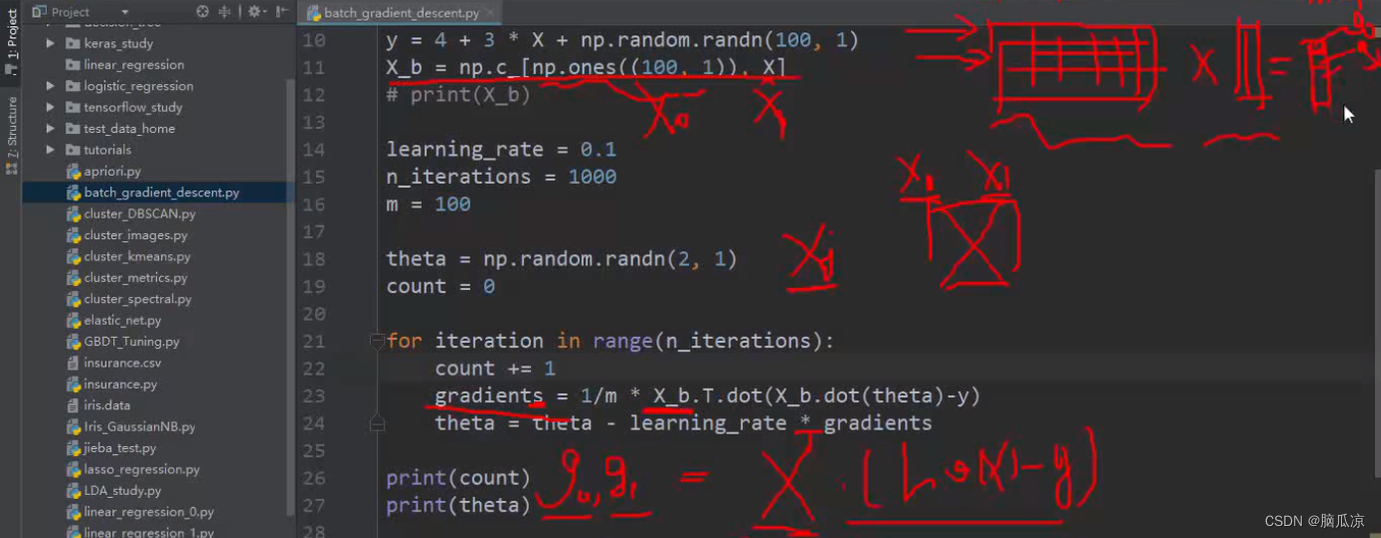

可以看到,我们说这里xj . (htheta(x) -  y) 实际上是 一个100行1列的值  *  100行1列的值对吧

看右上角,那么由于我们的转置,这里我们的xj,也就是x_b.T 对吧,本来是100两2列的值,现在

应该说是2行100列的值了,因为转置了,那么,2行100列的值  和 100行1列的值进行相乘

这里的这个两行100列,其实就是右边

也就是说左边是

左边是m*n 这里是100行2列对吧,中间那个n*1对吧,

这里为什么说是n*1呢? 因为这里我们的xj,我们写的也是x_b,只不过对x_b进行了,

x_b.T转置对吧,所以如果,x_b是100行2列,那么转置以后就变成了2行100列,是个列向量,而

一个矩阵*2行100列的列向量的话,会,左边矩阵* 列向量的第一行会得到一个值,然后

左边矩阵*列向量第二行又得到一个值,这里要知道这个规则,所以就是得到了

两个g了对吧,也就是g0,g1,也就得到了这两个,正态分布的,对应的我们输入了两个theta的

斜率了对吧.这个需要好好理解一下

 

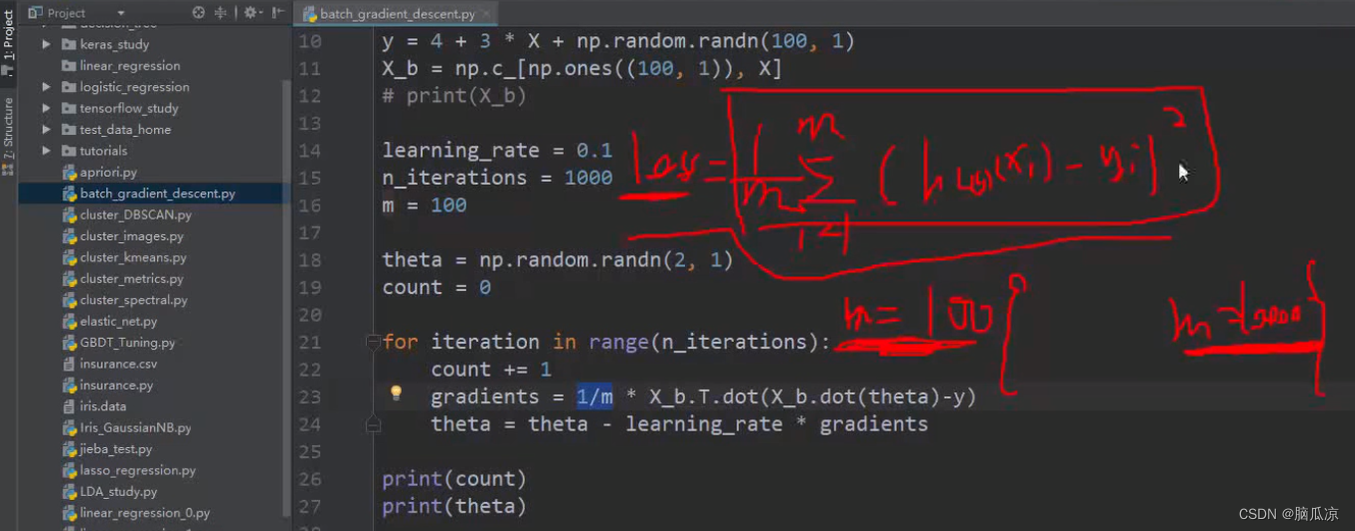
然后我们再看,这里损失函数我们已经计算出来了

readients = x_b.T.dot(x_b.dot(theta)-y)对吧为什么,前面要 * 1/m 呢?

注意,我们一般来说,现在是100个样本数据对吧,我们说如果样本数据越大,可以知道

loss,这个损失函数越大对吧,那么不对啊.

我们说,样本越大,做出的预测越准确啊...所以这里我们就在前面,写了一个1/m ,*了这个1/m

以后,我们会发现,随着m,样本数增大,我们的损失反而越来越小了对吧,这个就是* 1/m的原因

,也就是相当于这里我们求的是一个平均的损失.让平均损失越小,那么样本数量越大

 

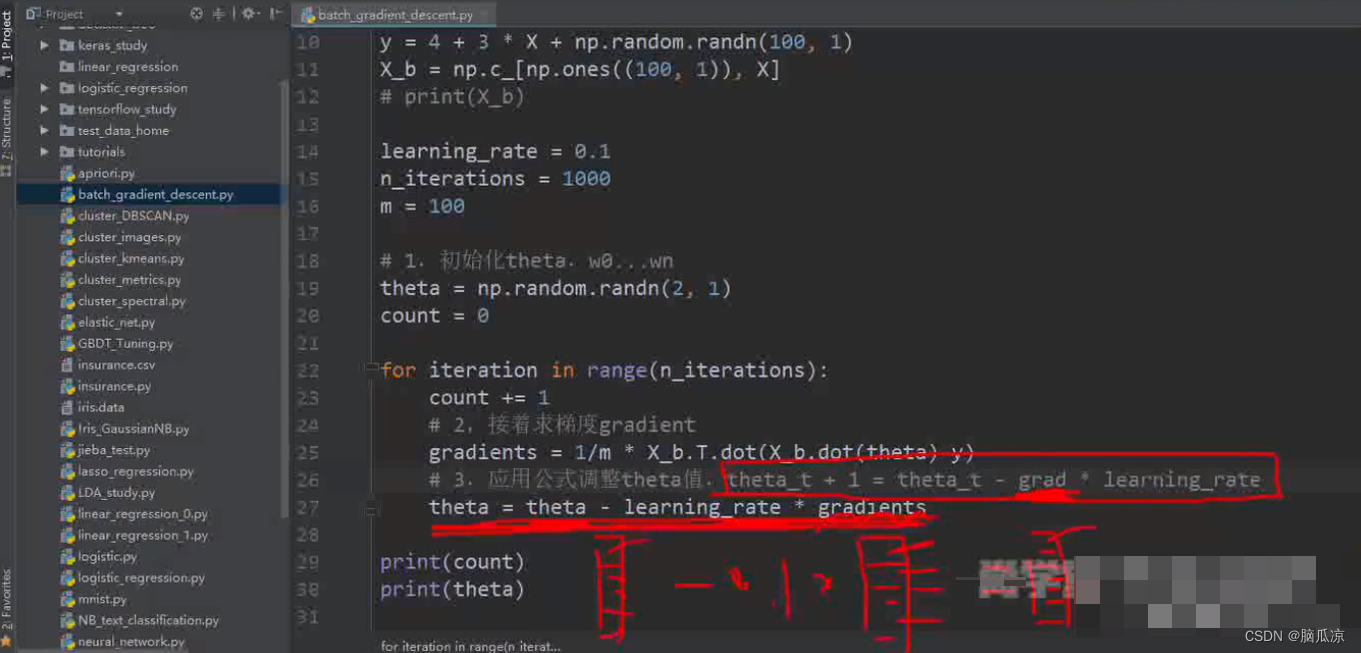
然后我们把批量梯度下降这个注释写上.

然后这里要知道,这里的梯度,我们之前说的,g,在我们这里面就变成了复数了,就有2个了对吧

因为,我们先看这里,我们的theta = np.random.randn(2,1) 是一个两行1列的,什么?

标准正态分布中的值对吧,因为我们,之前也说,theta是符合标准正态分布的,所以我们获取了随机的

一个正态分布中的值,来做为初始值.

然后紧接着,我们得到了g0,g1以后,带入:

theta_t+1 = theta_t - grad * learning_rate 对吧

这里,我们这个grad,这里限制是一个2行1列的列向量对吧,* learning_rate 常数以后,还是一个

列向量对吧,然后这个列向量,再跟原来的theta_t 做减法的话,得到的还是一个列向量,

这样就得到了第二个theta_t+1了,然后就可以继续做批量梯度下降了

 

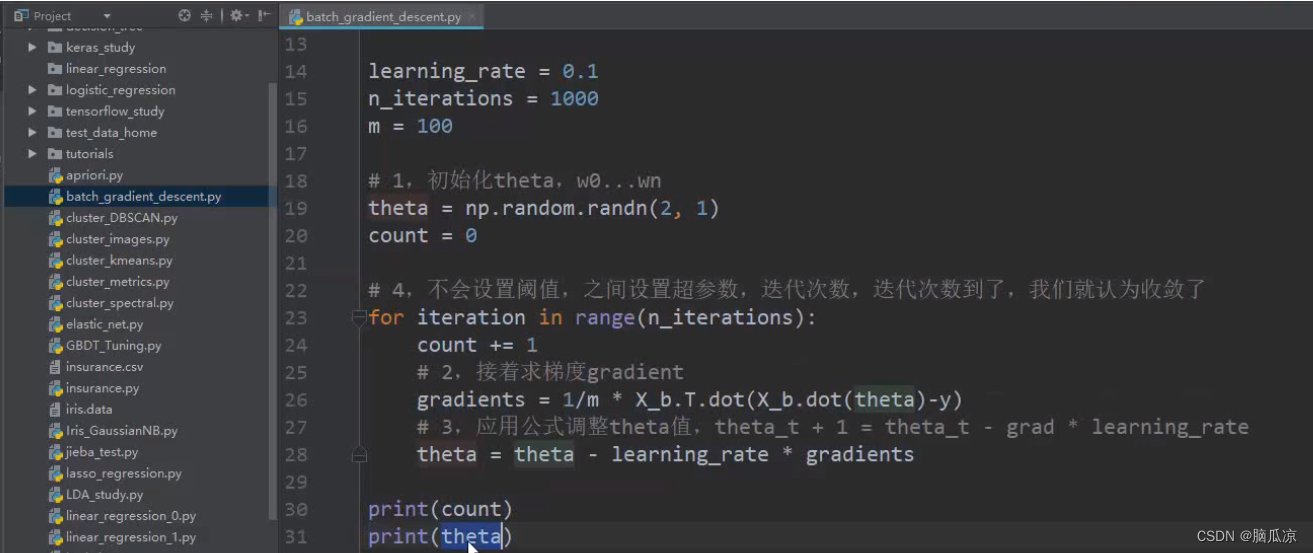
然后还要注意,实际上我们工作的时候,是不设置阈值的,我们说让他不停的迭代,直到,

结果收敛,也就是找到解析解对吧,但是实际上,要找到解析解,或者是说达到我们需要的阈值,有时候

需要的实际太久,所以我们一般往往,比如我指定,让他迭代1000次就停止,我们就认为已经收敛了.

即使是没有收敛也这么认为.

那么如果没有收敛怎么办?我们有其他的办法来防止它不收敛,后面会说到

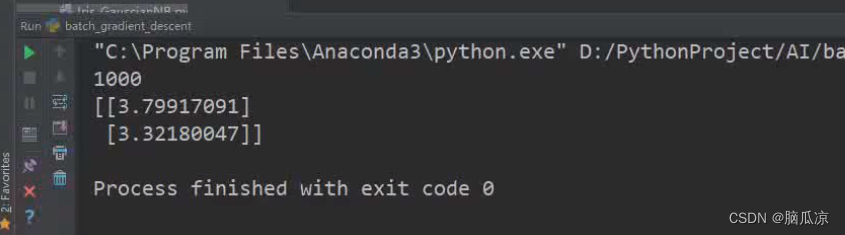
然后我们执行,这里执行1000次看看结果,可以看到,得到了

y=3x+4 这里的...参数可以看到b是3.7  a是3.3对吧... 

 

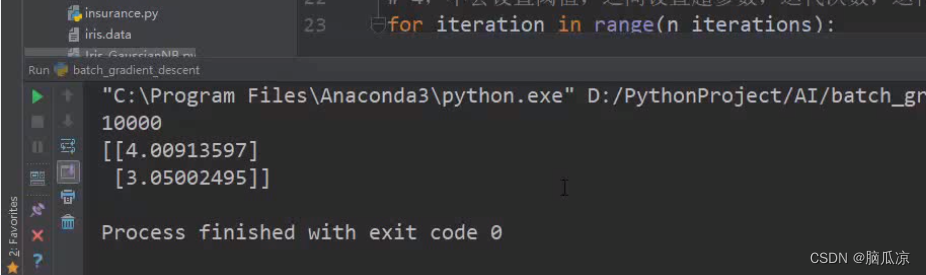
然后我们迭代10000次看看,结果就比较准确了对吧.

然后我们再来看看这个文件的名字,可以看到是batch开头的,也就是说,这个batch是批的意思,

也就是批量的进行梯度下降,因为我们的维度多对吧,如果后面做图像处理什么的,可能会用到

很多的参数,甚至100万个,那么这个时候,都是用这种批量梯度下降来求解问题的.

 

然后我们说随机梯度下降,我们说梯度下降,还叫做SGD对吧

这里s是什么意思呢?

 

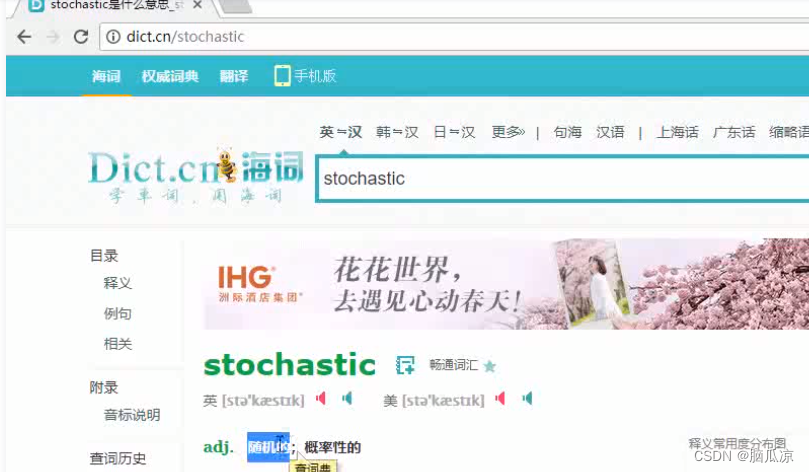
我们查一下可以看到是随机的意思对吧.

所以这里梯度下降也就说的是随机的对吧,随机的梯度下降,还给个随机的初始值对吧.

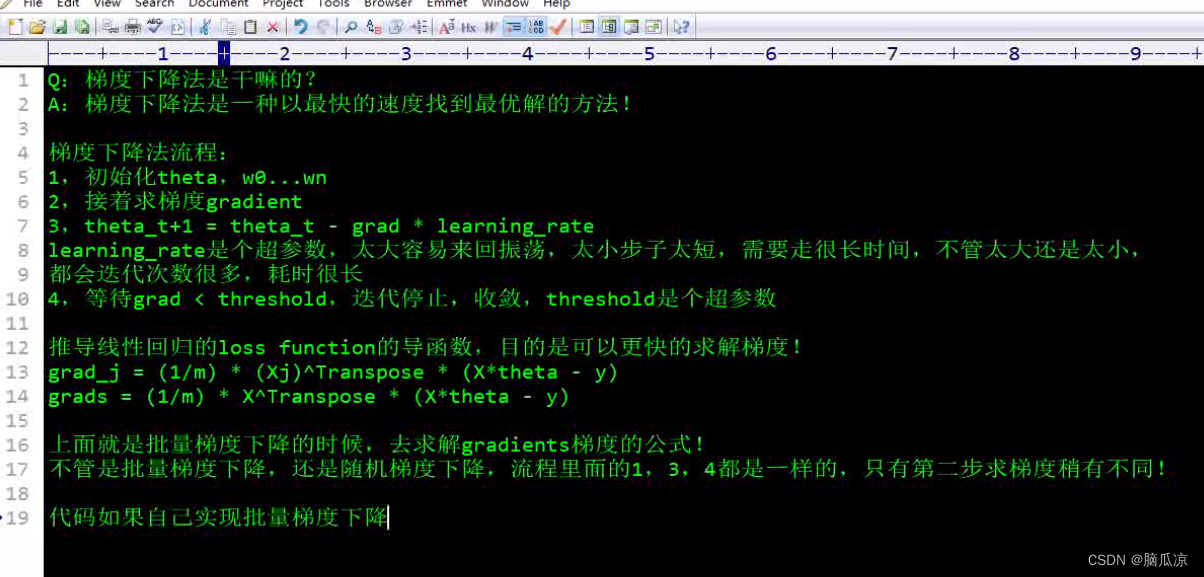
然后再去总结一下去看看