我的遗传算法实验

遗传算法实践

一、实验内容

通过python代码实现遗传算法，理解遗传算法相关概念和实现流程。

二、实验目标

• 了解遗传算法的思想
• 熟悉遗传算法实现的流程
• 掌握遗传算法的实现和可视化步骤

三、实验环境

• 操作系统：Ubuntu16
• 工具软件：jupyter notebook、Python 3.6.13
• 硬件环境：无特殊要求
• 核心库：
  • numpy
  • matplotlib

四、实验原理

1、遗传算法概念

我们先从查尔斯·达尔文的一句名言开始：

能够生存下来的往往不是最强大的物种，也不是最聪明的物种，而是最能适应环境的物种。

遗传算法的思想来源于达尔文的进化学说，是一种模拟‘适者生存’法则的优化算法。

让我们用一个基本例子来解释 ：

我们先假设一个情景，现在你是一国之王，为了让你的国家免于灾祸，你实施了一套法案：

• 你选出所有的好人，要求其通过生育来扩大国民数量。
• 这个过程持续进行了几代。
• 你将发现，你已经有了一整群的好人。

这个例子虽然不太可能，但是我用它是想帮助你理解概念。也就是说，我们改变了输入值（比如：人口），就可以获得更好的输出值（比如：更好的国家）。现在，我假定你已经对这个概念有了大致理解，认为遗传算法的含义应该和生物学有关系。

2、生物学启发

「细胞是所有生物的基石。」由此可知，在一个生物的任何一个细胞中，都有着相同的一套染色体。所谓染色体，就是指由 DNA 组成的聚合体。

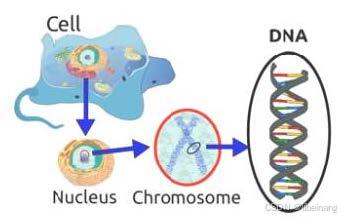
传统上看，这些染色体可以被由数字 0 和 1 组成的字符串表达出来。

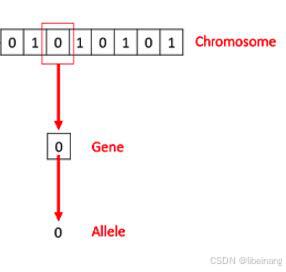
一条染色体由基因组成，这些基因其实就是组成 DNA 的基本结构，DNA 上的每个基因都编码了一个独特的性状，比如，头发或者眼睛的颜色。

3、遗传学算法定义

首先我们回到前面讨论的人口例子，并总结一下我们做过的事情。

1. 首先，我们设定好了国民的初始人群大小。
2. 然后，我们定义了一个函数，用它来区分好人和坏人。
3. 再次，我们选择出好人，并让他们繁殖自己的后代。
4. 最后，这些后代们从原来的国民中替代了部分坏人，并不断重复这一过程。

遗传算法实际上就是这样工作的，也就是说，它基本上尽力地在某种程度上模拟进化的过程。

因此，为了形式化定义一个遗传算法，我们可以将它看作一个优化方法，它可以尝试找出某些输入，凭借这些输入我们便可以得到最佳的输出值或者是结果。遗传算法的工作方式也源自于生物学，具体流程见下图：

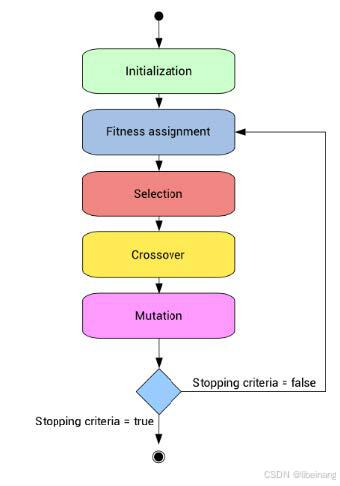
4、遗传学算法流程

• 初始化种群
• 计算适应度（适应度函数）
• 选择运算
• 交叉运算
• 变异运算
• 适应度运算
• 迭代至种群出现最优

5、背包问题解释遗传算法具体流程

为了让讲解更为简便，我们先来理解一下著名的组合优化问题「背包问题」。（是不是跟贪心算法有点相似😊）

比如，你准备要去野游 1 个月，但是你只能背一个限重 30 公斤的背包。现在你有不同的必需物品，它们每一个都有自己的「生存点数」（具体在下表中已给出）。因此，你的目标是在有限的背包重量下，最大化你的「生存点数」。

物品项	物品重量	对应生存点数
睡袋	15	15
绳子	3	7
皮刀	2	10
手电筒	5	5
瓶子	9	8
葡萄糖	20	17

5.1 初始化

这里我们用遗传算法来解决这个背包问题。第一步是定义我们的总体。总体中包含了个体，每个个体都有一套自己的染色体。
我们知道，染色体可表达为二进制数串，在这个问题中，1 代表接下来位置的基因存在，0 意味着丢失。（译者注：作者这里借用染色体、基因来解决前面的背包问题，所以特定位置上的基因代表了上方背包问题表格中的物品，比如第一个位置上是 Sleeping Bag，那么此时反映在染色体的『基因』位置就是该染色体的第一个『基因』。）

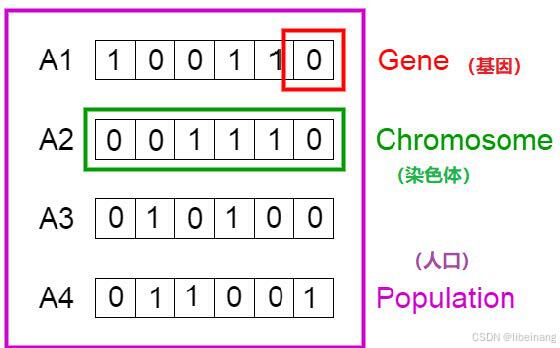
现在，我们将图中的 4 条染色体看作我们的总体初始值。

5.2 适应度函数

接下来，让我们来计算一下前两条染色体的适应度分数。对于 A1 染色体 [100110] 而言，有：

物品项	物品重量	对应生存点数
睡袋	15	15
手电筒	5	5
瓶子	9	8
葡萄糖	29	28

类似地，对于 A2 染色体 [001110] 来说，有：

物品项	物品重量	对应生存点数
皮刀	2	10
手电筒	5	5
瓶子	9	8
总	16	23

对于这个问题，我们认为，当染色体包含更多生存分数时，也就意味着它的适应性更强。
因此，由图可知，染色体 1 适应性强于染色体 2。

5.3 选择

现在，我们可以开始从总体中选择适合的染色体，来让它们互相『交配』，产生自己的下一代了。这个是进行选择操作的大致想法，但是这样将会导致染色体在几代之后相互差异减小，失去了多样性。因此，我们一般会进行「轮盘赌选择法」（Roulette Wheel Selection method）。

想象有一个轮盘，现在我们将它分割成 m 个部分，这里的 m 代表我们总体中染色体的个数。每条染色体在轮盘上占有的区域面积将根据适应度分数成比例表达出来。

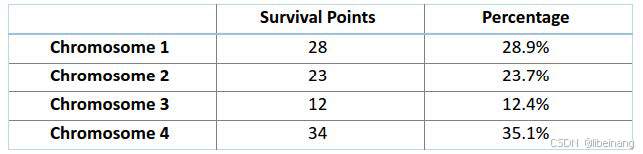
基于上图中的值，我们建立如下「轮盘」。

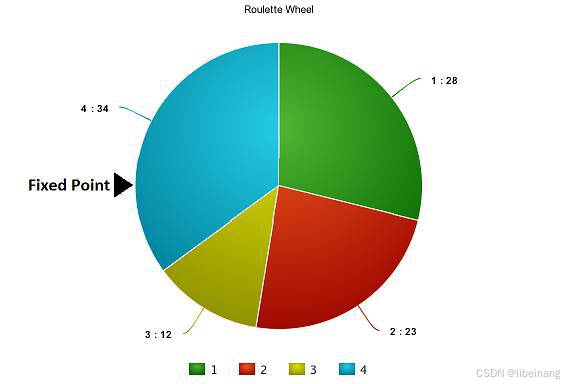
现在，这个轮盘开始旋转，我们将被图中固定的指针（fixed point）指到的那片区域选为第一个亲本。然后，对于第二个亲本，我们进行同样的操作。有时候我们也会在途中标注两个固定指针，如下图：

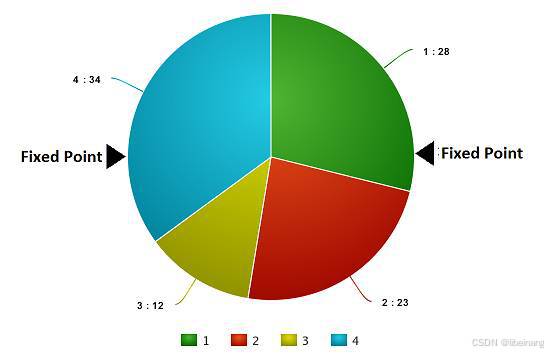
通过这种方法，我们可以在一轮中就获得两个亲本。我们将这种方法成为「随机普遍选择法」（Stochastic Universal Selection method）。

5.4 交叉

在上一个步骤中，我们已经选择出了可以产生后代的亲本染色体。那么用生物学的话说，所谓「交叉」，其实就是指的繁殖。现在我们来对染色体 1 和 4（在上一个步骤中选出来的）进行「交叉」，见下图：

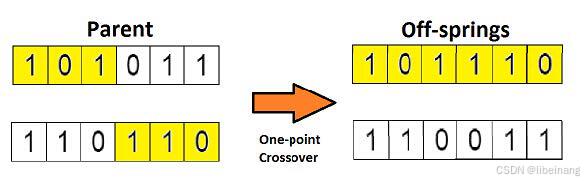
这是交叉最基本的形式，我们称其为「单点交叉」。这里我们随机选择一个交叉点，然后，将交叉点前后的染色体部分进行染色体间的交叉对调，于是就产生了新的后代。

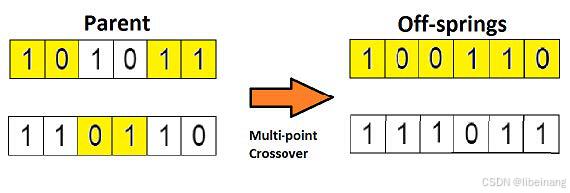
如果你设置两个交叉点，那么这种方法被成为「多点交叉」，见下图：

5.5 变异

如果现在我们从生物学的角度来看这个问题，那么请问：由上述过程产生的后代是否有和其父母一样的性状呢？答案是否。在后代的生长过程中，它们体内的基因会发生一些变化，使得它们与父母不同。这个过程我们称为「变异」，它可以被定义为染色体上发生的随机变化，正是因为变异，种群中才会存在多样性。
下图为变异的一个简单示例：

变异完成之后，我们就得到了新为个体，进化也就完成了，整个过程如下图：

在进行完一轮「遗传变异」之后，我们用适应度函数对这些新的后代进行验证，如果函数判定它们适应度足够，那么就会用它们从总体中替代掉那些适应度不够的染色体。这里有个问题，我们最终应该以什
么标准来判断后代达到了最佳适应度水平呢？
一般来说，有如下几个终止条件：

1. 在进行 X 次迭代之后，总体没有什么太大改变。
2. 我们事先为算法定义好了进化的次数。
3. 当我们的适应度函数已经达到了预先定义的值。

好了，现在我假设你已基本理解了遗传算法的要领，那么现在让我们应用一番。

五、实验步骤

导入库

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D  # matplotlib 的3D绘图工具

实现遗传算法

class GeneticAlgorithm:
    def __init__(self):
        self.len_DNA = 30
        self.len_pop = 300
        self.cross_rate = 0.9
        self.mutate_rate = 0.006
        self.generate_num = 60
        self.range_x = [-5, 5]
        self.range_y = [-5, 5]


    def fun(self, x, y):
        return 5 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1.5) ** 2) - 15 * (x / 8 - x ** 3 - y ** 5) * np.exp(
            -x ** 2 - y ** 2) + (2 - x) ** 2 * np.exp(-(x ** 2))+3 * (x / 8 - x ** 3 - y ** 5) * np.exp(
            -x ** 2 - y ** 2)


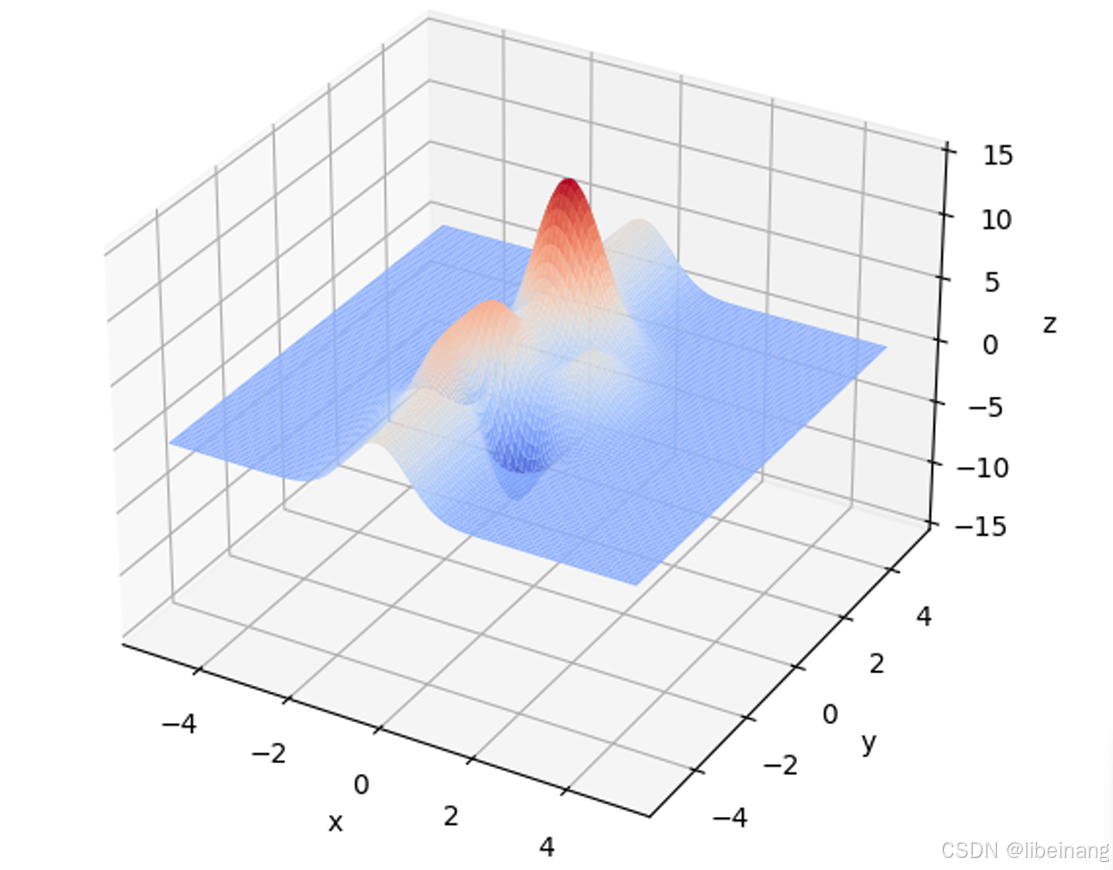
    def plot_3D(self, ax):
        X = np.linspace(*self.range_x, 100)
        Y = np.linspace(*self.range_y, 100)
        X, Y = np.meshgrid(X, Y)
        Z = self.fun(X, Y)
        ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
        ax.set_zlim(-15, 15)
        ax.set_xlabel('x')
        ax.set_ylabel('y')
        ax.set_zlabel('z')
        plt.pause(3)
        plt.show()


    def fitting(self, pop):
        '''
        (pred - np.min(pred))减去最小的适应度是防止出现负数
        + 1e-3防止出现0。
        '''
        x, y = self.translateDNA(pop)
        pred = self.fun(x, y)
        return (pred - np.min(pred)) + 1e-3


    def translateDNA(self, pop):  # pop
        '''
        :param pop: 是种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
        :return:
        '''
        x_pop = pop[:, 1::2]
        y_pop = pop[:, ::2]

        x = x_pop.dot(2 ** np.arange(self.len_DNA)[::-1]) / float(2 ** self.len_DNA - 1) * (self.range_x[1] - self.range_x[0]) + self.range_x[0]
        y = y_pop.dot(2 ** np.arange(self.len_DNA)[::-1]) / float(2 ** self.len_DNA - 1) * (self.range_y[1] - self.range_y[0]) + self.range_y[0]
        return x, y


    def crosso_mul(self, pop, cross_rate=0.8):
        new_pop = []
        # 遍历种群中的每一个个体，将该个体作为父类
        for father in pop:
            #子类先得到父类的基因
            child = father
            # 产生子类时不一定要交叉，是有概率发生的
            if np.random.rand() < cross_rate:
                # 在种群中选择另一个个体，该个体作为母类
                mother = pop[np.random.randint(self.len_pop)]
                # 随机产生交叉点
                cross_points = np.random.randint(low=0, high=self.len_DNA * 2)
                # 子类得到位于交叉点后母类的基因
                child[cross_points:] = mother[cross_points:]
            # 每个子代有机率发生变异
            self.mul(child)  
            new_pop.append(child)

        return new_pop


    def mul(self, child, mutate_rate=0.003):
        # 设定值的概率进行变异
        if np.random.rand() < mutate_rate:  
            # 产生随机一个实数，代表要变异基因的位置
            mutate_point = np.random.randint(0, self.len_DNA)  
             # 反转变异点的二进制
            child[mutate_point] = child[mutate_point] ^ 1 


    def sel(self, pop, fitness):
        idx = np.random.choice(np.arange(self.len_pop), size=self.len_pop, replace=True,
                               p=(fitness) / (fitness.sum()))
        return pop[idx]


    def final_output(self, pop):
        fitness = self.fitting(pop)
        max_fitness_index = np.argmax(fitness)
        print("max_fitness:", fitness[max_fitness_index])
        x, y = self.translateDNA(pop)
        print("最优基因：", pop[max_fitness_index])
        print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))

绘图

#　Axes3D在notebook中不友好，建议在pycharm中查看动态效果
genetic_algorithm = GeneticAlgorithm()
fig = plt.figure()
ax = Axes3D(fig)
plt.ion()
genetic_algorithm.plot_3D(ax)

pop = np.random.randint(2, size=(genetic_algorithm.len_pop, genetic_algorithm.len_DNA*2))
for _ in range(genetic_algorithm.generate_num):
    x,y = genetic_algorithm.translateDNA(pop)
    if 'sca' in locals():
        sca.remove()
    sca = ax.scatter(x, y, genetic_algorithm.fun(x,y), c='black', marker='o')
    plt.show()
    plt.pause(0.1)
    pop = np.array(genetic_algorithm.crosso_mul(pop, genetic_algorithm.cross_rate))
    fitness = genetic_algorithm.fitting(pop)
    # 选择生成新的种群
    pop = genetic_algorithm.sel(pop, fitness)

genetic_algorithm.final_output(pop)
plt.ioff()
genetic_algorithm.plot_3D(ax)

输出结果

	max_fitness: 0.010027197519355213
	最优基因： [1 0 0 1 1 1 0 1 0 1 1 1 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 1 0 0 1 1 0
	 1 1 1 1 0 0 0 0 0 1 1 1 1 0 1 1 1 1 0 0 1 1 1]
	(x, y): (np.float64(-0.15114669236461342), np.float64(1.5624008854500957))

六、实验总结

遗传算法在真实世界中有很多应用，以下列举了部分有趣的场景：

• 工程设计

工程设计非常依赖计算机建模以及模拟，这样才能让设计周期过程即快又经济。遗传算法在这里可以进行优化并给出一个很好的结果。
论文：Engineering design using genetic algorithms
论文地址

• 交通与船运路线（Travelling Salesman Problem，巡回售货员问题）

这是一个非常著名的问题，它已被很多贸易公司用来让运输更省时、经济。解决这个问题也要用到遗传算法。

• 机器人

遗传算法在机器人领域中的应用非常广泛。实际上，目前人们正在用遗传算法来创造可以像人类一样行动的自主学习机器人，其执行的任务可以是做饭、洗衣服等等。
论文：Genetic Algorithms for Auto-tuning Mobile Robot Motion Control
论文地址