神经网络理论知识

感知器：

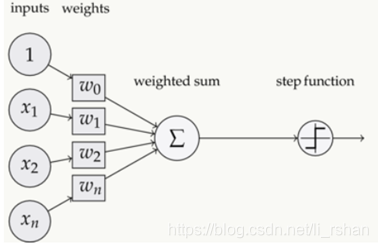
一个感知器有如下组成部分：
输入权值——一个感知器可以接收多个输入（x1,x2,…xn），每个输入上有一个权值wi，此外还有一个偏置项b，就是上图中的w0。
激活函数——感知器的激活函数可以有很多选择
输出——感知器的输出由某个公式来计算
事实上，感知器不仅仅能实现简单的布尔运算。它可以拟合任何的线性函数，任何线性分类或线性回归问题都可以用感知器来解决。前面的布尔运算可以看作是二分类问题，即给定一个输入，输出0（属于分类0）或1（属于分类1）。然而，感知器却不能实现异或运算。

感知器的训练

训练感知器对于多层感知器的监督式训练最常见的深度学习算法是反向传播。基本的过程是 ：
　　1、将训练样本通过神经网络进行前向传播计算。
　　2、计算输出误差，通常用均方差：
　　其中 t 是目标值，y是实际的神经网络输出。其它的误差计算方法也可以，但MSE（均方差）通常是一种比较好的选择。
　　3.网络误差通过随机梯度下降法来最小化。
前面的权重项和偏置项的值是如何获得的呢？
这就要用到感知器训练算法：将权重项和偏置项初始化为0，然后，利用下面的感知器规则迭代的修改wi和b，直到训练完成。

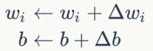
其中：

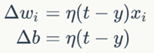
wi是与输入xi对应的权重项，b是偏置项。事实上，可以把b看作是值永远为1的输入xb所对应的权重。t是训练样本的实际值，一般称之为label。而y是感知器的输出值，它是根据公式(1)计算得出。η是一个称为学习速率的常数，其作用是控制每一步调整权的幅度。

每次从训练数据中取出一个样本的输入向量x，使用感知器计算其输出y，再根据上面的规则来调整权重。每处理一个样本就调整一次权重。经过多轮迭代后（即全部的训练数据被反复处理多轮），就可以训练出感知器的权重，使之实现目标函数。
（简单感知器实现and运算）

**

神经网络实际上就是将感知器进行组合，用不同的方式进行连接并作用在不同的激活函数上

**

激活函数

所谓激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。
几种常用激活函数：
1. sigmod函数
函数公式和图表如下图


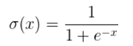
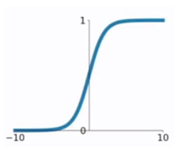
在sigmod函数中我们可以看到，其输出是在(0,1)这个开区间内，可以联想到概率，但是严格意义上不要当成概率。sigmod函数可以想象成一个神经元的放电率，在中间斜率比较大的地方是神经元的敏感区，在两边斜率很平缓的地方是神经元的抑制区。函数本身是有一定的缺陷的。

1. 当输入稍微远离了坐标原点，函数的梯度就变得很小了，几乎为零。在神经网络反向传播的过程中，都是通过微分的链式法则来计算各个权重w的微分的。当反向传播经过了sigmod函数，这个链条上的微分就很小很小了，况且还可能经过很多个sigmod函数，最后会导致权重w对损失函数几乎没影响，这样不利于权重的优化，这个问题叫做梯度饱和，梯度弥散。
2. 函数输出不是以0为中心的，这样会使权重更新效率降低。
3. sigmod函数要进行指数运算，这个对于计算机来说是比较慢的。

2.tanh函数