基于C&CG算法的双目标优化研究：两阶段微电网鲁棒优化代码在MATLAB环境下的求解

两阶段微电网鲁棒优化代码
分别以投资成本和运行成本为目标
采用C&CG算法将模型分为主问题和子问题
用KKT条件将双层模型进行转化
使用MATLAB环境下的yalmip+cplex进行求解

ID:9880664700201770

圣西罗不可思议

---

在当前的能源危机和环境保护的背景下，微电网作为一种可持续发展和高效利用能源的解决方案，受到了广泛的关注和研究。为了在微电网中实现能源资源的优化配置和管理，我们提出了一种基于两阶段优化的鲁棒方法。本文着重介绍了这种方法的代码实现和求解技术。

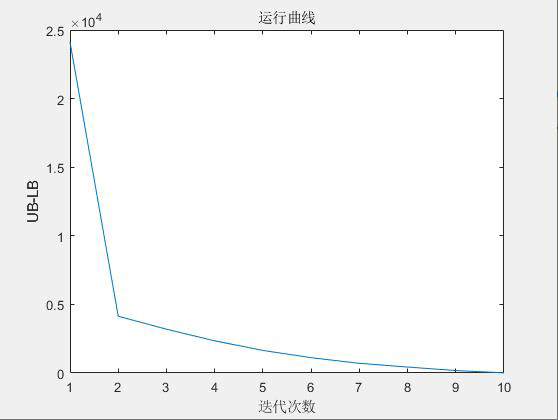
首先，我们将微电网优化问题分为两个阶段，分别以投资成本和运行成本为优化目标。在第一阶段，我们考虑投资成本最小化的问题。通过建立数学模型，我们将微电网的投资决策问题转化为一个规划问题，并采用C&CG算法将其分解为一个主问题和多个子问题。主问题负责确定微电网的总体投资策略，而子问题则负责确定每个具体设备的投资规模。通过迭代求解主问题和子问题，我们可以逐步逼近全局最优解。

在第二阶段，我们考虑运行成本最小化的问题。同样地，我们将微电网的运行优化问题转化为一个规划问题，并采用KKT条件将双层模型进行转化。通过建立运行模型和约束条件，我们可以使用MATLAB环境下的yalmip+cplex工具包进行求解。该工具包结合了优化算法和数学规划技术，能够高效地求解复杂的非线性优化问题。

通过将投资成本和运行成本的优化问题结合起来，我们可以实现微电网在长期和短期两个时间尺度上的鲁棒优化。长期优化可以帮助决策者制定合理的投资计划，优化微电网的能源配置和设备选型。短期优化可以帮助操作人员实时调整微电网的运行策略，以适应不同的负荷需求和能源供应状况。通过综合考虑投资成本和运行成本，我们可以在保证微电网可靠性和稳定性的前提下，最大程度地降低经济成本和能源浪费。

综上所述，基于两阶段微电网鲁棒优化代码的实现，可以通过分别考虑投资成本和运行成本的优化问题，达到最优的经济效益和环境效益。采用C&CG算法和KKT条件进行模型分解和转化，以及使用MATLAB环境下的yalmip+cplex工具包进行求解，可以实现快速而准确的优化结果。这种方法的代码实现和求解技术在微电网的设计和运行中具有广泛的应用前景，对于推动微电网的发展和应用具有重要的意义。

以上相关代码,程序地址：http://matup.cn/664700201770.html