矩阵乘法和逆矩阵

首先说两句非常重要的话，矩阵乘法的基础。
一个矩阵A乘以一个列向量相当于将A的不同列进行线性组合。
一个行向量乘以一个矩阵A相当于将A的不同行进行线性组合。
矩阵乘法的5种方法：

1.

最基本的，AB=C，A的第一行乘以B的第一列得到的便是C的第一行第一列的数，也就是行跟列的点积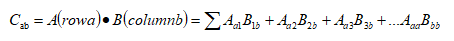（这打出来好麻烦）
接着也就是运用开始说的那两句话

2.

用列的形式看待，举例

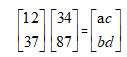
可以将其分别写成

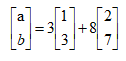
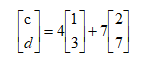
3.

用行的形式看待，举例
还是上面的式子换种写法：


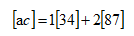
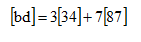
上面三种方法都是把乘式第一个矩阵当做行的形式看待，第二个矩阵看做列，第四种方法用列乘行的形式

4.

例：

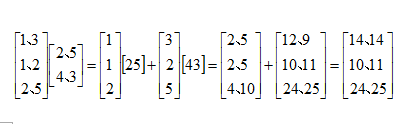
这个可以跟第一种方法做个对比。

5.

用分块矩阵的方法来求，将矩阵分成几块

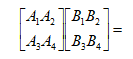
接下来就用第一种方法来求。（待完善）

非可逆矩阵（奇异矩阵）情况：
1.A*X=0,X为一个非零矩阵。
解释：假设A可逆，若在上述式子的左侧乘以一个A-1（A的逆矩阵），那么就会得到X为0矩阵，那反过来说，如果X不为0矩阵，不就代表A不可逆了吗
2.非可逆矩阵的行列式是为0的，这也是比较简单验证的一种方法。
可逆（invertible），非奇异（non-singular）矩阵
如何求可逆矩阵？
其实很简单，采用增广矩阵的方法：
设A为

将其写成增广矩阵的形式，也就是

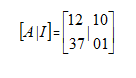
经过一系列消元转换，将左侧左侧变为单位矩阵，右侧得到的便是A的逆矩阵

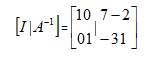
解释;为什么这样得到的就是A的可逆矩阵呢？
在将A转换为单位矩阵过程中进行的是消元转换，每一步的消元都相当于乘以一个消元矩阵，整体乘在一起，我们把它看做E，也就是EA=I,那么E不就是A的逆矩阵了吗，最初增广矩阵右侧I，也是经过消元变换变为我们要的结果，也就是EI=E=A-1，所以这就是我们用这个方法的原因，

逆矩阵一定是一个方阵。（在后面学习矩阵的基时有稍微应用到的地方）

respect to Gauss&Jordan