机器学习模型总结-优快云博客

本文链接：https://blog.youkuaiyun.com/leitouguan8655/article/details/136440217

本文介绍了多种机器学习算法，包括多元线性回归、逻辑回归、决策树等。阐述了各算法的思想、适用数据类型、评测方式、划分方法、剪枝方法等内容，还提及了部分算法的求解方式、后续补充要点，如手动推导、降低计算开销等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

多元线性回归（linear regression）

自变量：连续型数据，因变量：连续型数据
选自：周志华老师《机器学习》P53-55
思想：残差平方和达到最小时的关系式子即为所求，残差平方和：实际值和估计值之间差的平方和。
后续补充：求解方式1：手动推导，求解方式2：梯度下降。手动推到时矩阵不可逆如何加归纳偏好。

残差平方和达到最小：

逻辑回归（logistic regression）

以下选自：王汉生《应用商务统计分析》第四章
（1）变量：连续型数据，因变量：离散型数据
（2）思想：假设了一个式子，计算事件发生的可能性。
令事件发生的可能性用Z表示：

设定一个阈值c,使得：

无论对F(t)的具体函数形式作任何假设,该假设都不可能完全反映真实情形,那么挑选那些“方便"的假设，假设服从正态分布。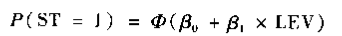，该模型称为probit模型，但是很多年前计算不够发达的时候，这种假设过于复杂，计算不出来，所以便产生了如下的公式：

（3）效果评测方式：
TPR：召回率，有问题的预测为有问题的比例，即预测出来有问题的个数/所有有问题的个数：TP/(TP+FN)
FPR：误报，FP/(TN+FP)，将正常的预测为有问题的数/所有正常的个数
**同一个模型，找效果最好时的阈值：**设置不同的阈值后可以绘制ROC曲线，然后选取自己想要的召回率和误报平衡组合。ROC曲线同对角线(虚线)相比,永远是向