《深入浅出搜索架构(上篇)》

转自：点击打开链接http://zhuanlan.51cto.com/art/201702/531315.htm

四、搜索原理与核心数据结构

• 什么是正排索引?
• 什么是倒排索引?
• 搜索的过程是什么样的?
• 会用到哪些算法与数据结构?

前面的内容太宏观，为了照顾大部分没有做过搜索引擎的同学，数据结构与算法部分从正排索引、倒排索引一点点开始。

提问：什么是正排索引(forward index)?

回答：由key查询实体的过程，是正排索引。

用户表：t_user(uid, name, passwd, age, sex)，由uid查询整行的过程，就是正排索引查询。

网页库：t_web_page(url, page_content)，由url查询整个网页的过程，也是正排索引查询。

网页内容分词后，page_content会对应一个分词后的集合list。

简易的，正排索引可以理解为Map

提问：什么是倒排索引(inverted index)?

回答：由item查询key的过程，是倒排索引。

对于网页搜索，倒排索引可以理解为Map

举个例子，假设有3个网页：

url1 -> “我爱北京”

url2 -> “我爱到家”

url3 -> “到家美好”

这是一个正排索引Map

分词之后：

url1 -> {我，爱，北京}

url2 -> {我，爱，到家}

url3 -> {到家，美好}

这是一个分词后的正排索引Map

分词后倒排索引：

我 -> {url1, url2}

爱 -> {url1, url2}

北京 -> {url1}

到家 -> {url2, url3}

美好 -> {url3}

由检索词item快速找到包含这个查询词的网页Map

正排索引和倒排索引是spider和build_index系统提前建立好的数据结构，为什么要使用这两种数据结构，是因为它能够快速的实现“用户网页检索”需求(业务需求决定架构实现)。

提问：搜索的过程是什么样的?

假设搜索词是“我爱”，用户会得到什么网页呢?

(1)分词，“我爱”会分词为{我，爱}，时间复杂度为O(1)

(2)每个分词后的item，从倒排索引查询包含这个item的网页list，时间复杂度也是O(1)：

我 -> {url1, url2}

爱 -> {url1, url2}

(3)求list的交集，就是符合所有查询词的结果网页，对于这个例子，{url1, url2}就是最终的查询结果

看似到这里就结束了，其实不然，分词和倒排查询时间复杂度都是O(1)，整个搜索的时间复杂度取决于“求list的交集”，问题转化为了求两个集合交集。

字符型的url不利于存储与计算，一般来说每个url会有一个数值型的url_id来标识，后文为了方便描述，list统一用list替代。

提问：list1和list2，求交集怎么求?

方案一：for * for，土办法，时间复杂度O(n*n)

每个搜索词命中的网页是很多的，O(n*n)的复杂度是明显不能接受的。倒排索引是在创建之初可以进行排序预处理，问题转化成两个有序的list求交集，就方便多了。

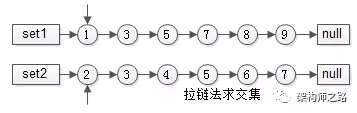
方案二：有序list求交集，拉链法

有序集合1{1,3,5,7,8,9}

有序集合2{2,3,4,5,6,7}

两个指针指向首元素，比较元素的大小：

(1)如果相同，放入结果集，随意移动一个指针

(2)否则，移动值较小的一个指针，直到队尾

这种方法的好处是：

(1)集合中的元素最多被比较一次，时间复杂度为O(n)

(2)多个有序集合可以同时进行，这适用于多个分词的item求url_id交集

这个方法就像一条拉链的两边齿轮，一一比对就像拉链，故称为拉链法

方案三：分桶并行优化

数据量大时，url_id分桶水平切分+并行运算是一种常见的优化方法，如果能将list1和list2分成若干个桶区间，每个区间利用多线程并行求交集，各个线程结果集的并集，作为最终的结果集，能够大大的减少执行时间。

举例：

• 有序集合1{1,3,5,7,8,9, 10,30,50,70,80,90}
• 有序集合2{2,3,4,5,6,7, 20,30,40,50,60,70}

求交集，先进行分桶拆分：

• 桶1的范围为[1, 9]
• 桶2的范围为[10, 100]
• 桶3的范围为[101, max_int]

于是：

集合1就拆分成

• 集合a{1,3,5,7,8,9}
• 集合b{10,30,50,70,80,90}
• 集合c{}
• 集合2就拆分成
• 集合d{2,3,4,5,6,7}
• 集合e{20,30,40,50,60,70}
• 集合e{}

每个桶内的数据量大大降低了，并且每个桶内没有重复元素，可以利用多线程并行计算：

• 桶1内的集合a和集合d的交集是x{3,5,7}
• 桶2内的集合b和集合e的交集是y{30, 50, 70}
• 桶3内的集合c和集合d的交集是z{}

最终，集合1和集合2的交集，是x与y与z的并集，即集合{3,5,7,30,50,70}

方案四：bitmap再次优化

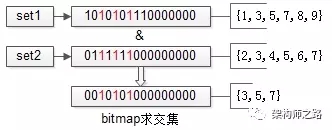
数据进行了水平分桶拆分之后，每个桶内的数据一定处于一个范围之内，如果集合符合这个特点，就可以使用bitmap来表示集合：

如上图，假设set1{1,3,5,7,8,9}和set2{2,3,4,5,6,7}的所有元素都在桶值[1, 16]的范围之内，可以用16个bit来描述这两个集合，原集合中的元素x，在这个16bitmap中的第x个bit为1，此时两个bitmap求交集，只需要将两个bitmap进行“与”操作，结果集bitmap的3，5，7位是1，表明原集合的交集为{3,5,7}

水平分桶，bitmap优化之后，能极大提高求交集的效率，但时间复杂度仍旧是O(n)

bitmap需要大量连续空间，占用内存较大

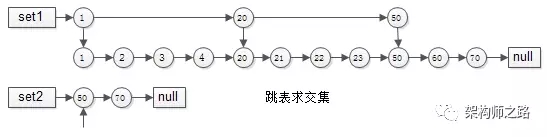
方案五：跳表skiplist

有序链表集合求交集，跳表是最常用的数据结构，它可以将有序集合求交集的复杂度由O(n)降至O(log(n))

• 集合1{1,2,3,4,20,21,22,23,50,60,70}
• 集合2{50,70}

要求交集，如果用拉链法，会发现1,2,3,4,20,21,22,23都要被无效遍历一次，每个元素都要被比对，时间复杂度为O(n)，能不能每次比对“跳过一些元素”呢?

跳表就出现了：

• 集合1{1,2,3,4,20,21,22,23,50,60,70}建立跳表时，一级只有{1,20,50}三个元素，二级与普通链表相同
• 集合2{50,70}由于元素较少，只建立了一级普通链表

如此这般，在实施“拉链”求交集的过程中，set1的指针能够由1跳到20再跳到50，中间能够跳过很多元素，无需进行一一比对，跳表求交集的时间复杂度近似O(log(n))，这是搜索引擎中常见的算法。