强化学习玩21点

sutton RL an introduction 2nd CH5例子
ref:
https://github.com/ShangtongZhang/reinforcement-learning-an-introduction/edit/master/chapter05/blackjack.py
本文解读整理上述示例代码

规则

21点（blackjack）是经典赌场游戏，玩的是在牌面和不超过21点的情况下尽可能大。牌面规定：Ace可以是1 或 11， J,Q,K均为10，无大小王。具体规则有很多种，书中规定如下：

The object of the popular casino card game of blackjack is to obtain cards the sum of whose numerical values is as great as possible without exceeding 21. All face cards count as 10, and an ace can count either as 1 or as 11. We consider the version in which each player competes independently against the dealer. The game begins with two cards dealt to both dealer and player. One of the dealer’s cards is face up and the other is face down. If the player has 21 immediately (an ace and a 10-card), it is called a natural. He then wins unless the dealer also has a natural, in which case the game is a draw. If the player does not have a natural, then he can request additional cards, one by one (hits), until he either stops (sticks) or exceeds 21 (goes bust ). If he goes bust, he loses; if he sticks, then it becomes the dealer’s turn. The dealer hits or sticks according to a fixed strategy without choice: he sticks on any sum of 17 or greater, and hits otherwise. If the dealer goes bust, then the player wins; otherwise, the outcome—win, lose, or draw—is determined by whose final sum is closer to 21.

首先是21点游戏逻辑的定义和一些预设policy。
作为玩家，只有hit 和 stand两种action
其进行决策只需考虑如下三点：

1. usable_ace手头是否有ace牌，且能叫为11点而不爆牌
2. 手头牌面值和（12-21）0-11不需考虑，因为无论抽到什么牌怎么都不可能爆牌，故一定是hit
3. 庄家的明牌。(1,…10)（J Q K都是10）
   所以共有2*10*10 200个state，故policy表和value表就是2*10*10的

import numpy as np
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm

# actions: hit or stand
ACTION_HIT = 0
ACTION_STAND = 1  #  "strike" in the book
ACTIONS = [ACTION_HIT, ACTION_STAND]

# policy for player
# 这是书中规定的一个policy，用于演示MC policy evaluation，
# 其很朴素，只在自己牌面和为 20 or 21 时stand，其余一律hit，不考虑其他因素
POLICY_PLAYER = np.zeros(22, dtype=np.int)
for i in range(12, 20):
    POLICY_PLAYER[i] = ACTION_HIT
POLICY_PLAYER[20] = ACTION_STAND
POLICY_PLAYER[21] = ACTION_STAND

###########这俩policy是为off-policy算法准备 
# function form of target policy of player
def target_policy_player(usable_ace_player, player_sum, dealer_card):
    return POLICY_PLAYER[player_sum]

# function form of behavior policy of player
def behavior_policy_player(usable_ace_player, player_sum, dealer_card):
    if np.random.binomial(1, 0.5) == 1:
        return ACTION_STAND
    return ACTION_HIT
###########
# policy for dealer
# 21点游戏规则规定的庄家policy，即持续hit直至>=17
POLICY_DEALER = np.zeros(22)
for i in range(12, 17):
    POLICY_DEALER[i] = ACTION_HIT
for i in range(17, 22):
    POLICY_DEALER[i] = ACTION_STAND

# get a new card
def get_card():
    card = np.random.randint(1, 14)# [1,14)
    card = min(card, 10)#（J Q K都是10）
    return card

# get the value of a card (11 for ace).
def card_value(card_id):
    return 11 if card_id == 1 else card_id

# play a game 环境交互核心函数，返回：
#（state, reward, player_trajectory）
# 其中state = [usable_ace_player, player_sum, dealer_card1]
#     reward 是+1 或-1或0
#     player_trajectory [(usable_ace_player, player_sum, dealer_card1), action])的
#     序列

# @policy_player: specify policy for player
# @initial_state: [whether player has a usable Ace, sum of player's cards, one card of dealer]
# @initial_action: the initial action
def play(policy_player, initial_state=None, initial_action=None):
    # player status

    # sum of player
    player_sum = 0

    # trajectory of player
    player_trajectory = []

    # whether player uses Ace as 11
    usable_ace_player = False

    # dealer status
    dealer_card1 = 0
    dealer_card2 = 0
    usable_ace_dealer = False

    if initial_state is None:
        # generate a random initial state

        while player_sum < 12:
            # if sum of player is less than 12, always hit
            card = get_card()
            player_sum += card_value(card)

            # If the player's sum is larger than 21, he may hold one or two aces.
            if player_sum > 21:
                assert player_sum == 22
                # last card must be ace
                player_sum -= 10
            else:
                usable_ace_player |= (1 == card)

        # initialize cards of dealer, suppose dealer will show the first card he gets
        dealer_card1 = get_card()
        dealer_card2 = get_card()

    else:
        # use specified initial state
        usable_ace_player, player_sum, dealer_card1 = initial_state
        dealer_card2 = get_card()

    # initial state of the game
    state = [usable_ace_player, player_sum, dealer_card1]

    # initialize dealer's sum
    dealer_sum = card_value(dealer_card1) + card_value(dealer_card2)
    usable_ace_dealer = 1 in (dealer_card1, dealer_card2)
    # if the dealer's sum is larger than 21, he must hold two aces.
    if dealer_sum > 21:
        assert dealer_sum == 22
        # use one Ace as 1 rather than 11
        dealer_sum -= 10
    assert dealer_sum <= 21
    assert player_sum <= 21

    # game starts!

    # player's turn
    while True:
        if initial_action is not None:
            action = initial_action
            initial_action = None
        else:
            # get action based on current sum
            action = policy_player(usable_ace_player, player_sum, dealer_card1)

        # track player's trajectory for importance sampling
        player_trajectory.append([(usable_ace_player, player_sum, dealer_card1), action])

        if action == ACTION_STAND:
            break
        # if hit, get new card
        card = get_card()
        # Keep track of the ace count. the usable_ace_player flag is insufficient alone as it cannot
        # distinguish between having one ace or two.
        ace_count = int(usable_ace_player)
        if card == 1:
            ace_count += 1
        player_sum += card_value(card)
        # If the player has a usable ace, use it as 1 to avoid busting and continue.
        while player_sum > 21 and ace_count:
            player_sum -= 10
            ace_count -= 1
        # player busts
        if player_sum > 21:
            return state, -1, player_trajectory
        assert player_sum <= 21
        usable_ace_player = (ace_count == 1)

    # dealer's turn
    while True:
        # get action based on current sum
        action = POLICY_DEALER[dealer_sum]
        if action == ACTION_STAND:
            break
        # if hit, get a new card
        new_card = get_card()
        ace_count = int(usable_ace_dealer)
        if new_card == 1:
            ace_count += 1
        dealer_sum += card_value(new_card)
        # If the dealer has a usable ace, use it as 1 to avoid busting and continue.
        while dealer_sum > 21 and ace_count:
            dealer_sum -= 10
            ace_count -= 1
        # dealer busts
        if dealer_sum > 21:
            return state, 1, player_trajectory
        usable_ace_dealer = (ace_count == 1)

    # compare the sum between player and dealer
    assert player_sum <= 21 and dealer_sum <= 21
    if player_sum > dealer_sum:
        return state, 1, player_trajectory
    elif player_sum == dealer_sum:
        return state, 0, player_trajectory
    else:
        return state, -1, player_trajectory

蒙特卡洛 policy 评估

该方法是对无完整过程模型p，无法使用DP，而仅从交互序列中进行值函数v(s)估计的方法。可分为first-visit 和 every-visit两种，其区别在于first-visit仅处理每一个交互序列中某state的第一次出现，而every-visit对每一个交互序列中某state的每次出现一视同仁。
具体做法可由代码进行理解：

# Monte Carlo Sample with On-Policy
def monte_carlo_on_policy(episodes):
    states_usable_ace = np.zeros((10, 10))
    # initialze counts to 1 to avoid 0 being divided
    states_usable_ace_count = np.ones((10, 10))
    states_no_usable_ace = np.zeros((10, 10))
    # initialze counts to 1 to avoid 0 being divided
    states_no_usable_ace_count = np.ones((10, 10))
    for i in tqdm(range(0, episodes)):
        _, reward, player_trajectory = play(target_policy_player)
        for (usable_ace, player_sum, dealer_card), _ in player_trajectory:
            player_sum -= 12 # 因为value表的第一个index是12
            dealer_card -= 1 # 同样是index问题
            if usable_ace:
                states_usable_ace_count[player_sum, dealer_card] += 1
                states_usable_ace[player_sum, dealer_card] += reward
            else:
                states_no_usable_ace_count[player_sum, dealer_card] += 1
                states_no_usable_ace[player_sum, dealer_card] += reward
    return states_usable_ace / states_usable_ace_count, states_no_usable_ace / states_no_usable_ace_count

该函数对前面定义的简单policy进行v(s)评估。将200个state按有无ace分两类分别返回（100+100）。此函数使用every-visit，实践中绝大部分都是every-visit，因为实现更方便，不用验证是不是first-visit。拿到一个交互序列后，遍历其中每一step，将交互序列的reward对应加到各个state上。整个过程重复episodes次，最后对value表用state count求平均。
按此方法即可在未知过程模型的情况下，仅用policy 与 环境的交互结果对policy对应的v(s)进行估计。

Monte Carlo policy iteration with Exploring Starts

上部分主要目的是阐述Monte Carlo 估计RL问题的基本方法。我们要想将Monte Carlo应用到DP中的 policy iteration算法上求optimal policy，需要估计state_action_values 即q(a,s)而非v(s)，这是因为没有过程模型p时，仅有v(s)是无法求optimal action的。（DP中可以）。下面的算法采用greedy policy，并用Exploring Starts弥补探索的缺失。所谓Exploring Starts就是随机选取交互的init，这样在当进行的episodes足够多的时候，就可以保证每个state都被探索到了。显然Exploring Starts在很多实际问题中并不现实，因为init态很多时候是定死的，导致Exploring Starts无法进行，之后会讨论其他保证探索的方法。

# Monte Carlo policy iteration with Exploring Starts
def monte_carlo_es(episodes):
    # (playerSum, dealerCard, usableAce, action)
    state_action_values = np.zeros((10, 10, 2, 2))
    # initialze counts to 1 to avoid division by 0
    state_action_pair_count = np.ones((10, 10, 2, 2))

    # behavior policy is greedy
    # 如遇到value的action则随机选取
    def behavior_policy(usable_ace, player_sum, dealer_card):
        usable_ace = int(usable_ace)
        player_sum -= 12
        dealer_card -= 1
        # get argmax of the average returns(s, a)
        values_ = state_action_values[player_sum, dealer_card, usable_ace, :] / \
                  state_action_pair_count[player_sum, dealer_card, usable_ace, :]
        return np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])

    # play for several episodes
    for episode in tqdm(range(episodes)):
        # for each episode, use a randomly initialized state and action
        # 即Exploring Starts
        # x下面更新q(s,a)表
        initial_state = [bool(np.random.choice([0, 1])),
                         np.random.choice(range(12, 22)),
                         np.random.choice(range(1, 11))]
        initial_action = np.random.choice(ACTIONS)
        current_policy = behavior_policy if episode else target_policy_player
        _, reward, trajectory = play(current_policy, initial_state, initial_action)
        for (usable_ace, player_sum, dealer_card), action in trajectory:
            usable_ace = int(usable_ace)
            player_sum -= 12
            dealer_card -= 1
            # update values of state-action pairs
            state_action_values[player_sum, dealer_card, usable_ace, action] += reward
            state_action_pair_count[player_sum, dealer_card, usable_ace, action] += 1

    return state_action_values / state_action_pair_count

On-Policy 和 Off-Policy

为了能不用Exploring Starts并保证探索，可以采用Chapter2中的e-greedy策略，但这种方法最后收敛得到的value* π*是对e-greedy这个policy的，只是近似最优，为了解决此问题，又发展了一类方法叫off-policy。其使用两个policy，一个target_policy作为目标policy作为最终的policy（一般就是按value greedy的），另一个带探索的behavior_policy用于产生交互序列。off-policy名称的含义即指这种用其他policy的交互数据对本policy进行提升和评估的一类方法。与之相对的on-policy就是形如上面Monte Carlo policy iteration with Exploring Starts的一类方法，仅有一个policy自给自足。
off-policy为了能利用behavior_policy的交互数据为target_policy进行action_value表估计，需要引入importance sampling来进行补偿一面产生biased的估计。
某个policy交互出某一action state序列的概率可表示为：

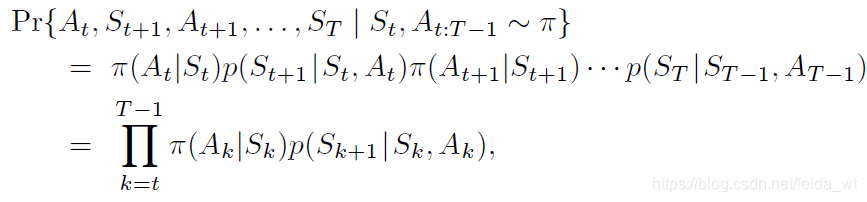
忽略环境p的部分，可推知其importance-sampling-ratio应该是

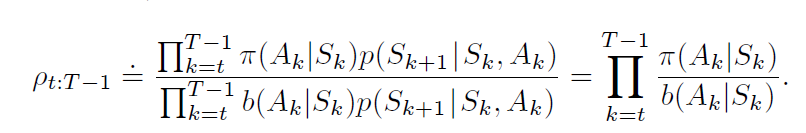
importance-sampling进一步分为ordinary importance sampling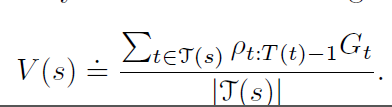
和 weighted importance sampling

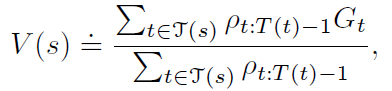
实践上weighted importance sampling更常用。下面的函数同时计算了两类方法。注意importance-sampling-ratio的计算，一旦序列中action出现不同，就会给0，终止计算。（因为错误的action后，p(s|s,a)就会产生出0，既拐不回去了。。）

# Monte Carlo Sample with Off-Policy
def monte_carlo_off_policy(episodes):
    initial_state = [True, 13, 2]

    rhos = []
    returns = []

    for i in range(0, episodes):
        _, reward, player_trajectory = play(behavior_policy_player, initial_state=initial_state)

        # get the importance ratio
        numerator = 1.0
        denominator = 1.0
        for (usable_ace, player_sum, dealer_card), action in player_trajectory:
            if action == target_policy_player(usable_ace, player_sum, dealer_card):
                denominator *= 0.5
            else:
                numerator = 0.0
                break
        rho = numerator / denominator
        rhos.append(rho)
        returns.append(reward)

    rhos = np.asarray(rhos)
    returns = np.asarray(returns)
    weighted_returns = rhos * returns
	# 这里算accumulate是方便后面的误差统计，无关紧要
    weighted_returns = np.add.accumulate(weighted_returns)
    rhos = np.add.accumulate(rhos)

    ordinary_sampling = weighted_returns / np.arange(1, episodes + 1)

    with np.errstate(divide='ignore', invalid='ignore'):
        weighted_sampling = np.where(rhos != 0, weighted_returns / rhos, 0)

    return ordinary_sampling, weighted_sampling