【证明】用快慢指针判断链表中有环、环入口元素，以leetcode287为例子

leetcode题目连接如下287. 寻找重复数 - 力扣（LeetCode）

题目中怎么把数组转成环不解释，只通过数学方法证明找到环入口元素的可行性。

链表中有环

定义两个快慢指针i, j，i步长设置为1，j步长设置为2，那么因为环的缘故，两个指针进入到了环之后就会无限循环，j作为运动快的指针总会追上i的，那么只要j与i所指的值相等了，那就说明有环，这个很好理解。

环的入口元素即为重复的元素

以题目里的测试用例为例子

vector<int> nums = {1,3,4,2,2};

那么我们就可以得到以下的环: 

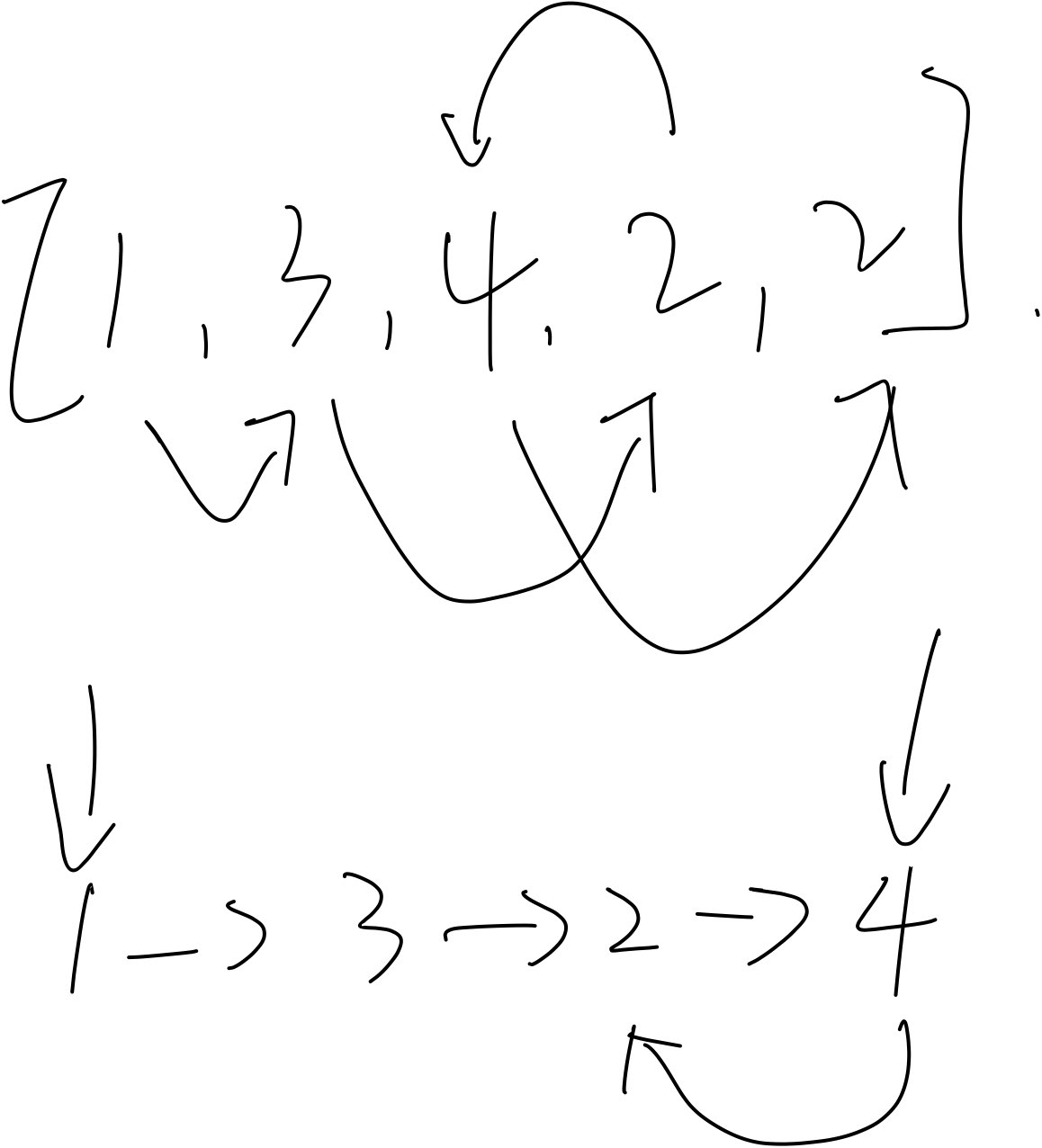
重复的元素会将指针指向重复的位置，到重复的位置之后继续遍历到重复的位置之后就会再回到原点，从而形成环，这个也很好理解。

数学证明：可以找到入口元素

假设有以下的环：

设从起点到环入口点的距离为，快慢指针相遇的位置距离环的起点距离为，环周长为。

由于快指针的速度是慢指针的两倍，那么快行走的距离也是满指针的两倍，所以我们可以得到以下等式：

经过移项化简可以得到等式：

这样看起来不是很明显，再提取出一个出来得到：

前面是系数，可以理解为围绕环转了圈，最后表示从相遇点再移动到环入口点的距离。

以上公式可以理解为，从链表开头到环的入口点的距离，等于从相遇点再围绕环运行圈之后再运行到入口点的距离。

因此，我们只需要在两个指针第一次相遇之后，再设置一个指向链表开头的指针，速度和慢指针相同，那么两个指针就会在环的入口点相遇。

至此就通过数学方法找到了证明环入口点的方法。

代码实现

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast = 0;
        int slow = 0;
        while (1) {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if (slow == fast) {
                fast = 0;
                break;
            }
        }
        while (fast != slow) {
            fast = nums[fast];
            slow = nums[slow];
        }
        return fast;
    }
};

细节问题

我一开始的代码是

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast = 0;
        int slow = 0;
        while (1) {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if (slow == fast) {
                fast = nums[0];
                break;
            }
        }
        while (fast != slow) {
            fast = nums[fast];
            slow = nums[slow];
        }
        return fast;
    }
};

区别就是在第一个循环终止的时候赋值有点不同，但是这个代码提交之后显示运行超时了，最后经过调试发现，快指针好像跑快了，进入环之后就无限循环了。

分析之后发现是因为，实际上的环应该是这样的：

我如果直接将fast赋值为nums[0]就相当于让fast先走了一步，所以要会死循环。把fast一开始赋值为0就行了，或者让slow先走一步在将fast赋值为nums[0]。