全文共988个字,6张图,预计阅读时间8分钟。
一看这个标题就会想,这有什么大惊小怪的,可能好多人觉得这是个脑残话题,但我确实误解了两三年……
今天在读《OpenCV算法精解》的时候,发现对两个矩阵做卷积运算的时候,作为卷积算子的矩阵要逆时针旋转180度,这是以前从来没注意过的步骤, 说来惭愧,平时都是直接调用API,忽略了原理,以为卷积就是像很多图上画的,一个卷积核挨着扫描另一个矩阵,结果叠加起来,当初上数字图像处理课的时候也手算过卷积,不知道是老师讲错了还是我记错了,总之一直都没注意到卷积运算其实是「先翻转再平移」。
维基百科中这样描述卷积的物理意义:
在泛函分析中,卷积、叠积、摺积或旋积,是通过两个函数f和g生成第三个函数的一种数学算子,表征函数f与经过翻转和平移的g的乘积函数所围成的曲边梯形的面积。
连续卷积
数学定义是:
函数f和g是定义在Rn上的可测函数,f与g的卷积记做f*g,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数,也就是:
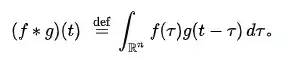
连续卷积公式(From Wikipedia)
知乎上有一个关于「如何通俗易懂地解释卷积」的问答,有很多解释版本,也都通俗易懂,挺有意思,但是个人认为维基百科的下面这张图用于理解卷积已经足够。特别注意圈住的那句话,对理解卷积的意义很有帮助。
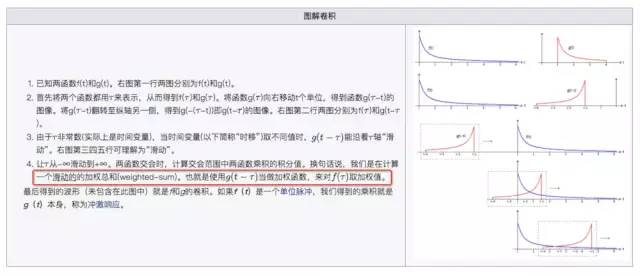
图解卷积(From Wikipedia)
离散卷积

离散卷积(From Wikipedia)
Example
我主要做图像处理,所以用到的是离散卷积。使用python做验证。
下面这个图是我们最常见的卷积运算图:
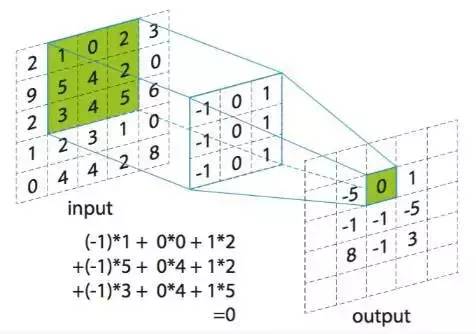
卷积运算图(来自百度图片搜索)
中间的卷积核,其实是已经逆时针旋转过180度的,即做卷积的两个矩阵其实是[[2, 1, 0, 2, 3], [9, 5, 2,4, 2, 0], [2, 3, 4, 5, 6], [1, 2, 3, 1, 0], [0, 4, 4, 2, 8]]和[[1, 0, -1], [1, 0, -1], [1, 0, -1]],没有旋转只有乘积求和就不叫卷积运算。
先来两个矩阵,根据公式手动推导一下:

手算卷积
可以发现,只有卷积核旋转180度再扫描,才会和公式推导计算的结果一样,将I和K矩阵用python做卷积:
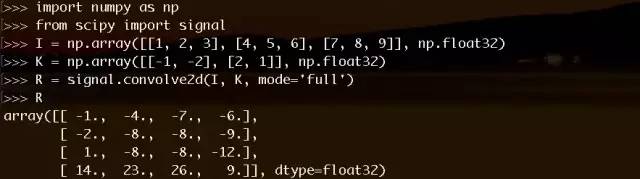
python卷积.png
和我们手算的一样。所以自己做卷积的时候,记得「翻转再平移」……或者干脆用公式计算,至少不会错。
原文链接:https://www.jianshu.com/p/3b3a6743cab7
查阅更为简洁方便的分类文章以及最新的课程、产品信息,请移步至全新呈现的“LeadAI学院官网”:
www.leadai.org
请关注人工智能LeadAI公众号,查看更多专业文章

大家都在看





















 1285
1285

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








