激光SLAM之里程计标定

里程计模型可以分为3类：

• 1.两轮差分底盘的运动型模型
• 2.三轮全向底盘的运动学模型
• 3.航迹推算（Dead Rocking）

航机推算

其中航迹推算的方法是最普遍的，其示意图为

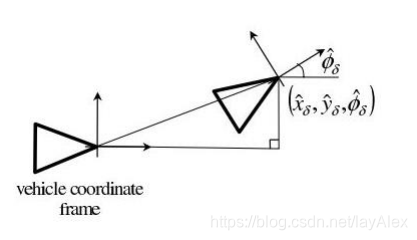
推算公式

• $(x,y,z)$为底盘当前位姿
• $(dx,dy,d\theta )$为运动学解算增量
  $$\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]=\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]+\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}dx\\ dy\\ d\theta \end{array}\right]$$
  由于在工程应用里程计会有误差，所以需要加一个误差,这是一个高斯白噪声
  $$\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]=\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]+\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}dx+{ϵ}_x\\ dy+{ϵ}_y\\ d\theta +{ϵ}_{\theta }\end{array}\right]$$

线性最小二乘

线性最小二乘是一种比较通用的标定方法，但是由于比较通用，所以无法做到性能最佳，一般最优的线性方法都是根据工程项目来特定的，下面来介绍一下最小二乘的一些原理

原理

线性方程组$Ax=b$
𝐴为𝑚 × 𝑛的矩阵。 x为𝑛 × 1的向量
当m=n时，适定方程组，方程组有唯一解
当m<n时，欠定方程组，方程组有无穷多解
当m>n时，超定方程组，方程组有通常无解
但在现实中，绝大多数情况为m>n，比如说我们要求的参数只有两个，而我们需要采集很多组数据，这些数据都存在误差，可能两两之间都是矛盾的，所以超定方程组,无解，可以寻找最靠近真实解的解，无解但是有最小二乘解，通解: $$x^{\ast }=(A^{T}A{)}^{-1}{A}^{T}b$$
那么为什么是这个方程呢？？
我们从线性空间的角度来考虑，假设$Ax$表示$A$的列向量空间$S$，无解意味着向量$b$不在S中，最近的解即为向量$b$在$S$中的投影。
假设$A{x}^{\ast }$为向量$b$在空间$S$中的投影，显然$(b-A{x}^{\ast })$垂直于空间$S$，那么$(b-A{x}^{\ast })$跟矩阵$A$的每一个列向量都垂直
设$$A=\left[\begin{array}{cccc}{a}_1& a_2& ...& a_n\end{array}\right]$$𝑎𝑖表示矩阵A的第i个列向量,则
$$a_i^T(b-A{x}^{\ast })=0$$
可得：$$A^T(b-A{x}^{\ast })=0$$
$$A^{T}b=A^{T}A{x}^{\ast }$$
$$x^{\ast }=(A^{T}A{)}^{-1}{A}^{T}b$$

里程计标定

• 直接线性方法：通用性强，实现简单，精度不高
• 基于模型的方法：精度高，实现复杂，特异性高
  这里介绍一下直接线性方法
  1.用激光雷达的scan-match数据作为真值${\mu }_i^{\ast }$
  2.里程计测量得到的数据为${\mu }_i$
  3.假设成线性关系${\mu }^{\ast }=X\ast {\mu }_i$
  其中：$$X=\left[\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\end{array}\right]$$
  转换方程得$$\left[\begin{array}{cccccccccc}{\mu }_{ix}& {\mu }_{iy}& {\mu }_{i\theta }& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& {\mu }_{ix}& {\mu }_{iy}& {\mu }_{i\theta }& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& {\mu }_{ix}& {\mu }_{iy}& {\mu }_{i\theta }\end{array}\right]\left[\begin{array}{c}{x}_{11}\\ ⋮\\ x_{33}\end{array}\right]=\left[\begin{array}{c}{\mu }_{ix}^{\ast }\\ {\mu }_{iy}^{\ast }\\ {\mu }_{i\theta }^{\ast }\end{array}\right]$$
  其中$$A=\left[\begin{array}{cccccccccc}{\mu }_{ix}& {\mu }_{iy}& {\mu }_{i\theta }& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& {\mu }_{ix}& {\mu }_{iy}& {\mu }_{i\theta }& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& {\mu }_{ix}& {\mu }_{iy}& {\mu }_{i\theta }\end{array}\right]$$
  $$x=\left[\begin{array}{c}{x}_{11}\\ ⋮\\ x_{33}\end{array}\right]$$$$b=\left[\begin{array}{c}{\mu }_{ix}^{\ast }\\ {\mu }_{iy}^{\ast }\\ {\mu }_{i\theta }^{\ast }\end{array}\right]$$