基于sklearn的机器学习 — 支持向量机（SVM）

最新推荐文章于 2025-04-01 06:35:43 发布

基算仿真

最新推荐文章于 2025-04-01 06:35:43 发布

阅读量1.9k

点赞数 32

分类专栏： Python 机器学习文章标签：机器学习 sklearn 支持向量机 python

本文链接：https://blog.youkuaiyun.com/laughzjh/article/details/140977088

版权

支持向量机（SVM：support vector machine）另一种功能强大、应用广泛的学习算法，可应用于分类、回归、密度估计、聚类等问题。SVM可以看作是感知器（可被视为一种最简单形式的前馈神经网络，是一种二元线性分类器）的扩展，与逻辑回归相比，支持向量机在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

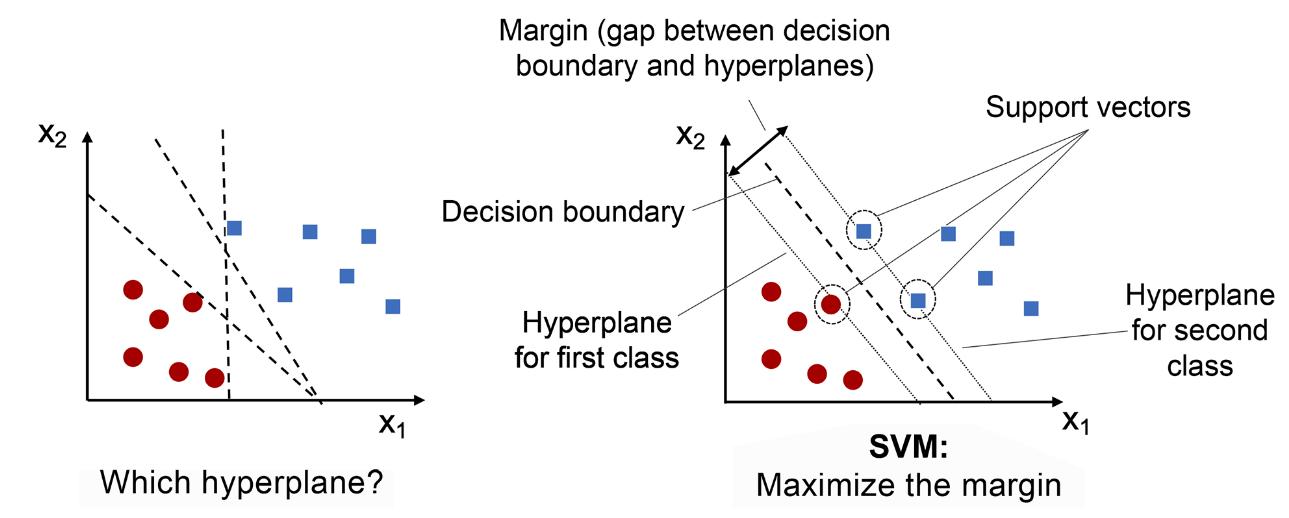
SVM是一种监督式的学习方法，用统计风险最小化的原则来估计一个分类的超平面(hyperplane) ，其基础的概念非常简单，就是找到一个决策边界(decision boundary) ，让两类之间的边界(margins) 最大化，使其可以完美地分隔开来。

超平面(hyperplane) 是n维空间中的n - 1个子空间。例如，想要划分一个二维空间，需要使用一维超平面（即一条线），划分三维空间，需要使用二维超平面（即一张面），超平面只是将这一概念推广到 n 维空间。

不同维度下的超平面

支持向量(support vectors) 指的是最接近超平面或超平面上的数据点，它们影响超平面的位置和方向。

边界(margin) 的定义是：分离超平面（决策边界）与最接近该超平面的训练实例（即支持向量）之间的距离。

支持向量与边界

1. 支持向量机的类型

支持向量机有两种类型：

线性支持向量机
非线性支持向量机

线性与非线性可分问题

1.1 线性支持向量机

线性SVM适用于训练数据近似线性可分的情况，在这种情况下，存在一个超平面可以将不同类的样本完全划分开。

使用支持向量分类器 (SVC：support vector classifier) 查找使类之间的边距最大化的超平面，scikit-learn 的 LinearSVC实现了一个简单的 SVC。

下面基于鸢尾花数据集，在二维空间上对两组数据进行分类，然后绘制超平面：

# Load libraries  
from sklearn.svm import LinearSVC 
from sklearn import datasets 
from sklearn.preprocessing import StandardScaler 
import numpy as np  

# Load data with only two classes and two features 
iris = datasets.load_iris() 
features = iris.data[:100,:2] 
target = iris.target[:100]  

# Standardize features  
scaler = StandardScaler() 
features_standardized = scaler.fit_transform(features)  

# Create support vector classifier 
svc = LinearSVC(C=1.0)  

# Train model  
model = svc.fit(features_standardized, target)

# Plot data points and color using their class  
color = ["red" if c == 0 else "black" for c in target] 
plt.scatter(features_standardized[:,0], features_standardized[:,1], c=color)

# Create the hyperplane 
w = svc.coef_[0] 
a = -w[0] / w[1] 
xx = np.linspace(-2.5, 2.5) 
yy = a * xx - (svc.intercept_[0]) / w[1]

# Plot the hyperplane 
plt.plot(xx, yy) 
plt.xlabel('Sepal length [standardized]')
plt.ylabel('Sepal width [standardized]')
plt.tight_layout()
plt.legend()
plt.show()