摘选自:
软件设计师の备考经验帖及复习资料-Laptoy-优快云博客
软件设计师:数据结构与算法![]() https://blog.youkuaiyun.com/apple_53947466/article/details/125691927?fromshare=blogdetail&sharetype=blogdetail&sharerId=125691927&sharerefer=PC&sharesource=lapiii&sharefrom=from_link仅仅作为个人极限备考复习,去除完全不想看的真题,保留部分概念,目标是在最短时间内过完概念然后做题。
https://blog.youkuaiyun.com/apple_53947466/article/details/125691927?fromshare=blogdetail&sharetype=blogdetail&sharerId=125691927&sharerefer=PC&sharesource=lapiii&sharefrom=from_link仅仅作为个人极限备考复习,去除完全不想看的真题,保留部分概念,目标是在最短时间内过完概念然后做题。
数据结构
一、复杂度
1.1、大O表示法

1.2、时间复杂度

1.3、空间复杂度
二、渐进符号
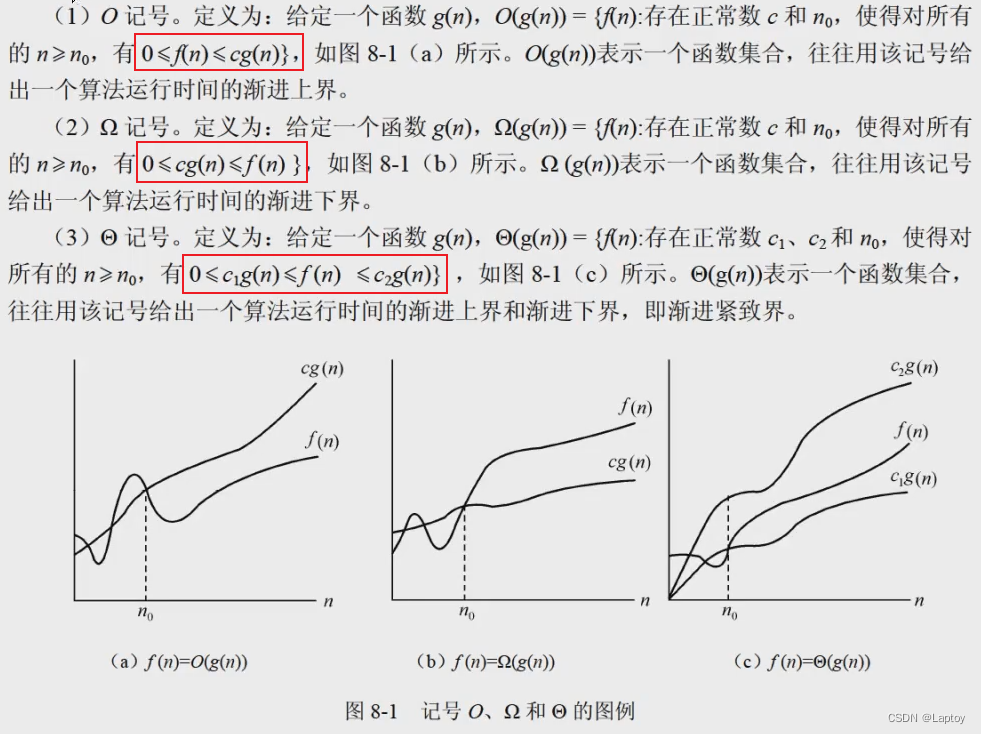
- 渐进上界:大于等于平均时间复杂度
- 渐进下界:小于等于平均时间复杂度
- 渐进紧致界:等于平均时间复杂度

若 f(n)=O(g(n)) 且 f(n)=Ω(g(n)),则称 f(n)=Θ(g(n))。
下面我们对每个等式逐一进行分析:
题目1 - 3是需要小于等于一个常数
(1) 判断 10n2+4n+2=O(n2) 是否成立
当 n≥1 时,有:
10n2+4n+2≤10n2+4n2+2n2=16n2
此时取 c=16,n0=1,满足大 O 表示法的定义,所以 10n2+4n+2=O(n2) 成立。
(2) 判断 10n2+4n+2=O(n3) 是否成立
当 n≥1 时,有:
10n2+4n+2≤10n3+4n3+2n3=16n3
此时取 c=16,n0=1,满足大 O 表示法的定义,所以 10n2+4n+2=O(n3) 成立。
(3) 判断 10n2+4n+2=O(n) 是否成立
假设存在正常数 c 和 n0,使得当 n≥n0 时,10n2+4n+2≤c⋅n。
即 10n+4+2n≤c,当 n 趋于无穷大时,10n+4+2n 也趋于无穷大,不可能小于等于一个常数 c,所以 10n2+4n+2=O(n) 不成立。
题目4-6 是需要大于等于一个正常数c
(4) 判断 10n2+4n+2=Ω(n2) 是否成立
当 n≥1 时,有:
10n2+4n+2≥10n2
此时取 c=10,n0=1,满足大 Ω 表示法的定义,所以 10n2+4n+2=Ω(n2) 成立。
(5) 判断 10n2+4n+2=Ω(n3) 是否成立
假设存在正常数 c 和 n0,使得当 n≥n0 时,10n2+4n+2≥c⋅n3。
即 10n+4n2+2n3≥c,当 n 趋于无穷大时,10n+4n2+2n3 趋于 0,不可能大于等于一个正常数 c,所以 10n2+4n+2=Ω(n3) 不成立。
(6) 判断 10n2+4n+2=Ω(n) 是否成立
当 n≥1 时,有:
10n2+4n+2≥10n
此时取 c=10,n0=1,满足大 Ω 表示法的定义,所以 10n2+4n+2=Ω(n) 成立。
7-9是要取一个等号
(7) 判断 10n2+4n+2=Θ(n2) 是否成立
由(1)可知 10n2+4n+2=O(n2),由(4)可知 10n2+4n+2=Ω(n2),根据大 Θ 表示法的定义,所以 10n2+4n+2=Θ(n2) 成立。
(8) 判断 10n2+4n+2=Θ(n3) 是否成立
由(2)可知 10n2+4n+2=O(n3),但由(5)可知 10n2+4n+2≠Ω(n3),不满足大 Θ 表示法的定义,所以 10n2+4n+2=Θ(n3) 不成立。
(9) 判断 10n2+4n+2=Θ(n) 是否成立
由(3)可知 10n2+4n+2≠O(n),由(6)可知 10n2+4n+2=Ω(n),不满足大 Θ 表示法的定义,所以 10n2+4n+2=Θ(n) 不成立。
三、递归
3.1、时空间复杂度
第一个函数
int f(int n)
{
if(n==1)
return 1;
return f(n - 1);
}- 时间复杂度分析:该函数是一个简单的递归函数,每次递归调用时,问题规模
n减 1,直到n等于 1 时递归结束。递归调用的次数与n的值成正比,因此时间复杂度为 O(n)。 - 空间复杂度分析:在递归调用过程中,每次调用都会在栈上分配一定的空间来保存函数的局部变量和返回地址。由于递归的深度为
n,所以空间复杂度为 O(n)。
第二个函数
c
int f(int n)
{
int i = 1;
if(n == 1)
return 1;
return f(n / 2);
}- 时间复杂度分析:每次递归调用时,问题规模
n变为原来的一半,即 n/2。设递归调用的次数为 k,则有 n/2k=1,解得 k=log2n。所以时间复杂度为 O(log2n)。 - 空间复杂度分析:递归的深度为 log2n,因此空间复杂度为 O(log2n)。
第三个函数
int f(int n)
{
int i = 1;
while (i <= n)
{
// 这里循环体为空,但不影响复杂度分析
}
return n * f(n - 1);
}- 解题引导:分析这个函数时,我们需要分别考虑循环部分和递归部分对时间复杂度和空间复杂度的影响。
- 时间复杂度分析:
-
- 循环部分
while (i <= n)的时间复杂度为 O(n)。 - 递归部分
return n * f(n - 1)每次递归调用时,问题规模n减 1,递归调用的次数为n次。 - 综合起来,时间复杂度为 O(n2)。
- 循环部分
- 空间复杂度分析:递归的深度为
n,所以空间复杂度为 O(n)。
若某算法在问题规模为n时,其基本操作的重复次数可由下式表示,则该算法的时间复杂度为(64)。
![]()
A.O(n)B.O(n2)C.O(logn)D.O (nlogn)
答案:B
解析:T(n)=T(n-1)+n=T(n-2)+n-1+n=……=T(1)+n+(n-1)+(n-2)+……+2=n(n+1)/2,时间复杂度为0(n2。)。
四、线性结构
4.1、定义
4.2、存储结构
4.3、顺序存储
插入和删除元素的代码和时间复杂度
- 最好的情况就是直接在顺序表后面插入一个元素,时间复杂度为O(1)
- 最坏的情况是在插入一个元素到原来第一个元素的位置,时间复杂度为O(n)
- 平均复杂度为O(n)
4.4、链式存储
插入节点的时间复杂度

五、栈
5.1、定义
5.2、真题
六、队列
6.1、定义
6.2、真题
6.3、栈与队列真题
七、串
7.1、定义
7.2、真题
7.3、串的模式匹配和朴素匹配
7.4、真题
八、数组

九、矩阵
9.1、对称矩阵

9.2、三对角矩阵
9.3、稀疏矩阵

十、树
10.1、定义
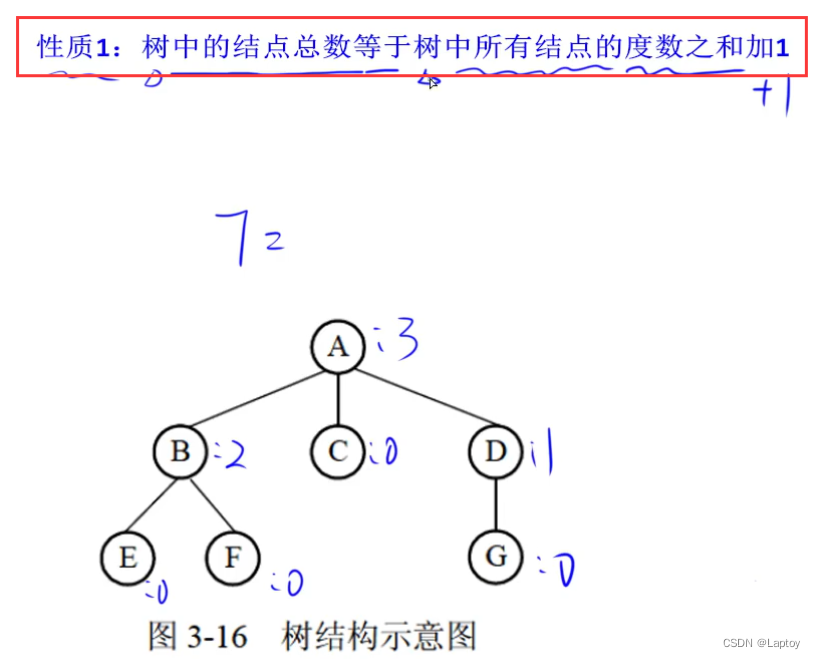
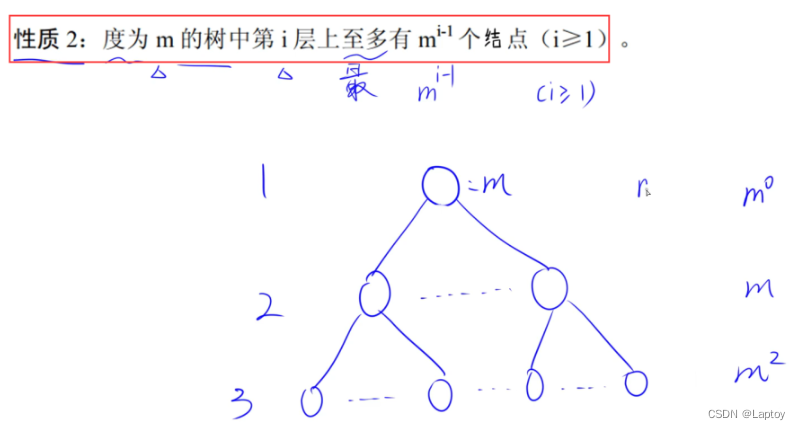
10.2、树的性质
十一、二叉树
11.1、定义

11.2、存储结构
11.2、真题
11.3、遍历
11.3、反向构造
11.3、真题
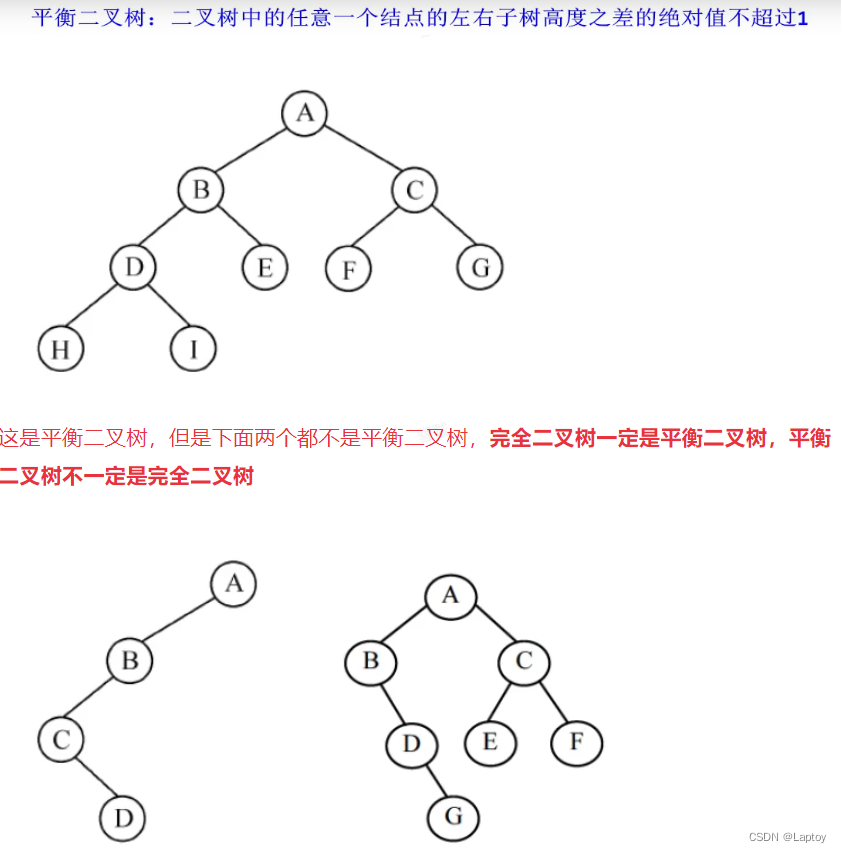
11.4、平衡二叉树
11.4、二叉排序树
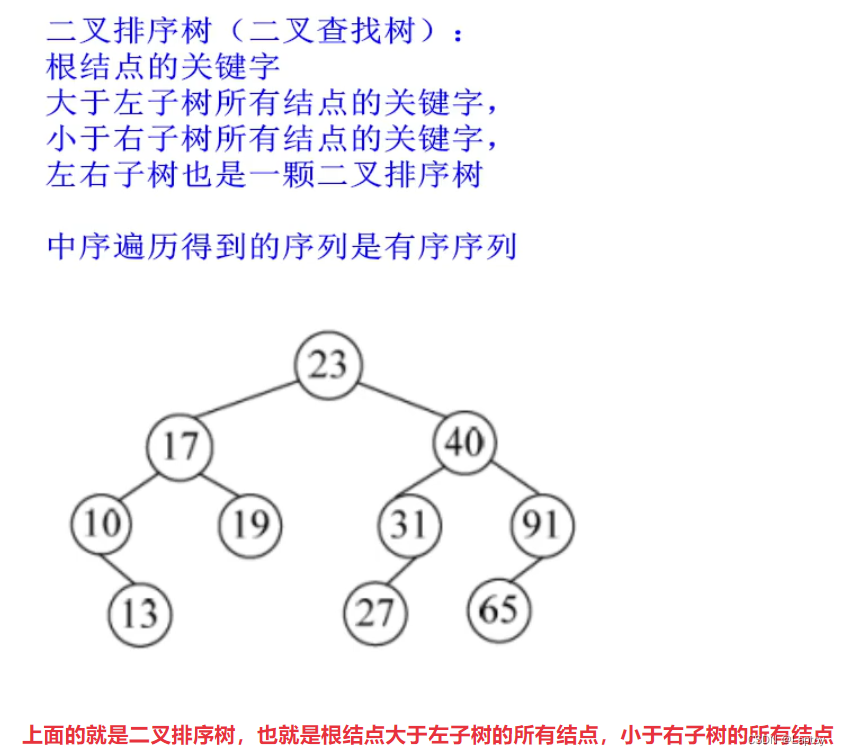
11.4、真题
11.5、最优二叉树(哈夫曼树)

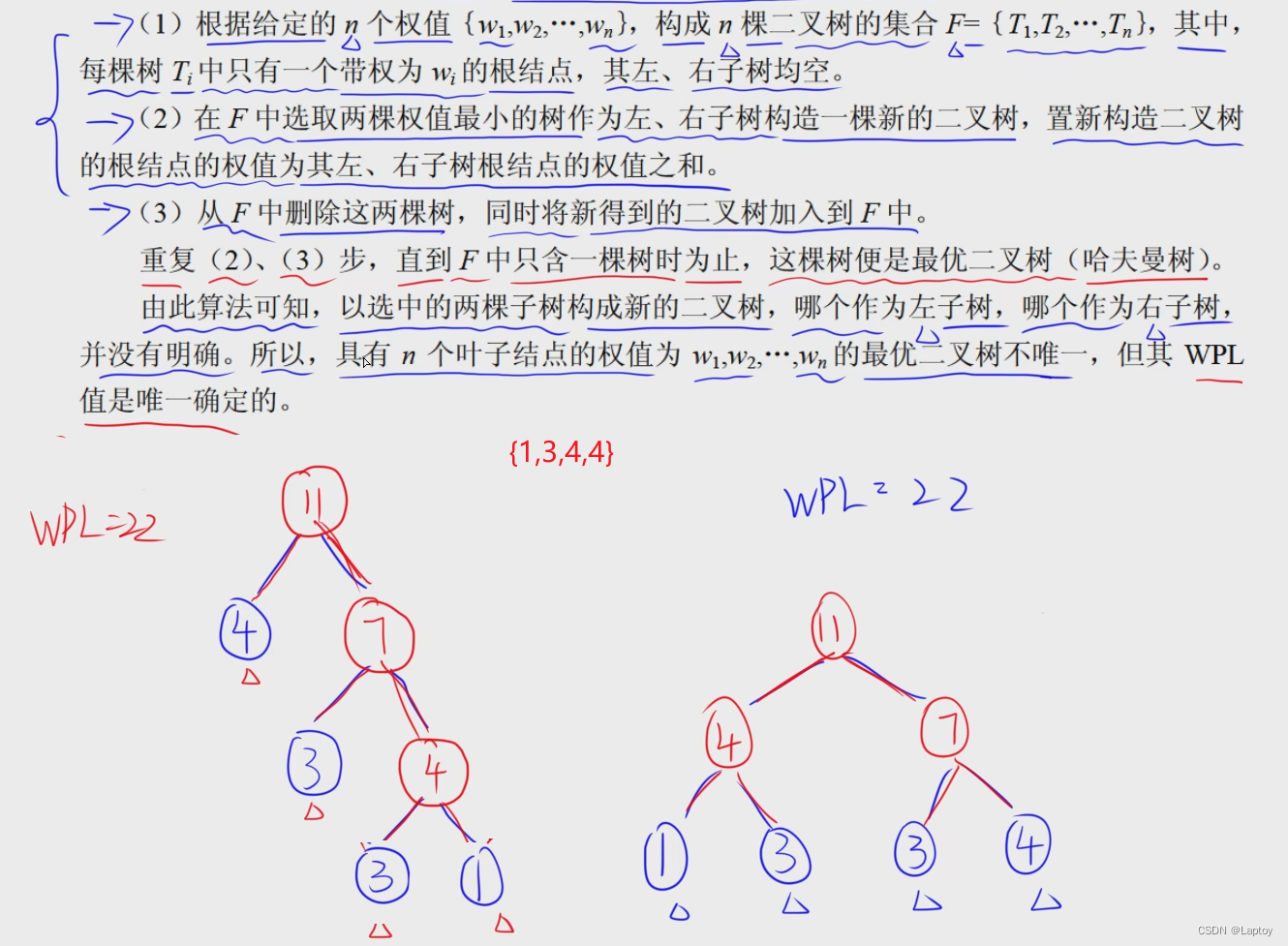
11.5、哈夫曼编码
11.5、哈夫曼编码压缩比
11.5、真题
11.6、线索二叉树
11.7、混合题
十二、图
12.1、定义
12.1、真题
12.2、邻接矩阵
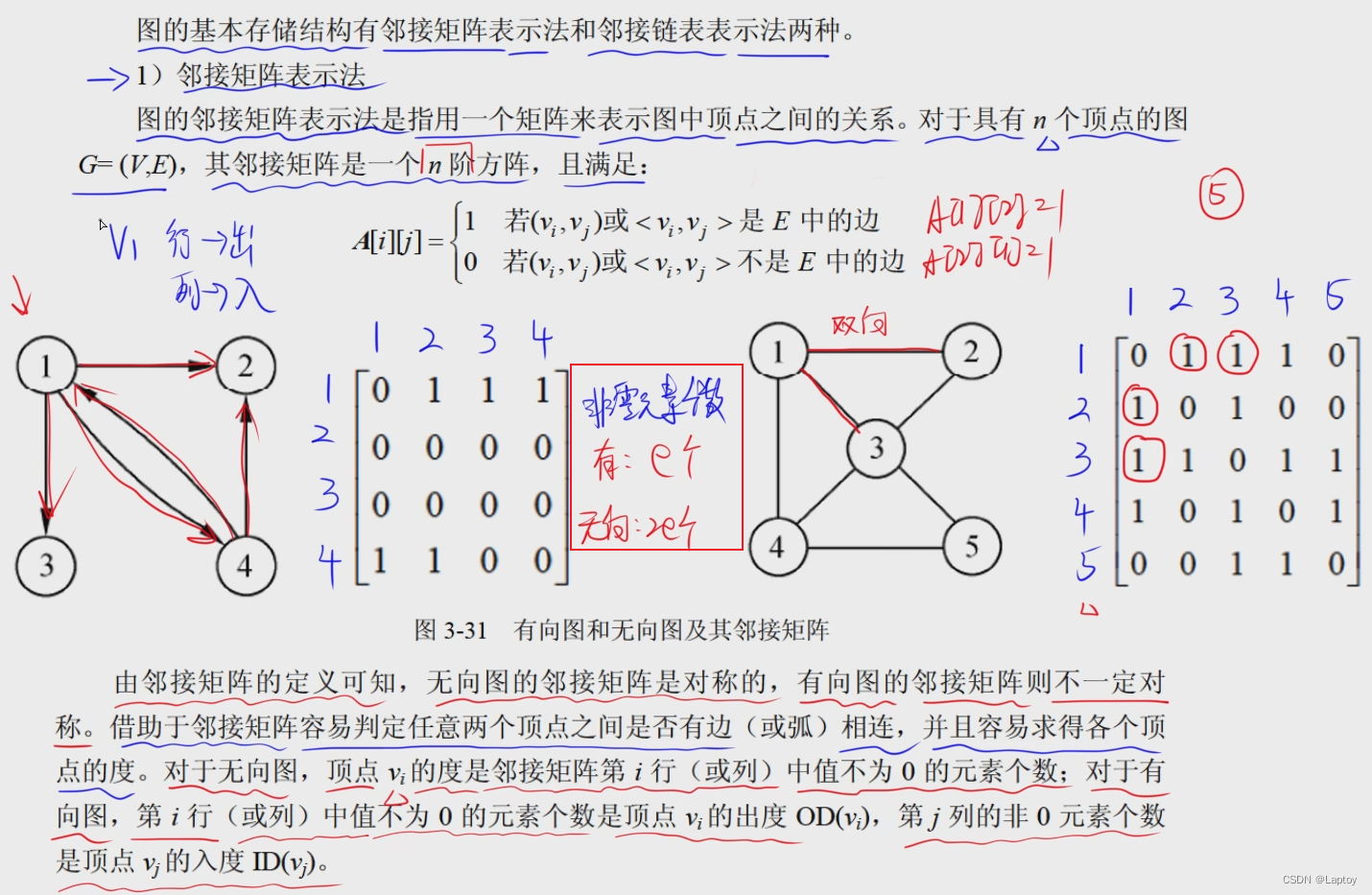
12.2、邻接表
12.2、稠密图和稀疏图
12.2、真题
12.3、图的遍历
12.4、拓扑排序

十三、查找
13.1、顺序查找
13.2、二分查找
13.3、真题
十四、哈希表
14.1、哈希表定义
14.2、哈希函数构造与处理冲突
14.3、处理冲突扩展
14.4、哈希表的查找
14.5、真题
十五、堆
15.1、定义
15.2、构造
15.3、真题
十六、排序
16.1、定义
1. 插入排序(稳定、不归位)
- 核心步骤:
从第2个元素开始,每次拿当前元素(未排序区首元素),往前遍历已排序区,把比它大的元素依次后移,空出位置后插入当前元素。 - 代码关键:
两层循环,外层控制未排序元素(i从1到n-1),内层从i-1往前找插入位置(j--),移动元素后插入temp。 - 特点:边插边调整,元素不会一下子到最终位置(不归位),相等元素不移动(稳定)。
2. 希尔排序(不稳定)
- 核心步骤:
先按“步长”(如n/2、n/4…直到1)把数组分成多个子数组,对每个子数组做插入排序;步长逐渐缩小到1,最后一次就是普通插入排序。 - 代码关键:
外层循环控制步长(gap从n/2递减到1),内层按步长对每个子数组执行插入排序(移动元素时步长为gap)。 - 特点:大步长先粗略排序,小步长微调,效率比插入排序高,但相同元素可能被分到不同子数组打乱顺序(不稳定)。
3. 选择排序(不稳定、归位)
- 核心步骤:
每次从剩余未排序元素中找最小的,和未排序区的第一个元素交换,这样最小元素就固定在最终位置(归位),重复到所有元素排完。 - 代码关键:
外层循环控制已排序区长度(i从0到n-2),内层循环找i之后的最小元素下标(minIdx),找到后和arr[i]交换。 - 特点:每次确定一个元素的最终位置(归位),但交换可能打乱相同元素顺序(如
[2,2,1]交换后两个2顺序变,不稳定)。
4. 堆排序(不稳定、归位)
- 核心步骤:
-
- 先把数组构建成“大根堆”(父元素≥子元素,堆顶是最大元素);
- 把堆顶(最大元素)和数组末尾元素交换(归位),再把剩余元素重新调整为大根堆;
- 重复步骤2,直到所有元素归位。
- 代码关键:
实现HeapAdjust函数(调整堆结构),先构建堆,再循环交换堆顶和末尾元素并调整堆。 - 特点:每次交换后末尾元素就是当前最大值(归位),堆调整时相同元素的位置交换可能破坏稳定性。
5. 冒泡排序(稳定、归位)
- 核心步骤:
从左到右两两比较相邻元素,若左边大则交换,让大元素像气泡一样“浮”到右侧;每轮结束后,最右侧的元素就是当前最大值(归位),重复到所有元素排完。 - 代码关键:
外层循环控制轮次(i从0到n-2),内层循环比较j和j+1(范围随i缩小,已归位元素不比较),相等时不交换(稳定)。 - 特点:每轮确定一个最大元素的最终位置(归位),相同元素不交换(稳定)。
6. 快速排序(不稳定、归位)
- 核心步骤:
-
- 选一个“基准值”(如首元素),通过划分把数组分成两部分:左边≤基准,右边≥基准,基准值固定在中间(归位);
- 对左右两部分分别递归执行步骤1,直到子数组长度为1。
- 代码关键:
实现Partition函数(划分逻辑:左右指针向中间移动,交换元素,最终基准归位),递归处理左右子数组。 - 特点:每次划分确定基准值的最终位置(归位),划分时交换可能打乱相同元素顺序(不稳定)。
7. 归并排序(稳定、不归位)
- 核心步骤:
-
- 递归把数组分成左右两半,直到子数组长度为1(天然有序);
- 合并两个有序子数组:用临时数组按顺序存放两部分元素(相等时取左边元素,保证稳定),再拷贝回原数组。
- 代码关键:
递归拆分(mid = (low+high)/2),实现Merge函数(合并两个有序数组到临时数组,再拷贝回去)。 - 特点:通过合并逐步有序,元素不会直接到最终位置(不归位),合并时保留相同元素顺序(稳定)。
这些算法的核心区别在于“如何移动元素”和“是否一次性确定元素的最终位置”,理解这两点就能快速掌握它们的实现逻辑~
程序设计
一、解释与编译
解释器:翻译时不生成独立的目标程序,解释程序和源程序都参与程序运行过程
编译器:翻译时独立生成目标程序,源程序和编译程序不再参与目标程序的运行过程
二、程序设计语言的成分

三、传值与传地址

四、编译、解释与翻译阶段
反编译:编译的逆过程,将可执行文件转换成等价的汇编程序(无法获得源程序)
源程序—》词法分析-》记号流–》语法分析–》分析树(语法树)–》语义分析

五、符号表

六、编译过程

七、正规式
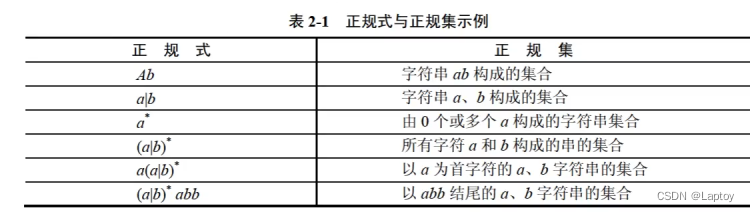
八、有限自动机
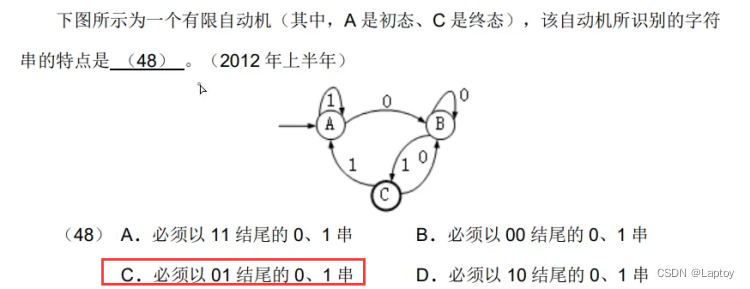
九、上下文无关文法

十、中缀后缀表达式
中缀表达式就是我们日常写的数学式子(如 3 + 4 × 2),后缀表达式则是把运算符放在两个操作数后面的式子(如 3 4 +)
 软考数据结构与程序设计核心考点
软考数据结构与程序设计核心考点





















 455
455

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








