洛谷P1172 安全逃离

最新推荐文章于 2025-02-05 17:22:58 发布
最新推荐文章于 2025-02-05 17:22:58 发布
阅读量685 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： 洛谷 文章标签： c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/lanyecch/article/details/105882399
本文介绍了洛谷P1172题目的详细解题思路，包括题目描述、输入输出格式，以及三种情况的枚举算法。通过定义结构体、安全函数，判断奶牛是否能安全逃离农场。文章提供了AC代码，帮助理解如何在给定的地图上寻找安全的逃离方案。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

洛谷P1172 安全逃离


101枚举NO:09

题面

P1172

难度：☆☆☆（普及/提高-）
知识点：01枚举，暴力；02模拟

题目描述

农夫john最近在研究如果发生重大事故，如何让农场里的奶牛逃离问题。他想要确信在紧急情况下，所有的奶牛都有一个安全逃离方案。因为在紧急情况下，奶牛们都会失去观察和判断能力，所以最近john一直在教奶牛们逃离的方法，他的方法很简单，就是任何时候都只向北方或东方逃离，北方是行坐标减1的方向，东方是列坐标加1的方向。奶牛们虽笨，不过这一点事关自己的生命，所以他们牢记在心，而且也一定会这么做。

当然也会出问题，奶牛们在逃离的方向上会横冲直撞，为了阻止奶牛之间互相冲撞造成伤害，john要求任何一个奶牛的逃离路线不能经过其它奶牛的初始位置。一个逃离方案是安全的如果它能够满足上面的要求，反之它就是不安全的。

奶牛们所在的土地（农场）被划分成了rr行和cc列的一个矩形地图。奶牛们都待在这个矩形中的某一个位置。

请帮助john确定给定的一个地图上是否存在一个安全的逃离方案。

比如，下面的两个图：

左边的例子表示了一个能够安全逃离的地图，因为没有任何一个奶牛的逃离路线上包括其他奶牛。右边的例子表示了一个不安全的地图，因为位于(4,1)(4,1)的奶牛不论是向东逃离还是向北逃离，它的路线上都会有别的奶牛，从这个图中拿掉任意一头奶牛，这个地图都会变成安全的。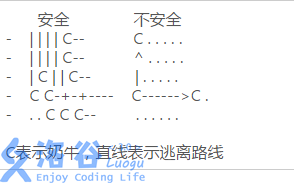在这里插入图片描述

输入格式

第1行：两个整数r,c，用1个空格隔开，表示矩形的行数和列数（均≤50）。

第2行：

最低0.47元/天 解锁文章

200万优质内容无限畅学
洛谷P1172 安全逃离题解
菜鸡Jacky0705的优快云博客
12-05 1630
洛谷【P1172】安全逃离题解题目 题目 农夫john最近在研究如果发生重大事故，如何让农场里的奶牛逃离问题。他想要确信在紧急情况下，所有的奶牛都有一个安全逃离方案。因为在紧急情况下，奶牛们都会失去观察和判断能力，所以最近john一直在教奶牛们逃离的方法，他的方法很简单，就是任何时候都只向北方或东方逃离，北方是行坐标减1的方向，东方是列坐标加1的方向。奶牛们虽笨，不过这一点事关自己的生命，所以他们...
P1172 安全逃离
weixin_44132485的博客
05-18 270
一、题目 二、解题思路 1.这道题是真的坑，题目描述是错的。有三处错误：（1）输入数据中存在除数字以外的无用字符串；（2）当删除一头牛可以变安全时，不需要输出1；（3）不是输出编号最小的牛，而是按序输出所有满足要求的奶牛。 2.看题目一定要认真，刚开始我把这道题想的复杂了，以为奶牛每次都可以向北或者向东，那样每头奶牛的路线很多，需要深搜，但实际上，这道题奶牛只有两条路线，一路向北或者向东。 3.问题的规模很小，用暴力也可以解决。这里提供一个非暴力的思路：首先查看所有的奶牛是否可以安全逃离，如果不能逃离的，
[洛谷]P1172 安全逃离 (#模拟)
A.pro的博客
07-25 1225
题目描述 农夫john最近在研究如果发生重大事故，如何让农场里的奶牛逃离问题。他想要确信在紧急情况下，所有的奶牛都有一个安全逃离方案。因为在紧急情况下，奶牛们都会失去观察和判断能力，所以最近john一直在教奶牛们逃离的方法，他的方法很简单，就是任何时候都只向北方或东方逃离，北方是行坐标减1的方向，东方是列坐标加1的方向。奶牛们虽笨，不过这一点事关自己的生命，所以他们牢记在心，而且也一定会这么做。...
洛谷P2638 安全系统
2302_79431881的博客
02-05 1607
这题纯组合数学，用高中学过的知识就能过。
洛谷 P1164 小A点菜讲解PPT
03-12
洛谷 P1164 小A点菜讲解PPT 本资源是关于洛谷 P1164 题目的讲解PPT，题目名称为小A点菜，通过对题目的分析和解决方法的讲解，帮助学习者更好地理解和掌握该题目的解决思路和方法。 知识点一：01背包问题 在本题目...
洛谷 P5660 [CSP-J2019] 数字游戏 C++代码
10-21
洛谷 P5660 [CSP-J2019] 数字游戏 C++代码 洛谷题目代码截图，如果要源代码的话私信我 有什么不懂的一定要问！！！不懂就问！！！ 我是一个小学生，没事喜欢写写代码，欢迎指出问题！
洛谷 P1172 安全逃离 题解
Lotuses的博客
08-25 493
数据点望 Luogu 能完善下 好，讲解正式开始。 拿到正确题目后，能想到的就是模拟、暴力。虽然这是一道普及的题目，我们也要将代码优化得更加 短小精干。 我们要模拟啥呢？ 1、首先，对于每一个牛，我们都要检查他能不能离开。 对于每一个牛，它上方格子或右方格子中，一定要有一条完全没有其他牛。 就说上文的样例。444 号上方有 111 号，向上走行不通。同时有房还有 666 号，向右走，也行不通。所以这头牛就不能安全逃出。 同样我们可以看出，要让整个图安全，只要去掉 111，444，666 的任意一个，就可以解
逃离
kaiyekai的专栏
04-19 928
看了下微薄, 盛大推出一款手机,百度推出一款手机,中兴..., 华为... 关于手机的消息好多啊.   迅速逃离这里领域, 竞争太激励了...逃离这个五代十国的战乱市场吧...
守望者的逃离贪心解法
10-23
守望者的逃离贪心解法,
安全逃离的题解
ZHK's blog
04-12 630
也农夫john最近在研究如果发生重大事故，如何让农场里的奶牛逃离问题。他想要确信在紧急情况下，所有的奶牛都有一个安全逃离方案。因为在紧急情况下，奶牛们都会失去观察和判断能力，所以最近john一直在教奶牛们逃离的方法，他的方法很简单，就是任何时候都只向北方或东方逃离，北方是行坐标减1的方向，东方是列坐标加1的方向。奶牛们虽笨，不过这一点事关自己的生命，所以他们牢记在心，而且也一定会这么做。 当然也...
暴力算法-BF（Brute Force）
To be a better man
03-13 9551
BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力算法。 该算法最坏情况下要进行M*(N-M+1)次比较，时间复杂度为O(M*N)。 时间复杂度太高，往往不推荐。 ...
【算法题】逃离农场
xiaxzhou的博客
06-17 2273
状态转移方程： 使用dp[i][j][t]表示前ii头奶牛中选取j头的和除以nn余为tt的方案数则方案分为两种：选取了第ii头奶牛和没有选取第ii头奶牛两个子问题 没有选择第ii头奶牛的方案数： dp[i−1][j][t]dp[i-1][j][t] 选择第ii头奶牛的方案数： dp[i−1][j−1][((t+n)−j)dp[i-1][j-1][((t+n)-j)%n] dp[
最近在研究的一个东东-移动证券
移动开发与培训
12-29 601
 Trackback: http://tb.blog.youkuaiyun.com/TrackBack.aspx?PostId=1650255
大逃离（洛谷 P2829）
不知所云的博客
10-09 285
大逃离 题目背景 zrz走进了一个奇葩的迷宫，他发现自己迷路了，想逃出来，他好不容易数完了所有的路，累的快晕了，只好叫你帮忙咯。 题目描述 这是一棵有n个节点的图，有m条双向边，每一条路有w个单位距离，zrz在1的位置，出口在n的位置，不过zrz脑子出了点bug，于是不想走最短的路，想走第2短的路，第2短路径允许与最短路径有重边，然后也可以重复通过一些节点和路，注意如果有多条路径都是最短路径，那么...
最近在研究swarm,郁闷
西涛offbye-移动全栈技术博客
05-30 1794
最近在研究swarm,郁闷有人用swarm做经济系统的仿真吗? 我们可以交流一下啊，最近遇到了很多问题。在linux FC3下有人安装成功了吗？？大家觉得这个研究方向有前途吗？？？？好像国内很少有人做，可能学经济的回编程的少吧！
洛谷p
最新发布
03-21
### 关于动态规划 (Dynamic Programming, DP) 的解决方案 在解决洛谷平台上的编程问题时，尤其是涉及动态规划的题目，可以采用以下方法来构建解决方案： #### 动态规划的核心思想 动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。其核心在于存储重复计算的结果以减少冗余运算。通常情况下，动态规划适用于具有重叠子问题和最优子结构性质的问题。 对于动态规划问题，常见的思路包括定义状态、转移方程以及边界条件的设计[^1]。 --- #### 题目分析与实现案例 ##### **P1421 小玉买文具** 此题是一个典型的简单模拟问题，可以通过循环结构轻松完成。以下是该问题的一个可能实现方式： ```cpp #include <iostream> using namespace std; int main() { int n; cin >> n; // 输入购买数量n double p, m, c; cin >> p >> m >> c; // 输入单价p，总金额m，优惠券c // 计算总价并判断是否满足条件 if ((double)n * p <= m && (double)(n - 1) * p >= c) { cout << "Yes"; } else { cout << "No"; } return 0; } ``` 上述代码实现了基本逻辑：先读取输入数据，再根据给定约束条件进行验证，并输出最终结果[^2]。 --- ##### **UOJ104 序列分割** 这是一道经典的区间动态规划问题。我们需要设计一个二维数组 `f[i][j]` 表示前 i 次操作后得到的最大价值，其中 j 是最后一次切割的位置。具体实现如下所示： ```cpp #include <bits/stdc++.h> using namespace std; const int MAXN = 5e3 + 5; long long f[MAXN], sumv[MAXN]; int a[MAXN]; int main(){ ios::sync_with_stdio(false); cin.tie(0); int n,k; cin>>n>>k; for(int i=1;i<=n;i++)cin>>a[i]; for(int i=1;i<=n;i++)sumv[i]=sumv[i-1]+a[i]; memset(f,-0x3f,sizeof(f)); f[0]=0; for(int t=1;t<=k;t++){ vector<long long> g(n+1,LLONG_MIN); for(int l=t;l<=n;l++)g[l]=max(g[l-1],f[t-1][l-1]); for(int r=t;r<=n;r++)f[r]=max(f[r],g[r]+sumv[r]*t); } cout<<f[n]<<'\n'; return 0; } ``` 这段程序利用了滚动数组优化空间复杂度，同时保持时间效率不变[^3]。 --- ##### **其他常见问题** 针对更复杂的路径覆盖类问题（如 PXXXX），我们往往需要结合一维或多维动态规划模型加以处理。例如，在某些场景下，我们可以设定 dp 数组记录到达某一点所需最小代价或者最大收益等指标[^4]。 --- ### 总结 以上展示了如何运用动态规划技巧去应对不同类型的算法挑战。无论是基础还是高级应用场合，合理选取合适的数据结构配合清晰的状态转换关系都是成功解决问题的关键所在。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值