聚类

1. K-Means(K均值)聚类

算法步骤：
(1) 首先我们选择一些类/组，并随机初始化它们各自的中心点。这需要提前预知类的数量(即中心点的数量)。
(2) 计算每个数据点到中心点的距离，数据点距离哪个中心点最近就划分到哪一类中。
(3) 计算每一类中中心点作为新的中心点。
(4) 重复以上步骤，直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点，然后选择运行结果最好的一个。
下图演示了K-Means进行分类的过程：

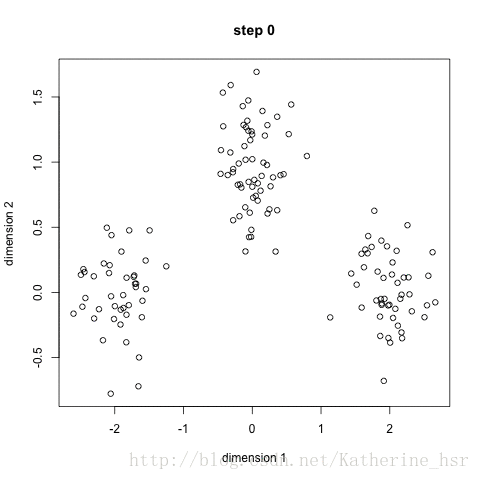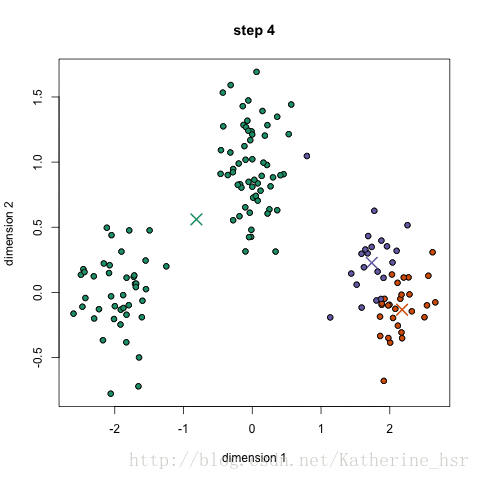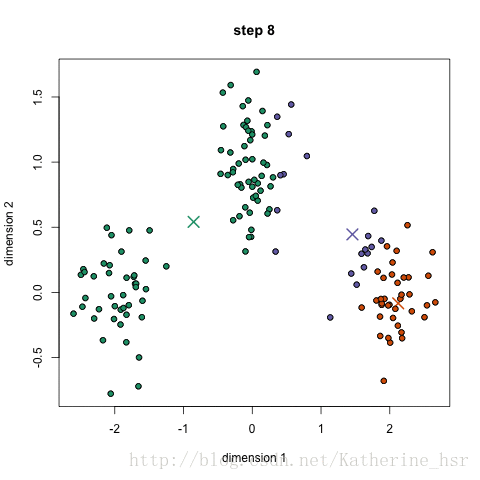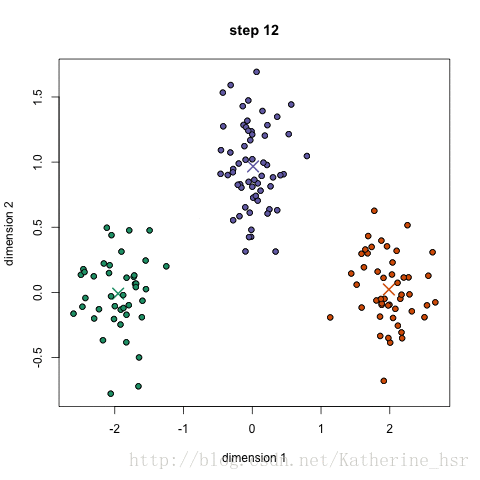
优点：
速度快，计算简便
缺点：
我们必须提前知道数据有多少类/组。

from sklearn.cluster import KMeans
'''
n_clusters：中心点的数量，默认8
max_iter：迭代次数，默认300
n_init：随机初始化的次数，默认10
'''
model = KMeans(n_clusters, max_iter, n_init)
model.labels_ #每个样本的类标记

2. 凝聚层次聚类

层次聚类算法分为两类：自上而下和自下而上。凝聚层级聚类(HAC)是自下而上的一种聚类算法。HAC首先将每个数据点视为一个单一的簇，然后计算所有簇之间的距离来合并簇，知道所有的簇聚合成为一个簇为止。
下图为凝聚层级聚类的一个实例：

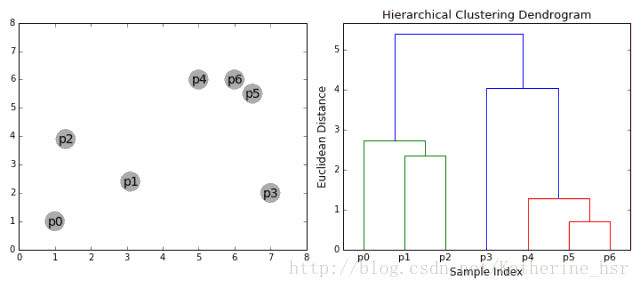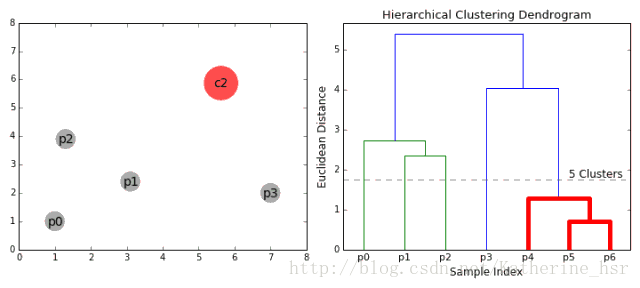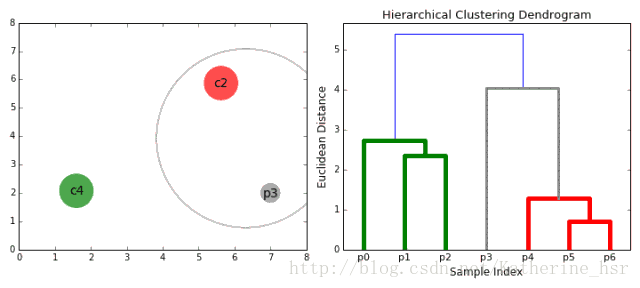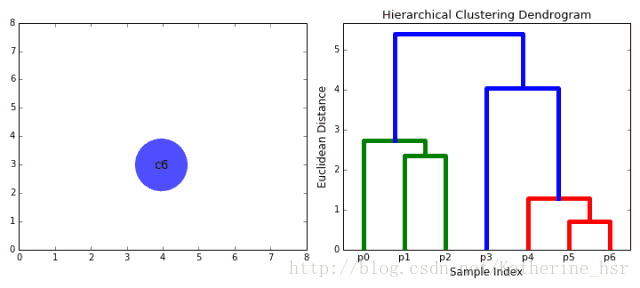
具体步骤：

1. 首先我们将每个数据点视为一个单一的簇，然后选择一个测量两个簇之间距离的度量标准。例如我们使用average linkage作为标准，它将两个簇之间的距离定义为第一个簇中的数据点与第二个簇中的数据点之间的平均距离。
2. 在每次迭代中，我们将两个具有最小average linkage的簇合并成为一个簇。
3. 重复步骤2知道所有的数据点合并成一个簇，然后选择我们需要多少个簇。

层次聚类优点：不需要知道有多少个簇
缺点：效率低

from sklearn.cluster import AgglomerativeClustering
'''
n_clusters：整数，需要分类簇的数量，默认2
linkage：字符串，用于指定链接算法，默认'ward'
		'ward'：单链接single-linkage，采用两个簇的样本对之间距离的最小值作为距离度量标准
		'complete'：全链接complete-linkage算法，采用两个簇的样本对之间距离的最大值作为距离度量标准
		'average'：均连接average-linkage算法，采用两个簇的样本对之间距离的平均值作为距离度量标准
'''
model = AgglomerativeClustering(n_clusters, linkage)

model.labels_ #每个样本的簇标记

3. 基于密度的聚类方法(DBSCAN)

具体步骤：

1. 首先确定半径r和minPoints. 从一个没有被访问过的任意数据点开始，以这个点为中心，r为半径的圆内包含的点的数量是否大于或等于minPoints，如果大于或等于minPoints则改点被标记为central point,反之则会被标记为noise point。
2. 重复1的步骤，如果一个noise point存在于某个central point为半径的圆内，则这个点被标记为边缘点，反之仍为noise point。重复步骤1，直到所有的点都被访问过。

优点：不需要知道簇的数量
缺点：需要确定距离r和minPoints

from sklearn.cluster import DBSCAN
'''
eps：半径r，默认0.5
min_samples：minPoints，默认5
'''
model = DBSCAN(eps, min_samples)

model.labels_ #聚类标签, 噪声样本标签为-1

4. 用高斯混合模型（GMM）的最大期望（EM）聚类

使用高斯混合模型（GMM）做聚类首先假设数据点是呈高斯分布的，相对应K-Means假设数据点是圆形的，高斯分布（椭圆形）给出了更多的可能性。我们有两个参数来描述簇的形状：均值和标准差。所以这些簇可以采取任何形状的椭圆形，因为在x，y方向上都有标准差。因此，每个高斯分布被分配给单个簇。

所以要做聚类首先应该找到数据集的均值和标准差，我们将采用一个叫做最大期望(EM)的优化算法。下图演示了使用GMMs进行最大期望的聚类过程。

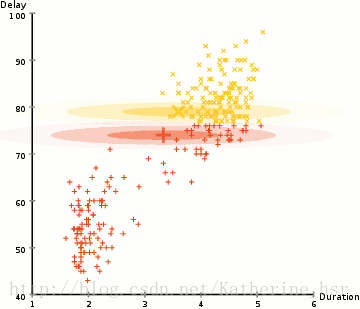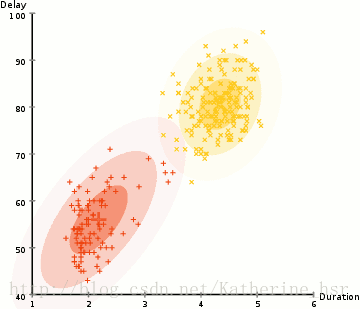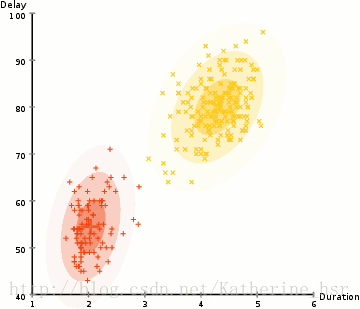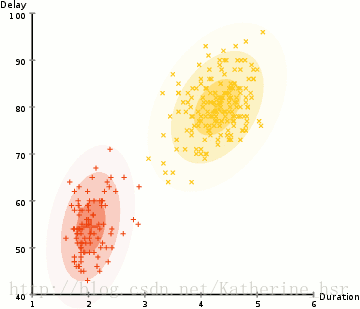
具体步骤：

1. 选择簇的数量（与K-Means类似）并随机初始化每个簇的高斯分布参数（均值和方差）。也可以根据先对数据用K均值进行分类后的结果给出一个相对精确的均值和方差。
2. 给定每个簇的高斯分布，计算每个数据点属于每个簇的概率。一个点越靠近高斯分布的中心就越可能属于该簇。
3. 基于这些概率我们计算高斯分布参数使得数据点的概率最大化，可以使用数据点概率的加权来计算这些新的参数，权重就是数据点属于该簇的概率。
4. 重复迭代2和3直到在迭代中的变化不大。

优点：

• 一个数据点可以属于多个簇。例如数据点X可以有百分之20的概率属于A簇，百分之80的概率属于B簇。也就是说GMMs可以支持混合。
• 聚类的外观具有灵活性。

缺点：

• GMM聚类对初始化值很敏感
• 可能收敛到局部最优
• 收敛速度慢

from sklearn.mixture import GaussianMixture
'''
n_components：混合高斯模型个数，默认1
covariance_type：协方差类型，包括{'full', 'tied', 'diag', 'spherical'}四种，默认'full'
                 'full': 分别对应完全协方差矩阵（元素都不为零）
                 'tied': 相同的完全协方差矩阵（HMM会用到）
                 'diag': 对角协方差矩阵（非对角为零，对角不为零）
                 'spherical': 球面协方差矩阵（非对角为零，对角完全相同，球面特性）
tol：EM迭代停止阈值，默认1e-3
n_init: 初始化次数，用于产生最佳初始参数，默认1 
'''
model = GaussianMixture(n_components, covariance_type, tol, n_init)

5. 聚类结果的评价（聚类验证）

轮廓系数(silhouette coefficient) 结合了凝聚度和分离度，其计算步骤如下：

1. 计算第 i 个对象到所属簇中所有其他对象的平均距离，记作a_i （体现凝聚度）
2. 计算第 i 个对象到距离它所属簇的最近簇中所有对象的平均距离，记 作b_i（体现分离度）
3. 第 i 个对象的轮廓系数为 $S_i=\frac{b_i-a_i}{max(a_i,b_i)}$
4. 所有对象轮廓系数的平均值就是整体的轮廓系数

轮廓系数取值为[-1, 1]，其值越大越好，且当值为负时，表明样本被分配到错误的簇中，聚类结果不可接受。对于接近0的结果，则表明聚类结果有重叠的情况。轮廓系数不适用于对DBSCAN模型作评价。

from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans

kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
#'euclidean'表示距离采用的是欧式距离
evaluation = silhouette_score(X, labels, metric='euclidean')

6. 聚类分析过程

数据 ——> 特征提取及选择 ——> 聚类算法的选择和微调 ——> 聚类验证 ——> 结果解析 ——> 信息