感知机算法

什么是感知机「Perceptron」

PLA全称是Perceptron Linear Algorithm，即线性感知机算法，属于一种最简单的感知机（Perceptron）模型。

感知机模型是机器学习二分类问题中的一个非常简单的模型。它的基本结构如下图所示：

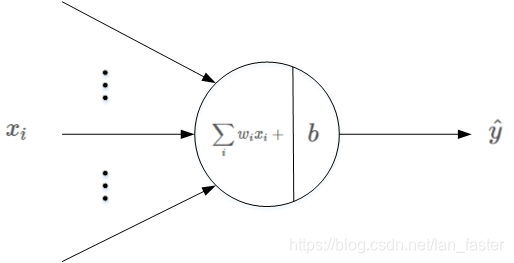
其中，xi是输入，wi表示权重系数，b表示偏移常数。感知机的线性输出为:

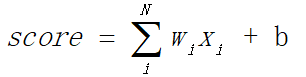
为了简化计算，通常我们将b作为权重系数的一个维度，即w0。同时，将输入x扩展一个维度，为1。这样，上式简化为：

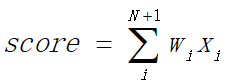
score是感知机的输出，接下来就要对score进行判断：

• 若scores≥0，则 $\hat{y}$ = 1（正类）
• 若scores<0，则 $\hat{y}$ = 0（负类）

以上就是线性感知机模型的基本概念，简单来说，它由线性得分计算和阈值比较两个过程组成，最后根据比较结果判断样本属于正类还是负类。

感知机算法

感知器步骤如下所示。以二维散点分类为例，对于坐标轴为(p,q)的点，标签 y，以及等式
$\hat{y}$ = step(w₁x₁ +w₂x₂+ b)给出的预测结果

• 如果点分类正确，则什么也不做。
• 如果点分类为正，但是标签为负，则更新参数为
  w₁ = w₁ - p*$\alpha$
  w₂ = w₂ - q*$\alpha$
  b = b - $\alpha$
• 如果点分类为负，但是标签为正，则更新参数为
  w₁ = w₁ + p*$\alpha$
  w₂ = w₂ + q*$\alpha$
  b = b + $\alpha$

注：$\alpha$为学习率，分类错误的情况下，标签为正就加，标签为负就减

示例代码

import numpy as np
# 设置随机数种子
np.random.seed(42)

def stepFunction(t):
    if t >= 0:
        return 1
    return 0

def prediction(X, W, b):
    return stepFunction((np.matmul(X,W)+b)[0])

# 更新参数
def perceptronStep(X, y, W, b, learn_rate = 0.01):
    for i in range(len(X)):
        y_hat = prediction(X[i],W,b)
        # y[i]=1, y_hat=0, 即标签为正，分类为负
        if y[i]-y_hat == 1:
            W[0] += X[i][0]*learn_rate
            W[1] += X[i][1]*learn_rate
            b += learn_rate
        # y[i]=0, y_hat=1, 即标签为负，分类为正
        elif y[i]-y_hat == -1:
            W[0] -= X[i][0]*learn_rate
            W[1] -= X[i][1]*learn_rate
            b -= learn_rate
    return W, b
    
# 感知机算法
def trainPerceptronAlgorithm(X, y, learn_rate = 0.01, num_epochs = 25):
	#初始化参数
    W = np.array(np.random.rand(2,1))
    b = np.random.rand(1)[0]
    
    #训练num_epochs轮，每轮执行perceptronStep
    for i in range(num_epochs):
        W, b = perceptronStep(X, y, W, b, learn_rate)
    return W, b