C++力扣每日一题-多米诺和托米诺平铺

最新推荐文章于 2025-12-18 16:28:22 发布

原创最新推荐文章于 2025-12-18 16:28:22 发布 · 407 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #leetcode #算法

该博客讨论了一种使用动态规划方法解决如何用2x1的多米诺形和形如'L'的托米诺形瓷砖平铺2xn面板的问题。通过观察n取小值时的结果，得出递推公式：res[n]=2*res[n-1]+res[n-3]，并给出C++代码实现，计算结果对10^9+7取模。

题目：
有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。
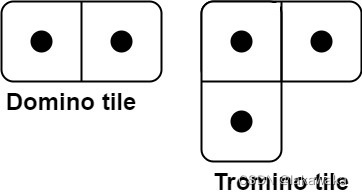
请添加图片描述
给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

思路：
列出n取1，2，3，4，5，6，7的值进行比较（有个小技巧，对于前面这些正确的返回值直接利用力扣的控制台输入对应的n，直接看“预期结果”即可，不用自己一个一个推），不难发现当n > 3 的时候，res[n] = 2 * res[n - 1] + res[n - 3], 那么思路就很明显了，直接从前到后递推上去就能找到答案。

代码：


class Solution {
public:
    int numTilings(int n) {
        vector<long long> dp(1001);
        dp[1] = 1, dp[2] = 2, dp[3] = 5;
        for(int i = 4; i <= n; i++){
            dp[i] = ((2 * dp[i - 1]) % moder  + dp[i - 3]) % moder;
        }
        return dp[n];
    }
private:
    int moder = 1000000007;
};