【动态规划】最长上升子序列模型——进阶

最新推荐文章于 2024-03-25 08:16:59 发布

原创

最新推荐文章于 2024-03-25 08:16:59 发布 · 561 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #acm竞赛

本文探讨了导弹防御系统中拦截策略，涉及最长非严格递减子序列的计算，以及如何通过贪心算法优化拦截导弹数量。同时，文章介绍了最长公共上升子序列问题，利用动态规划结合LIS和LCS的思想求解。

最长上升子序列模型

拦截导弹
导弹防御系统
最长公共上升子序列

拦截导弹

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。

但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

某天，雷达捕捉到敌国的导弹来袭。

由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式
共一行，输入导弹依次飞来的高度。

输出格式
第一行包含一个整数，表示最多能拦截的导弹数。

第二行包含一个整数，表示要拦截所有导弹最少要配备的系统数。

数据范围
雷达给出的高度数据是不大于 $30000$ 的正整数，导弹数不超过 $1000$ 。

输入样例：

389 207 155 300 299 170 158 65

输出样例：

6
2

分析： 这个题有两个小问，第一是问最多能拦截多少导弹，而我们一次能够拦截的导弹要求是后一发不能高于前一发，也就是说要求一个最长非严格递减子序列。
第二问拦截所有导弹最少要配备多少套这种导弹拦截系统，也就是求最少有多少个最长非严格递减子序列。这一问我们要使用贪心的策略。
策略如下:
从前往后扫每一个数，对于每个数
1.如果现在的所有子序列的结尾都小于当前的数（也就是说当前的导弹无法被现有的任何拦截系统拦截），则创建新的子序列
2.将当前数放在结尾大于等于它的最小的子序列的后面，这样我们就让所有序列剩下的能够放的数字尽可能的多
这样的贪心策略是最优的，简单证明一下。
如何证明两个数相等？
$A > = B, B > = A = > A = B$
$A$ ：贪心所得到的序列的个数
$B$ ：最优解（最少的序列个数）
$A > = B$ 是显然成立的，因为B是最优解
证明： $B > = A$ ：（调整法）
假设最优解对应的方案和当前方案不同。
找到第一个不同的数。
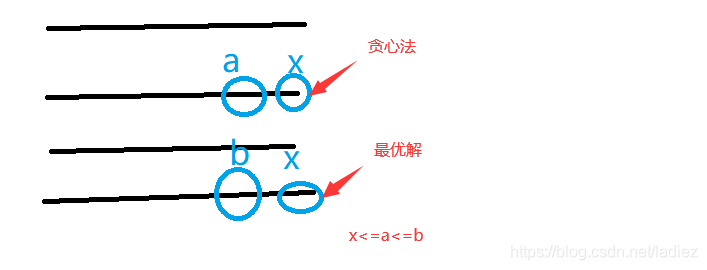
在这里插入图片描述
假设我们贪心法的x和最优解的x放在了上图的位置，那么有x<=a<=b，我们显然可以将a后面的一段和b后面的一段交换位置，这样是不会影响最后的最优解的。所以我们经过很多次的变化，我们没有增加子序列的个数，可以将贪心法变换到最优解的情况。所以得到A>=B。所以我们就可以按照这样的贪心策略来求最优解。
实际上这有一个Dilworth定理，可以自行搜索。
实现方法：我们维护一个数组ans，存储每一个序列的最后一个值，每一次增加一个数，如果当前数比ans中的所有数都大，也就是说当前的导弹无法被现有的任何拦截系统拦截，那么我们就要新开一个序列来存这个值。
否则，找到ans中比当前数大的数的最小值，替换ans数组中的这个值为当前数。
不难看出，ans数组是一个单调递增序列，可以使用二分来简化时间复杂度。
而这样的贪心策略和我们的最长递增子序列的贪心求解法 $O (n l o g n)$ 是一样的。所以第二问可以转化为求一个严格最长递增子序列。

代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int ans[1005],n,a[1005],k;
int main()
{
   
   
    while(~scanf("%d",&a[++n]));
    n--;
    for(int i=1;i<=n;i++){
   
   
        int id=upper_bound(ans,ans+k,a[i],greater<int>())-ans;
        if(id<k)ans[id]=a[i];
        else ans[k++]=a[i];
    }
    printf("%d\n",k);
    k=0;
    for(int i=1;i<=n;i++){
   
   
        int id=lower_bound(ans,ans+k,a[i])-ans;
        if(id<k)ans[id]=a[i];
        else ans[k++]=a[i];
    }
    printf("%d\n",k);
    return 0;
}