动态规划

最新推荐文章于 2025-07-25 20:07:40 发布

l_s_2020

最新推荐文章于 2025-07-25 20:07:40 发布

阅读量758

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构文章标签：数据结构

本文链接：https://blog.youkuaiyun.com/l_s_2020/article/details/106558372

数据结构专栏收录该内容

5 篇文章

订阅专栏

动态规划总结

最长上升子序列及其延伸
- LIS问题（LeetCode 300）
- 俄罗斯套娃信封问题（354）

最长上升子序列及其延伸

LIS问题（LeetCode 300）

题目描述：
最长上升子序列
1. DP的方法

定义状态
由于一个子序列一定会以一个数结尾，于是将状态定义成：dp[i] 表示以 nums[i] 结尾的「上升子序列」的长度。注意：这个定义中 nums[i] 必须被选取，且必须是这个子序列的最后一个元素。
状态转移方程
遍历到nums[i]时，需要把下标i之前的所有的数都要看一遍；只要nums[i]严格大于在它位置之前的某个数，那么nums[i]就可以接在这个数后面形成一个更长的上升子序列；因此，dp[i]就等于下标i之前严格小于**nums[i]**状态值的最大者+1.
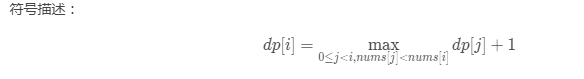
初始化
dp[i]=1, 1个字符显然是长度为1的上升子序列。
考虑输出
这里要注意，不能返回dp[i]的最后一个状态值，因为最后一个状态值只是nums[len-1]结尾的上升子序列的长度。
所有状态的最大值才是最后要输出的值

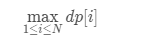
代码实现：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
      if(nums.size()<=1)
          return nums.size();
      int len=nums.size();
      vector<int> dp(len,1);
      int res=0;
      for(int i=1;i<len;i++){
          for(int j=0;j<i;j++){
              if(nums[j]<nums[i]) 
                 dp[i]=max(dp[i],dp[j]+1);
          }
          res=max(res,dp[i]);
      }
      return res;
    }
};

2. 动规+二分查找

俄罗斯套娃信封问题（354）

题目描述：
俄罗斯套娃信封问题
分析：此题是排序+最长上升子序列问题的组合。在对信封按w进行排序后，我们可以找到h上最长递增子序列的长度。考虑[[1，3]，[1，4]，[1，5]，[2，3]]，如果我们直接对 h 进行 LIS 算法，我们将会得到 [3，4，5]，显然这是错的，因为 w 相同的信封是不能够套娃的。为了解决这个问题。我们可以按** w** 进行升序排序，若 w 相同则按 h 降序排序。则上述输入排序后为 [[1，5]，[1，4]，[1，3]，[2，3]]，再对** h** 进行 LIS 算法可以得到 [5]，长度为 1，是正确的答案。

 1. C++中sort函数中的比较函数
 bool compare(T& a,T& b)
{
      return a<b;  //升序
      return a>b;  //降序
}
[sort比较函数的三种写法](https://blog.csdn.net/hzyong_c/article/details/7791415)
2.  Lambda 表达式用法(C++11)
[Lambda讲解](https://www.jianshu.com/p/a200a2dab960)

代码实现：

class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
       if(envelopes.size()==0)
           return 0;
        sort(envelopes.begin(),envelopes.end(),[](const vector<int>& a,const vector<int>& b){
            return a[0]<b[0]||(a[0]==b[0]&&a[1]>b[1]);
        });
        int n=envelopes.size();
        vector<int> dp(n,1);
        int res=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++)
              if(envelopes[i][1]>envelopes[j][1])
                 dp[i]=max(dp[j]+1,dp[i]);
            res=max(res,dp[i]);
        }
        return res;
    }
};

有关sort比较函数的进一步拓展

如果comp返回true，则第一个参数小于第二个参数，sort根据compare的返回值将第一个参数排在第二个参数之前；如果comp返回false，则第一个参数大于第二个参数，sort根据compare的返回值将第一个参数排在第二个参数之后。

题目描述
输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。（剑指offer）

思路：自定义比较器，若a+b>b+a则a>b，即”3”+”23”>”23”+”3”则3>23，并且我们希望在排序的时候将23排在3的前面，也就是升序排列。
代码实现：

class Solution {
public:
    static bool compare(const string& s1, const string& s2)
    {
        string ab = s1 + s2;
        string ba = s2 + s1;
        return ab < ba; //升序排列。如改为ab > ba, 则为降序排列
    }
    string PrintMinNumber(vector<int> numbers) 
    {
        string result;
        if(numbers.size() <= 0) return result;
        vector<string> num2str;
        for(int i = 0; i < numbers.size(); i++)
        {
            stringstream ss;
            ss << numbers[i];
            string s = ss.str();
            num2str.push_back(s);
        }
        sort(num2str.begin(), num2str.end(), compare);
        for(int i = 0; i < num2str.size(); i++)
        {
            result.append(num2str[i]);
        }
        return result;
    }
};

总结起来就是：
sort函数根据comp函数的返回值，对comp函数的两个参数排序。
如果comp返回true，排序为“参数1”“参数2”，否则排序为“参数2”“参数1”。
想要升序排列，则return parameter1<parameter2
想要降序排列，则return parameter1>parameter2