Machine Learning入门笔记(二) 模型评估与选择 (2)

2.3 性能度量

  前文已学习了如何划分Data set 以进行训练学习并测试，但光光这样是不够的，我们还需要确切可计算的参数来对一个模型，训练成果进行评估。this is performance measure.

2.3.0 均方误差

  均方误差(mean squared error)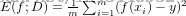     

  在回归任务中，这是一种最为常用的度量。训练目标是企图使均方误差最小化。(它象征着点与点之间的距离 是二次项)

  而这种使均方误差最小化 来建立模型的方法被称为 最小二乘法(least square method)

后文介绍分类任务的衡量指标。

2.3.1 错误率与精度

  分类错误数 占样本总数的比例。 ACC=1-E  

  错误率定义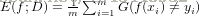：   G(k)为指示函数 if k: k=1  else: k=0

  更一般的，对于数据分布D和概密函数p(·) 错误率定义为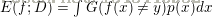  

2.3.2 查准、查全与F1 

  很多时候 仅仅知道多少分错了这一信息是不够用的。以挑西瓜为例 更仔细的 我们想知道被挑出来的好瓜，有多少个是真正的好瓜？有多少坏瓜没被挑出来？

  针对个体样本，设现实情况为 真true/假false;  而预测结果为 positive正例/negative反例

  这样划分 我们得到了如下  二分类混淆矩阵

  查准率(precision)的定义为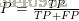： 所有pick出的正例中，选出真的比例

  查全率(recall)的定义为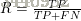：  全体真样本中，有多少被当做正例选出来了？

  P、R是一对矛盾的度量。比如希望提高R: 希望挑出所有好瓜-->放宽好瓜约束-->的确选出很多好瓜,但也会pick出坏瓜-->P降低。反之亦然。。同时提高P、R仅仅可能出现在某些十分简单的case中

  以R为x，P为y轴 可画出P-R图。若学习器A的P-R曲线完全包住学习器B的曲线，则表示A是性能更优越的学习器

  但是 每次通过积分计算P-R曲线的所围面积并不方便。人们因此引入其他度量。

  平衡点(Break-Even Point): 在P-R图取P=R(x=y)，与学习器的学习曲线的交点，即为平衡点 BEP大则学习能力强

  更常用的为度量F1：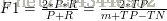

  应用中，P、R重要度往往不同，引入系数β( β>0)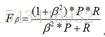 

  β<1 查准率P更重要; β=1退化成标准F1； β>1查全率R更重要

  当我们重复进行多次训练时，会得出多个二分类矩阵，那怎么确定该P、R呢？

  针对每个矩阵求出各自P、R 再求均值，此法为宏 得到macro-P、macro-R、macro-F1

  而针对所有矩阵的TP、TN、FP、FN 先求出这四个指标的均值得均值矩阵 再以此求出P、R此法为微 得micro-P、R

2.3.3 ROC与AUC

  存在很多学习器 学习并预测值h 将之与阈值th比较。 h>th 归正类；h<th 归反类。这个预测值h的好坏 就决定了泛化性能的好坏。我们将测试样本排序： 最可能是正例的排前列，最不可能是正例的排最后。 以此，从中选一个截断点，之前为正类，之后为反类。ROC曲线是以这种角度出发的研究有力工具。

  ROC(Receiver Operating Characteristic)全称是“受试者工作特征”曲线。

  真正例率(True Positive Rate): 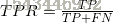   (所以成功预测的case中，包含多少正例？)

  假正例率(False Positive Rate): 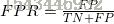  (所有预测失败的case中， 包含多少本假作真？)

  以FPR为横，TPR为纵轴，生成ROC曲线。ROC曲线下围面积被记作AUC(Area Under ROC Curve)

  通过比较AUC大小来衡量学习性能

2.3.4 代价敏感错误率和代价曲线

 unequal cost: FP、FN 两部分同为学习器的犯错，但其权重明显不同(人没病判成有病会吃无用的要，而病人未被诊断出病则危及性命)  因此更新一下二分类矩阵,设置FN(假反例)权重为cost_01, FP(假正例)权重为cost_10

  在这种非均等代价的情况下，我们希望总体代价越小越好。

  以正例概率代价为横轴，归一化代价 取值[0,1] 为纵轴 生成代价曲线，p为样例正例概率

  正例概率代价： 

  归一化代价：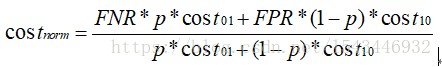

ROC曲线上每一个点对应代价平面上的一条线段，各线段和横轴围城的面积，即为期望总体代价