本文介绍了神经网络的基础知识，包括M-P神经元模型和常用的Sigmoid激活函数。讨论了感知机及其学习规则，并指出其在非线性问题上的局限性，进而引出多层前馈神经网络。重点讲解了误差逆传播（BP）算法，展示了其在网络参数更新中的应用。此外，还提到了防止过拟合的策略，如早停和正则化，并讨论了全局最小和局部最小的问题及应对方法。最后，简要提及了其他类型的神经网络，如RBF、ART和SOM网络。
神经网络——西瓜书笔记
-
神经元模型
神经网络中最基本的成分是神经模型，即“简单”单元。现在一直沿用的是“M-P神经元模型“，在这个模型中， 神经元接收到来自nnn个其他神经元传递过来的输入信号， 这些输入信号通过带权重的连接进行传递， 神经元接收到的中输入值与神经元的阈值进行比较，然后通过激活函数处理产生神经元的输出。
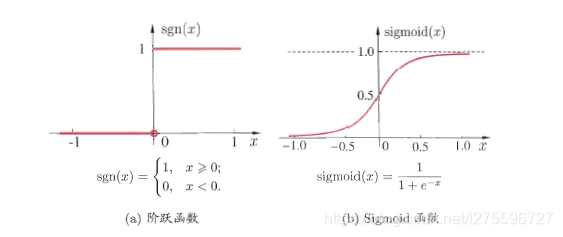
理想的激活函数是 阶跃函数， 但是由于阶跃函数 不连续、不光滑的性质， 因此实际常用 Sigmoid 函数作为 激活 函数。
-
感知机和多层网络
感知机由两层神经元组成， 输入层接收外界信号后传递给输出层， 输出层是 M-P神经元， 也称“阈值逻辑单元”。
感知机容易地实现逻辑与、或、非运算。注意到y=f(∑iwixi−θ)y=f(\sum_i w_ix_i -\theta)y=f(∑iwixi−θ),假设fff是上图中的阶跃函数，有：
- ”与“：令w1=w2=1,θ=2w_1= w_2 = 1 , \theta=2w1=w2=1,θ=2，则y=f(1∗x1+1∗x2−2)y=f(1*x_1+1*x_2 -2)y=f(1∗x1+1∗x2−2), 仅当x1=x2=1x_1=x_2=1x1=x2=1时， y=1y=1y=1;
- “或”：令w1=w2=1,θ=0.5w_1= w_2 = 1 , \theta=0.5w1=w2=1,θ=0.5, 则y=f(1∗x1+1∗x2−0.5)y=f(1*x_1+1*x_2 -0.5)y=f(1∗x1+1∗x2−0.5)仅当x1=1x_1=1x1=1或x2=1x_2=1x2=1时， y=1y=1y=1;
- “非”：令，w1=0.6， w2=0,θ=−0.5，w_1=0.6， \ w_2 = 0 , \theta=-0.5，w1=0.6， w2=0,θ=−0.5，则y=f(−0.6∗x1+0∗x2+0.5)y=f(-0.6*x_1+0*x_2 +0.5)y=f(−0.6∗x1+0∗x2+0.5), 仅当x1=1x_1=1x1=1时，y=0y=0y=0；x2=0x_2=0x2=0时， y=1y=1y=1;
感知机学习规则非常简单， 对训练样例(x,y)(x, y)(x,y), 若当前感知机的输出为y^\hat{y}y^, 则感知机权重将这样调整：
(1)wi←wi+Δwi w_i \gets w_i+\Delta w_i \tag{1} wi←wi+Δwi(1)(2)Δwi=η(y−y^)xi \Delta w_i = \eta(y - \hat{y})x_i\tag{2} Δwi=η(y−
最低0.47元/天 解锁文章
扫一扫
1273
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
