B, B-, B+树的定义，特性，联系与区别（红黑树）

B树的不同定义，有时B树即是B-树

为什么会有B树： 因为二叉树的查找平均时间是logN，是与二叉树的深度有关，所以为了减少二叉树的深度，增加查找速度，势必要增加树的叉树。如果该树是M叉的，M>2的话，logm(N)势必要小于log2(N),所以当数据量非常大的时候，B树的平均查找时间要少于二叉树。

红黑树：带有平衡性的二叉搜索树增强版

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

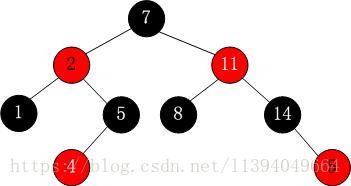
　　性质1. 节点是红色或黑色。

　　性质2. 根节点是黑色。

　　性质3 每个叶节点是黑色的。

　　性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

　　性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

要知道为什么这些特性确保了这个结果，注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

考虑一棵黑色高度为3的红黑树：从根结点到叶结点的最短路径长度显然是2(黑-黑-黑)，最长路径为4(黑-红-黑-红-黑)。由于性质4，不可能在最长路经中加入更多的黑色 结点， 此外根据性质3，红色结点的子结点必须是黑色的，因此在同一简单路径中不允许有两个连续的红色结点。综上，我们能够建立的最长路经将是一个红黑交替的路径。

由此我们可以得出结论：对于给定的黑色高度为n的红黑树，从根到叶结点的简单路径的最短长度为n-1，最大长度为2(n-1)。

B, B-, B+树总结：

B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；（关键字可以在非叶子节点和叶子节点）M指的是树的阶数

B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

 B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

性能比较：

性能相当，都等价于在关键字全集做一次二分查找；

B-树 改善了B树的平衡问题，

B+树比 B-树 更适合文件索引系统(结构上的改善)，

B*树比B+树改善了空间利用率。

红黑树和AVL树的比较：

红黑树：

(1)并不追求“完全平衡”——它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除操作。

(2)此外，由于它的设计，任何不平衡都会在三次旋转之内解决。红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同，但统计性能比AVL树更高。

AVL树：

(1)它的左子树和右子树都是AVL树，左子树和右子树的高度差不能超过1;

(2) 查找、插入和删除在平均和最坏情况下都是O(log n),增加和删除可能需要通过一次或多次树旋转来重新平衡这个树;

(3)一棵n个结点的AVL树的其高度保持在0(log2(n)),不会超过3/2log2(n+1)

一棵n个结点的AVL树的平均搜索长度保持在0(log2(n)).

一棵n个结点的AVL树删除一个结点做平衡化旋转所需要的时间为0(log2(n)).

B树

二叉排序树（Binary Sort Tree）又称二叉查找（二路搜索）树，也叫B树。　　它或者是一棵空树；或者是具有下列性质的二叉树：　　

(1)若左子树不空，则左子树上所