1. 问题引入
已知一批房屋销售数据,
面积( )
价格(万元) 2104 460 1416 232 1534 315 ... ... 852 178
对于一间面积为1250(该数据不在已知数据内)的房屋,我们该如何预测它的售价呢?一种直观的想法就是利用一条直线去拟合上述数据,然后对于新的数据,可以将直线上这个点对应的值输出作为预测值。
2. 概念和符号
训练样例(training example):一条房屋销售记录,用 表示;其中
表示;其中 表示特征向量,
表示特征向量, 表示样例的值。当样例有多个特征时(假设有n个特征),有
表示样例的值。当样例有多个特征时(假设有n个特征),有
训练集(training set):房屋销售记录集合,用X表示; ,m为训练样例数;
,m为训练样例数;
3. 线性回归
线性回归假设特征和结果满足线性关系
令 ,则有
,则有
这就是线性回归的模型。它的主要特点是假设函数既是变量 的线性方程也是参数
的线性方程也是参数 的线性方程。
的线性方程。
4. 训练模型
定义代价函数(Cost Function, 也叫Squared Error Function)
4.1 Gradient Descent(梯度下降法)
starts with some 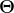 ;
;
repeats until convergence {
(Simultaneously update
)
}
我们还是以房屋销售为例来理解这个算法。先写出它的代价函数
下图是它的函数图像

我们再作出它的等高图

假设我们初始化 为图中小红叉所在的点,那么随着算法的进行,
为图中小红叉所在的点,那么随着算法的进行, 将沿着下图所示的路径移动,并最终移动到最低点。
将沿着下图所示的路径移动,并最终移动到最低点。

上面只是介绍了梯度算法的工作过程,那么它为什么可以有效工作呢?我们知道,对 求
求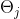 的偏导,其实就是计算
的偏导,其实就是计算 在
在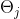 所在维度的斜率(或者讲
所在维度的斜率(或者讲 在任意一点的斜率沿
在任意一点的斜率沿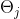 所在坐标轴的分量)。为了看的更清楚,我们以一个二次函数为例,
所在坐标轴的分量)。为了看的更清楚,我们以一个二次函数为例,

当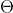 位于最低点左边(
位于最低点左边(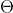 比
比 小)时,斜率为负,此时
小)时,斜率为负,此时 为正,
为正, 将变大,即
将变大,即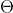 向
向 靠近;
靠近;
当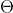 位于最低点右边(
位于最低点右边(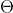 比
比 大)时,斜率为正,此时
大)时,斜率为正,此时 为负,
为负, 将变小,
将变小,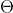 仍然向
仍然向 靠近;
靠近;
在梯度下降算法中还有一个重要的参数 (> 0)(Learning Rate),它控制了学习的速度。
(> 0)(Learning Rate),它控制了学习的速度。
当 较大时,
较大时, 可能并不总是变小(overshootting,如下图所示),最终可能不会收敛;
可能并不总是变小(overshootting,如下图所示),最终可能不会收敛;

当 较小时,收敛的速度会比较慢,最终可能需要较多的迭代才能收敛。由于在迭代的过程中
较小时,收敛的速度会比较慢,最终可能需要较多的迭代才能收敛。由于在迭代的过程中 越来越小,因此在选择好
越来越小,因此在选择好 后并不需要在学习的过程中调整
后并不需要在学习的过程中调整 的值。
的值。
当然,梯度下降法找到的只是一个局部最小值而并不一定是全局最小值,这取决于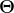 的初始值。下面的图说明选取的初值不同,最终到达的最优点也可能不同。
的初始值。下面的图说明选取的初值不同,最终到达的最优点也可能不同。

不过庆幸的是线性回归的代价函数一般都是凸函数,通过梯度下降的方法通常都可以找到最小值点。
4.2 Normal Equation
它的推导还是比较简单的。我们期望最好的情况是 ,表明假设函数与训练数据集完全一致,此时有
,表明假设函数与训练数据集完全一致,此时有
两边同时乘以 有
有
注意到 是一个方阵,等式两边再同时乘以这个方阵的逆矩阵可以得到
是一个方阵,等式两边再同时乘以这个方阵的逆矩阵可以得到
于是就可以得到
细心的读者可能会发现一个问题:如果按照上述的推导过程,最终会有 对所有的
对所有的 都成立。但在机器学习的过程中,这往往是不可能的。那么上述过程有什么不对呢?对的,
都成立。但在机器学习的过程中,这往往是不可能的。那么上述过程有什么不对呢?对的, 的逆矩阵不一定存在,但这并不影响Normal
Equation正常工作。在Octave里,即使一个矩阵的逆矩阵不存在,调用它的pinv函数依然可以得到它的伪逆矩阵。至于pinv是怎样实现的,作者也没有探究过,有兴趣的读者可以去研究下。
的逆矩阵不一定存在,但这并不影响Normal
Equation正常工作。在Octave里,即使一个矩阵的逆矩阵不存在,调用它的pinv函数依然可以得到它的伪逆矩阵。至于pinv是怎样实现的,作者也没有探究过,有兴趣的读者可以去研究下。
5. Feature Scaling
还是考虑房屋销售的例子,现在我们加入房间数目这个特征,
)
如果我们写出它的代价函数并作出它的等高图,

可以看到由于样例在两个特征上取值范围的差异,等高线几乎都是扁平的椭圆,这将导致梯度下降算法收敛的非常缓慢。为了克服这个缺点,我们可以对每一个特征进行缩放,使它们处于近似的数量级。缩放的方法可以是
其中 是特征向量第j维的平均值,
是特征向量第j维的平均值, 是特征向量第j维的标准差。
是特征向量第j维的标准差。
6. Regularization

如上图,假设training set有5个点,我们可以构造很多个假设函数模型,比如
(1)  (上图红线)
(上图红线)
(2)  (上图黑线)
(上图黑线)
(3)  (上图绿线)
(上图绿线)
如果单从代价函数的角度看, 无疑是最好的假设,因为它与training set完全拟合,代价几乎为0;但是这个模型过于复杂,对新数据的预测也很难与实际值符合,这是一个overfitting的例子;而
无疑是最好的假设,因为它与training set完全拟合,代价几乎为0;但是这个模型过于复杂,对新数据的预测也很难与实际值符合,这是一个overfitting的例子;而 过于简单,它的预测值与实际值存在较大的偏差。显然,
过于简单,它的预测值与实际值存在较大的偏差。显然, 才是我们最好要的模型。对于模型过于简单的问题,我们可以通过增加样例特征的方法来解决。那么,怎样避免模型过于复杂的问题呢?
才是我们最好要的模型。对于模型过于简单的问题,我们可以通过增加样例特征的方法来解决。那么,怎样避免模型过于复杂的问题呢?
我们把代价函数修改一下,为它增加一个regularization部分

上式中的第1部分要求假设函数尽量拟合训练集,而第2部分要求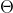 尽量小,以使假设函数尽量简单,避免出现overfitting。
尽量小,以使假设函数尽量简单,避免出现overfitting。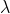 是regularization
parameter,是一个权重因子。
是regularization
parameter,是一个权重因子。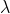 大,表示我们希望模型简单,这时会有大多数
大,表示我们希望模型简单,这时会有大多数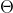 为0(或者接近0);
为0(或者接近0);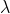 小,表示我们希望模型尽量拟合训练数据集。
小,表示我们希望模型尽量拟合训练数据集。
6.1 Gradient Descent with Regularization
starts with some 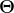 ;
;
repeats until convergence {
(Simultaneously update
)
}
6.2 Normal Equation with Regularization
7. 总结
Gradient Descent需要选择 ,需要多次迭代;而Normal Equation需要计算一次逆矩阵。当样例的特征比较多(n比较大时),使用Normal Equation会非常慢。一般情况下,当m >> n时,我们可以选择使用Normal
Equation。
,需要多次迭代;而Normal Equation需要计算一次逆矩阵。当样例的特征比较多(n比较大时),使用Normal Equation会非常慢。一般情况下,当m >> n时,我们可以选择使用Normal
Equation。





 这篇博客介绍了线性回归的概念,通过梯度下降法和正规方程训练模型,并探讨了特征缩放和正则化在防止过拟合中的作用,旨在预测未知房屋的售价。
这篇博客介绍了线性回归的概念,通过梯度下降法和正规方程训练模型,并探讨了特征缩放和正则化在防止过拟合中的作用,旨在预测未知房屋的售价。

















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








