(c语言实现)二叉树的相关操作 (三) 通过遍历构建二叉树的两种类型_in constructor 'treenode::treenode(int)':-优快云博客

本文介绍了如何使用C语言实现二叉树的相关操作，包括通过带标记的前序遍历构建二叉树，以及通过前序遍历和中序遍历构建二叉树。详细讨论了递归和非递归遍历方法，并提供了相关代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文所指二叉树皆为普通二叉树,下同

二叉树的定义

在介绍相关操作时,请记住一点,
二叉树构建核心思想是递归,

typedef char treeNodeType;
typedef struct _treeNode{
    struct _treeNode* left;
    struct _treeNode* right;
    treeNodeType value;
}treeNode;

相关操作有:

1 二叉树的先序,中序,后续遍历的递归版,使用栈循环版,还有使用队列层序遍历版
2 求二叉树某层的节点数,求二叉树的总节点数,求二叉树叶子节点数,**
3 求某节点的左右子节点或者父节点
3 将二叉树镜像翻转
4 判断一颗二叉树是否是完全二叉树
5 在二叉树中查找某节点
6 二叉树的深拷贝(clone)
7通过前序有标记空节点结果构建二叉树
8 通过前序中序遍历构建二叉树

这篇博客主要解决加粗部分,详细代码请参见
其中有完整头文件,源文件,和单元测试.
感谢!
剩余操作请参见
(c语言实现)二叉树的相关操作 (一) 二叉树的递归遍历和循环遍历

(c语言实现)二叉树的相关操作 (二) 二叉树节点操作

仅仅是通过前序遍历或者中序遍历后序遍历是无法确定一个二叉树的
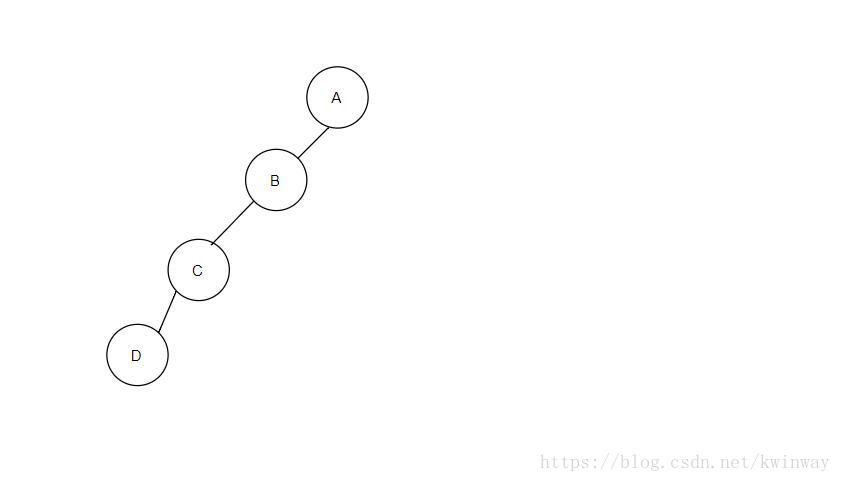
这里写图片描述
例如此树的前序遍历是ABCD
中序遍历是DCBA
后续遍历是DCBA

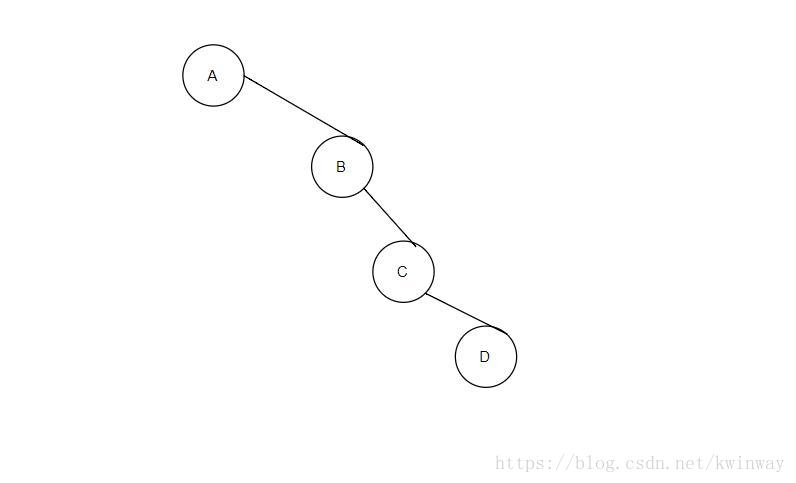
这里写图片描述
例如此树的
前序遍历是ABCD
中序遍历是ABCD
后续遍历是DCBA
他们的前序和后续遍历是一样的,然而树长得形态却不一样
但是倘若我们可以给树的空位置加上标记,就可以只用前序遍历或者后序遍历打印二叉树

通过带标记的前序遍历打印二叉树

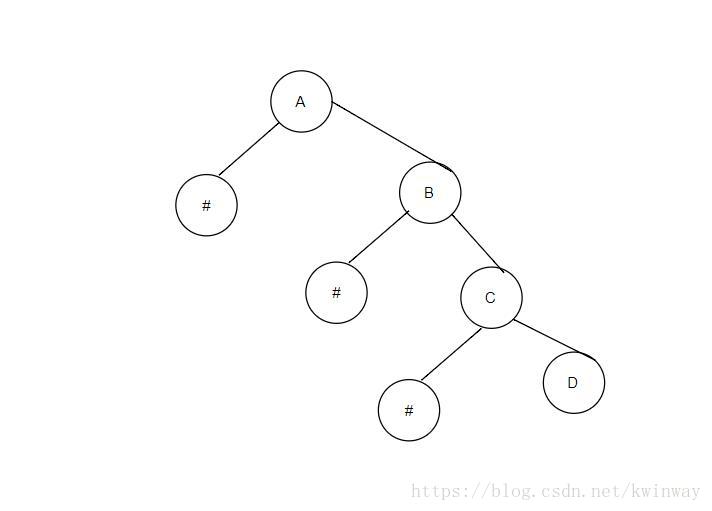
这里写图片描述
方便起见,我们使用#号标记空节点,如图所示,
此树的前序遍历结果就是 A#B#C#D
我们先从根节点开始,递归的创建节点, 并从前往后扫描前序遍历字符串
若碰到 # 就返回递归
注意一点,标记当前字符串的位置index应该传入其地址,
因为递归过程会开辟新的栈帧,保存新的变量,
若index是传值,在每次递归的栈帧中index值都不一样,会造成混乱的结果,
所以因将其地址传入,每次进行操作的是其本身,可以保证index从0到字符串结尾线性地递增

treeNode*  _ConstructTree(treeNode* node, char* str, int *index)
{
    if(( str+*index  )== '\000')
    {
        return NULL;
    }
    if(*(str+*index ) == '#')
    {
        return NULL;
    }
    node = (treeNode*)malloc(sizeof(treeNode));
    if(node == NULL)
        perror("malloc:");
    node->value = *( str + *index );
    (*index)++;
    node->left = _ConstructTree(node->left, str, index);
    (*index)++;
    node->right= _ConstructTree(node->right, str, index);
    return node;
}

通过前序遍历和中序遍历构建二叉树

我们可以看到,前面两个特殊的二叉树唯一的差别也就是中序遍历的结果不同,如果我们使用
前序遍历和中序遍历的信息,也可以准确的构建出一颗二叉树 前提条件是这颗二叉树的节点没有重复

char* pre_order = "ABDEGCF";
char* in_order = "DBGEACF";

可以看到前序遍历中第一个字母A肯定是根节点,那么在中序遍历中 A以前的肯定是其左子树,
A以后的肯定是其右子树,
其左子树为的
前序遍历为BDEG
中序遍历为DBGE
那么通过前序遍历得其左子树的的根节点就是B
通过中序遍历得知其左子树的左子树只有一个节点 D
其右子树为GE

分析道这不难发现可以通过递归解决问题,
我们需要传入的参数有

前序遍历的起始位置和终止位置,
中序遍历的其实位置和终止位置
当前序遍历中根节点对于中序遍历时根节点的偏移量为0是表示找到了叶子节点,

treeNode* constructTree(treeNode* node ,char* pre_start,char* pre_end,char*in_start, char* in_end)
{
    if(*pre_start == '\000' || *in_start == '\000')
    {
        return NULL;
    }
    node = malloc(sizeof(treeNode));
    treeNodeType root_value = pre_start[0];
    node->value = root_value;
    int offset = 0;
    while(pre_start[0] != in_start[0 + offset])
    {
    //计算偏移量
        offset++;
    }
    if(offset == 0)
    {
           //根节点
        return node ;
    }
    node->left = constructTree(node->left,pre_start + 1,pre_start+offset, in_start, in_start+offset - 1);
    node->right = constructTree(node->right,pre_start+offset + 1 , pre_end, in_start + offset + 1, in_end);
    return node;
}
void pre_order_function(treeNode* root)
{
    if(root == NULL)
        return;
    printf("%c ",root->value);
    pre_order_function(root->left);
    pre_order_function(root->right);
}