代码随想录算法训练营第二十四天|77. 组合

最新推荐文章于 2025-12-21 15:46:06 发布

原创最新推荐文章于 2025-12-21 15:46:06 发布 · 93 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #c++

代码随想录算法训练营专栏收录该内容

48 篇文章

订阅专栏

文章介绍了如何使用回溯法解决LeetCode中的77题——组合问题，通过回溯三部曲（递归函数定义、终止条件、单层搜索）以及剪枝策略，实现有效的路径探索，找到所有可能的k个数的组合。

LeetCode 77 组合

题目链接：https://leetcode.cn/problems/combinations/

思路：

将问题变成一个树形结构

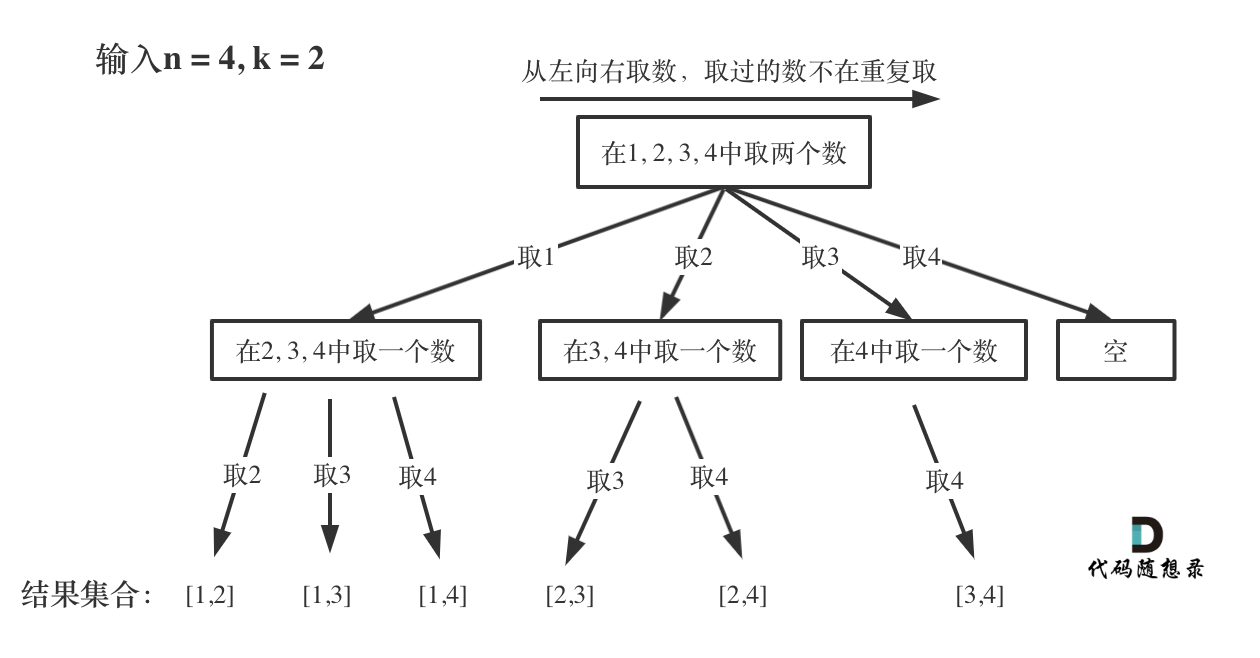
代码：

回溯三部曲：

递归函数的返回值以及参数

回溯函数(递归函数)终止条件

单层搜索的过程

基础回溯法

class Solution {
public:
    vector<int>path;
    vector<vector<int>>result;
    vector<vector<int>> combine(int n, int k) {
        path.clear();
        result.clear();
        backtracking(n,k,1);
        return result;
    }

    void backtracking(int n,int k,int startindex)
    {
        // 终止条件
        if(path.size()==k)
        {
            result.push_back(path);
            return;
        }

        // 单层搜索过程
        for(int i = startindex;i<=n;i++)    // for循环---纵向遍历
        {
            // 处理节点
            path.push_back(i);
            // 递归操作---向下遍历
            backtracking(n,k,i+1);
            // 回溯
            path.pop_back();
        }
        return ;
    }
};

剪枝后的回溯法

class Solution {
public:
    vector<int>path;
    vector<vector<int>>result;
    vector<vector<int>> combine(int n, int k) {
        path.clear();
        result.clear();
        backtracking(n,k,1);
        return result;
    }

    void backtracking(int n,int k,int startindex)
    {
        // 终止条件
        if(path.size()==k)
        {
            result.push_back(path);
            return;
        }

        // 单层搜索过程
        // for循环---纵向遍历
        for(int i = startindex;i<=n-(k-path.size())+1;i++)    // i<=n-(k-path.size())+1---剪枝操作
        {
            // 处理节点
            path.push_back(i);
            // 递归操作---向下遍历
            backtracking(n,k,i+1);
            // 回溯
            path.pop_back();
        }
        return ;
    }
};

今日总结：

在二叉树的时候接触过回溯，第一次接触完成的回溯法。学习到了回溯的基本模板，要记住回溯的基本模板，记住回溯三部曲和剪枝的方法。