机器学习(第6章 聚类分析)

一、学习目标

1.了解聚类算法的基本任务和聚类的一些基本依据

2.学习序贯方法的聚类

3.学习层次聚类算法

4.掌握K均值聚类算法

二、聚类概述

        1.聚类问题

        作为一种无监督机器学习的方法，其优势在于模型小、速度快，属于对数据预处理的一种方法：即将数据类似的样本汇聚在一起。这样有助于后续任务的进行。具体描述如下：

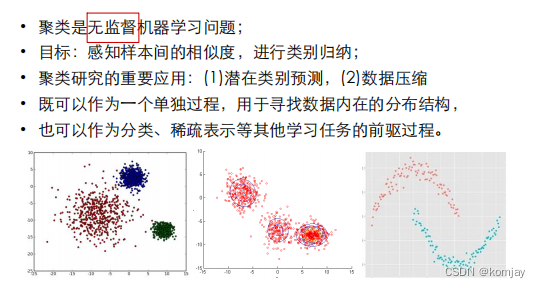
        在不同的学科中，聚类算法有不同的称呼：

        在聚类任务中，必须保证以下三个条件：（1）每个类别一定都有样本点、（2）所有样本点必属于某一类、（3）某个样本点只能属于一类。写成数学符号就是：

       2.相似性度量

        想要将样本点进行聚类，总需要定义一个评判标准，从而才能确定样本之间的相似性，这种评判标准我们称其为相似性度量。按照对象不同，我们有四种等级的相似性度量：

        （1）样本-样本度量。在聚类早期，并没有一些集合，于是需要定义样本与样本之间的相似性，来进行聚类，可以使用的度量有：

        （2）样本-集合度量。可以使用的度量有：

        （3）集合-集合度量，又称类间距离，这个并不是用来合并两个集合（当然也确实可以，但实际操作中不常这么合并，容易产生一个大集合），而是聚类后用于评判聚类聚得好不好（后面会细讲），可以用的度量有：

        （4）集合内样本间距离度量，又称类内距离，跟（3）一样，也是用来衡量聚类算法的好坏的，其度量公式有两种，一般还是用第一种：

        3.内部指标

        使用类间距离和类内距离，我们就有了评判聚类算法好坏的内部指标：

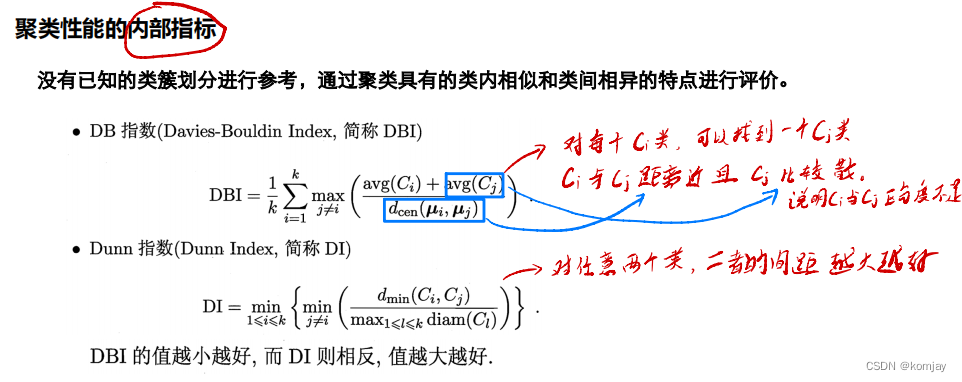
        4.外部指标

        由于聚类是无监督学习，样本的标签就相当于是外部信息，如果评价聚类时加入标签判定，则称为外部指标度量。由于聚类终究是聚类，而不是分类，得不到样本对应的是什么标签，只能得到两个样本是不是同一类。于是就将样本两两判定，划分成a，b，c，d四类。其中只有a的数量越多越好，b，c越少越好，d无法决定好坏，具体流程如下：

        可以用下面三种外部指标来确定聚类的好坏：

        

三、序贯方法

        1.经典得序贯方法

        算法思想：逐个比较单个样本与类簇的相似性，有相似类则归类，无相似类就新建一个类簇。整体算法如下：

        好处在于速度快、算法简单。缺点也很明显：当初始的点选择不好时，比如每个点离上一个点得距离卡得刚刚好，把这些点都归为了一个大类，这样不利于后续点划分成新得类。于是我们提出一种改进：先进行类别确定，再将剩余点分类。

        2.步骤划分的序贯方法

·        算法思想：分为两步，第一步类别确定：过一遍所有的样本点，将距离超过阈值的点来创建类簇，没超过阈值的忽略；第二部分类：将剩余的样本点划分到最近的类簇中。整体算法流程如下：

        算法还是有一个缺点：太依赖人为设置的超参数，即距离阈值了。于是再做改进，使用双阈值方法，形成灰色带区域。

        3.双阈值序贯方法

        算法思想：设置两个距离阈值Θ1和Θ2，样本点离其最近的类簇的距离如果在两阈值之间，则形成灰色带，在灰色带中再进行新一轮的类簇划分。思想如下：

四、层次聚类

        1.基本思想

        首先要了解聚类划分和聚类嵌套的定义：

        聚类划分和嵌套可以通过上面的例子来理解，通过观察R1和R2，可以知道，R2嵌套R1，则说明对R2作更细致的划分可以得到R1。

        而层次聚类的基本思想就基于这样一条规律：

        2.归并算法

        算法思想：初始时将每个样本点都当中单独的一个类簇，每次迭代先计算两个类簇之间的相似性，然后将最相似的两个类簇合并，最后可以将所有点合并到一个类簇中，当然，可以人工设置得到几个类簇就停止。整体算法如下：

        有一个比较明显的缺点：

        于是提出改进：用矩阵来保存相似性，避免重复计算：

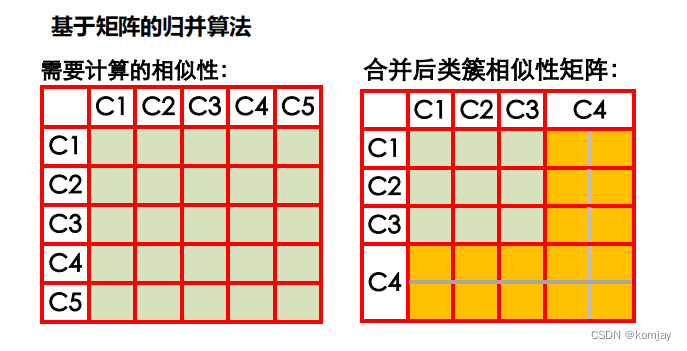
        最后的归并算法如下：

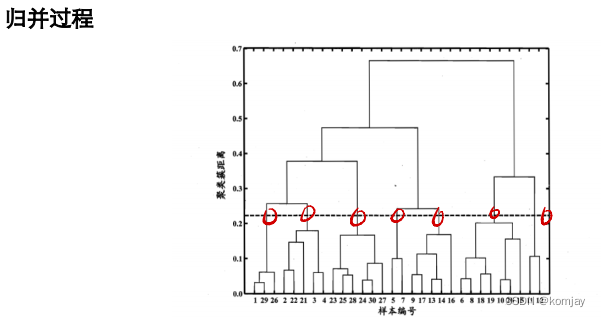
        例子如下：（从上往下）

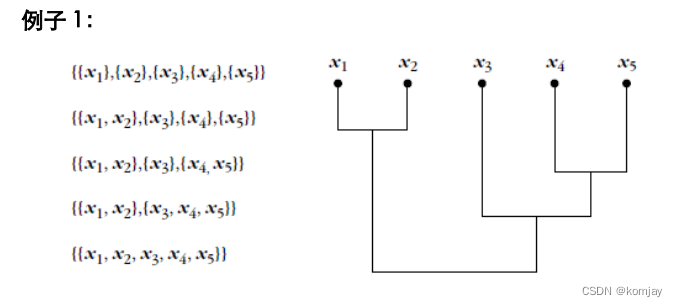
        3.分化算法

        算法思路：初始时将所有的样本点归为一个类，如果有n个样本点，则有2^(n-1)-1种划分，计算每个划分中，划分的两个类簇的相似性，选择最不相似的划分作为下一步的开始，迭代进行。整体算法你过程如下：

        同样也有重复计算的缺点，同样可以用矩阵来解决。这里就不赘述了。例子如下：（从上往下进行）

五、K均值聚类

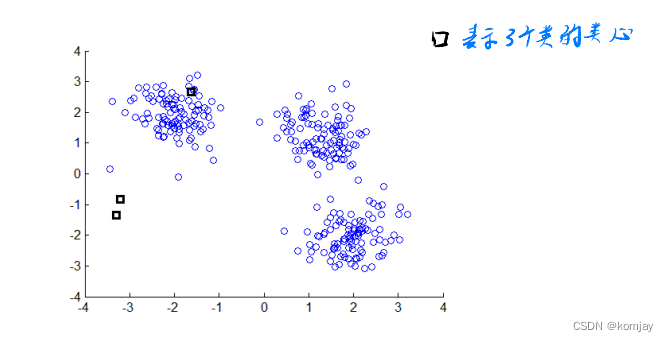
        算法思想：有n个样本和初始化k个聚类中心点，进行迭代：将离第k个中心点的最近的样本点划分为第k类，然后将每个类的样本点进行取平均，得到新的中心点。重复上面的迭代到中心点不移动。以一个例子来说明：

        （1）初始化3个中心点，并找到离其分别最近的点

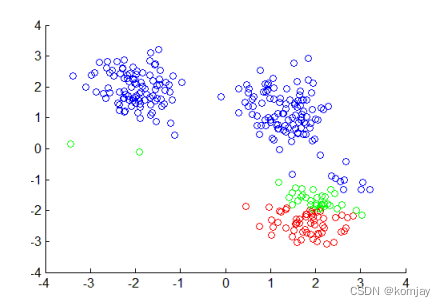
        （2）计算新的3个中心点并再次找到离其分别最近的点

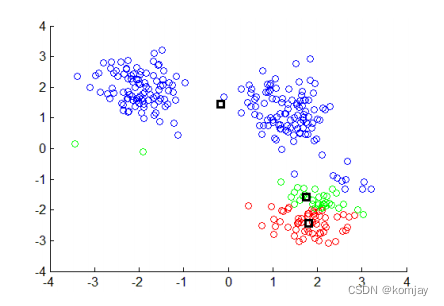
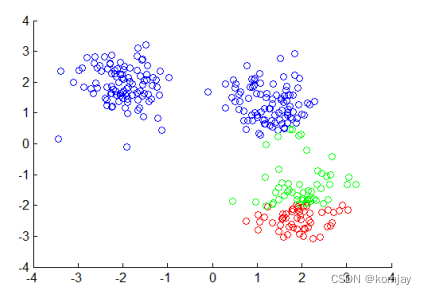
        （3）重复（2），可以发现绿色开始往上移动

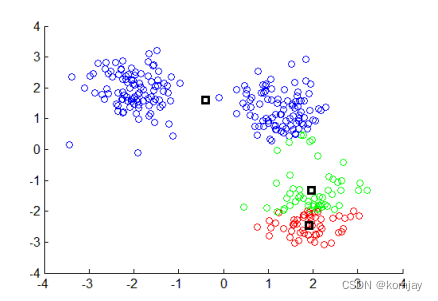
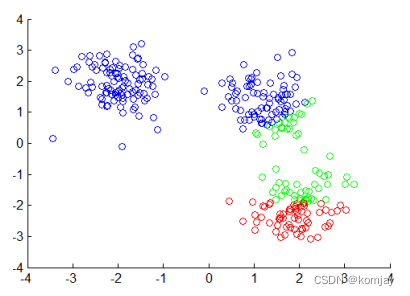
        （end）重复n步直到中心点不再移动，可以得到最后的聚类结果：

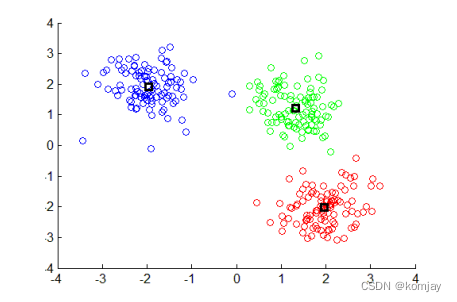
        所以K-means算法的一般性流程如下：

        这是一个非常像EM算法的聚类算法，其十分强大，但也有问题：

       （1）问题是可以通过人为调整来解决，而（2）问题需要从算法层面来解决。于是针对（2）问题，提出了改进方法：单个划分最优原则。我们的目标函数就是追求Je加和最小。

 

六、本章小结

        了解聚类的任务与目标，学习了三种用于聚类的方法：序贯方法、层次聚类和K均值聚类。并针对其各自的问题提出了各种改进手段。