算法中的最优化方法和实现 (第8、9课 凸优化)

一、学习目标

1.回顾一下什么凸函数，了解凸函数与凸优化的关系

2.学习各种凸优化算法：切平面法、椭圆法、内点法

二、凸优化的定义

只有当目标函数和约束函数都是凸函数时，这个规划问题就是凸优化。

关于凸函数的一些确定方法：

三、切平面法（Cutting-plane algorithm）

算法思想：随机取目标函数上的点，做这些点的切线，将这些切线连接，形成目标函数的下界，对约束函数也进行同样的操作，将折线中的最小值点作为新的点再做切线，迭代至折线最小值点对应的目标函数和折线值小于阈值。做切线如图所示：

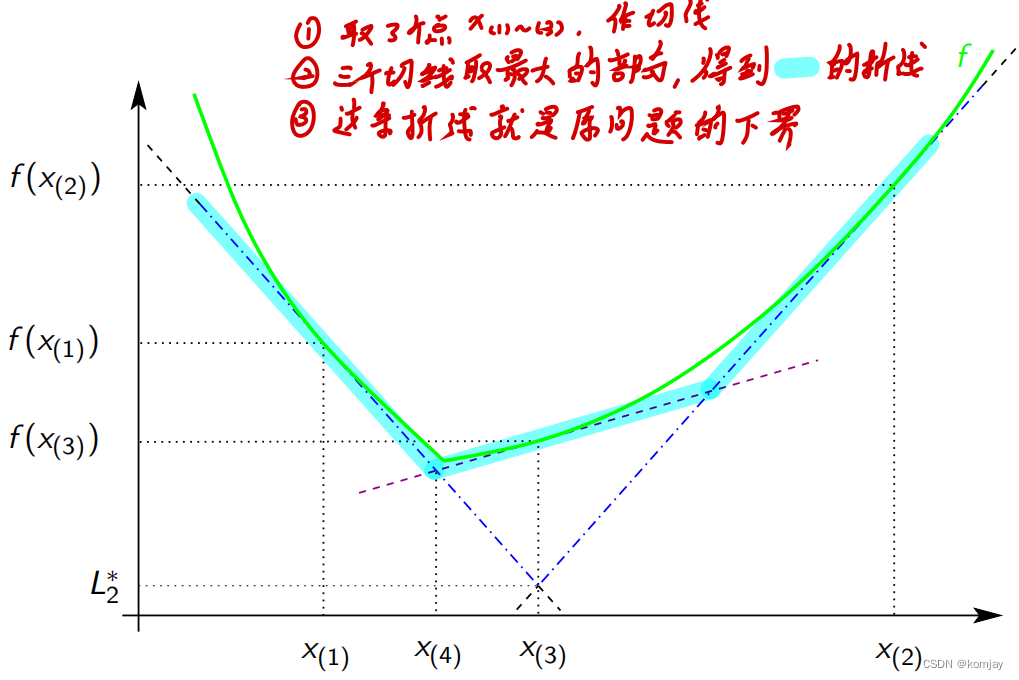
然后挑选出折线中最小值点x*：

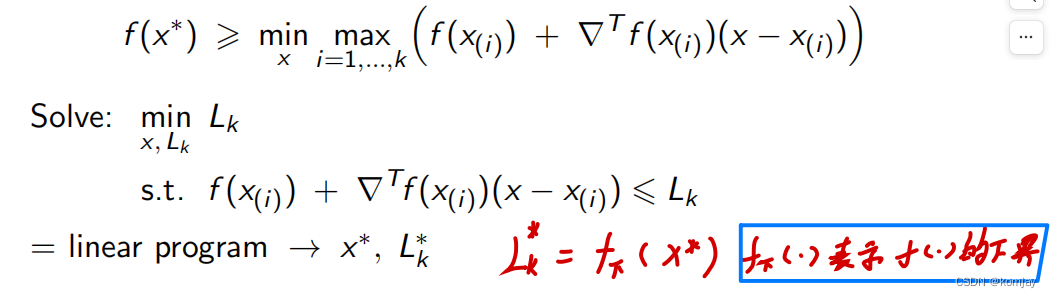
再然后将x*作切线，重复上面步骤找到新的x*：