删除操作
1. 在纯函数式的环境下,纯函数式的数据结构决定了树不是真的被改变了,实际上是重建一棵树。(大多数函数式编程环境使用一种名叫Persistent的方法,可以复用树中没有改变的部分,从而减小重建的开销)。
利用一个双重黑色的引入。将删除节点的颜色(黑色)保存在其父节点中,如果父节点红色,则染成黑色,如果父节点是黑色,就是双重黑色。
2、结点的兄弟结点为红色;
3、结点的兄弟结点为黑色,同时其子结点也均为黑色;
4、结点的兄弟结点为黑色,同时兄弟结点的左子结点为红色,右子结点为黑色;
5、结点的兄弟结点为黑色,同时兄弟结点的右子结点为红色,左子结点为红色;删除之后通过调整,改变旋转和调整颜色维持红黑树的性质。
注意:x是指向于非根节点的一个双重黑色的节点。
情形3:x(A)的兄弟节点w(D)是黑色,兄弟节点的左子节点(C)为红色, 右子节点(D)为黑色。
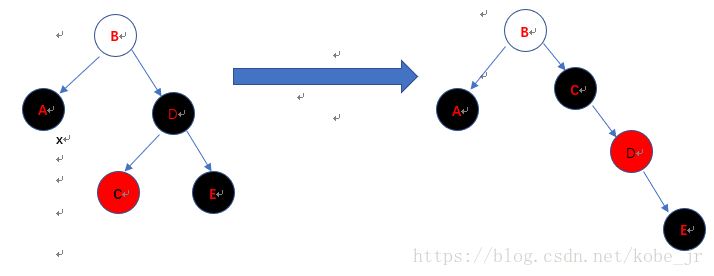
此时交换w.left.color(C)和w.color(D)的颜色,然后右旋。
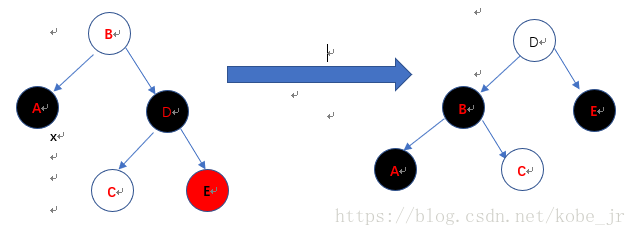
情形4:兄弟节点的右子节点是红色
1. 在纯函数式的环境下,纯函数式的数据结构决定了树不是真的被改变了,实际上是重建一棵树。(大多数函数式编程环境使用一种名叫Persistent的方法,可以复用树中没有改变的部分,从而减小重建的开销)。
利用一个双重黑色的引入。将删除节点的颜色(黑色)保存在其父节点中,如果父节点红色,则染成黑色,如果父节点是黑色,就是双重黑色。
删除的过程:1、如果删除的这个节点是根节点,root = null。左右节点都为空,直接删除。直接删注意它的颜色是否为黑色,若是黑色删除了违反性质5;
2、如果删除的这个节点有一个子节点,让它的子节点替代它,再把它删除即可;
3、删除的节点的左右子节点都不是空,找他的替代节点(可能是它的左子节点,或者左子节点的右节点一直遍历下去,即左子树的max, 亦或是右子树的min),然后替代节点替代这个值,将删除节点删除。
删掉后的结果则分为好几种情况(下面的结点为替代替代结点后的结点):
1、结点为新的根,此时只是将所有的路径中都去除一个黑色结点,所以依然保持平衡;2、结点的兄弟结点为红色;
3、结点的兄弟结点为黑色,同时其子结点也均为黑色;
4、结点的兄弟结点为黑色,同时兄弟结点的左子结点为红色,右子结点为黑色;
5、结点的兄弟结点为黑色,同时兄弟结点的右子结点为红色,左子结点为红色;删除之后通过调整,改变旋转和调整颜色维持红黑树的性质。
注意:x是指向于非根节点的一个双重黑色的节点。
情形1:x(A)的兄弟节点w(D)是红色的。
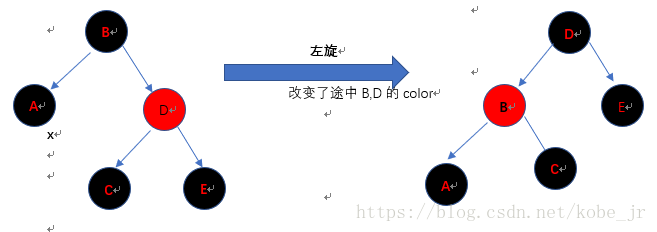
情形2:x(A)的兄弟节点w(D)是黑色的,它的两个子节点C、E也是黑色的。
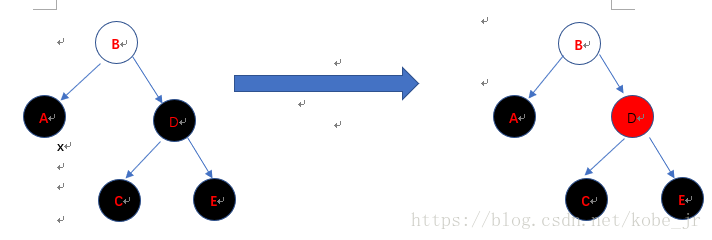
情形3:x(A)的兄弟节点w(D)是黑色,兄弟节点的左子节点(C)为红色, 右子节点(D)为黑色。

此时交换w.left.color(C)和w.color(D)的颜色,然后右旋。
情形4:兄弟节点的右子节点是红色

左旋。x(A)褪去一层黑色变为单黑色。B节点变为黑色。当x设置为根后,当while循环测试其循环条件时,结束循环。
参考代码:
//删除指定节点
public void delete(T element){
//获取要删除的节点 注意这里是通过查找而不是new
Node target = tree_search(element);
if(target.left != null && target.right != null){
//先找到目标节点中序遍历的前一个节点
//前一个节点显然在它的左子树中。相当于找左子树的最大值。
Node tmp = target.left;
while(tmp.right != null){
tmp = tmp.right;
}
target.data = tmp.data;
target = tmp;
}
// System.out.println(target);
//修复它的替换节点,如果该替换节点不为Null
Node replacement = (target.left != null ? target.left : target.right);
// System.out.println(replacement); --可以为null
if(replacement != null){
replacement.parent = target.parent;
//如果目标节点的父节点为null,那么目标节点自己是根节点
if(target.parent == null){
root = replacement;
}
//如果target是其父节点的左节点
else if(target == target.parent.left){
target.parent.left = replacement;
}
else{
target.parent.right = replacement;
}
//删除这个节点
target.left = target.right = target.parent = null;
//修复红黑树
if(target.color == BLACK){
rbDelect_Fixup(replacement);
}
}
//自身是根节点
else if(target.parent == null){
root = null;
}
else{
//target无子节点,把它当成虚的替换节点
//修复红黑树
if(target.color == BLACK){
rbDelect_Fixup(target);
}
if(target.parent != null){
if(target ==target.parent.left){
target.parent.left = null;
}
else if(target ==target.parent.right){
target.parent.right = null;
}
target.parent = null;
}
}
}//删除节点后修复红黑树
private void rbDelect_Fixup(Node T) {
while(T != root && colorOf(T) == BLACK){
//T是其父节点的左节点
if(T == leftOf(parentOf(T))){
//获取它的兄弟节点
Node brother = rightOf(parentOf(T));
if(brother.color == RED){
//兄弟节点设置为黑色。
setColor(brother, BLACK);
//父节点设置为红色
setColor(parentOf(T), RED);
rotateLeft(parentOf(T));
//将兄弟节点设置为删除节点的父节点的右节点。
brother = rightOf(parentOf(T));
}
if(colorOf(leftOf(brother)) == BLACK && colorOf(rightOf(brother)) == BLACK){
//
setColor(brother, RED);
T = parentOf(T);
}
else{
//只有兄弟节点的右节点是黑色
if(colorOf(rightOf(brother)) == BLACK){
//左节点也设置为黑色
setColor(leftOf(brother), BLACK);
setColor(brother, RED);
rotateRight(brother);
brother = rightOf(parentOf(T));
}
//设置兄弟接待你的颜色和父节点一样
setColor(brother, colorOf(parentOf(T)));
//T的父节点设置成黑色
setColor(parentOf(T), BLACK);
//brother的右节点设置为黑色
setColor(rightOf(brother), BLACK);
rotateLeft(parentOf(T));
T = root;
}
}
//如果T是其父节点的右子节点
else{
//获取T的兄弟节点
Node brother = leftOf(parentOf(T));
if(brother.color == RED){
//兄弟节点设置为黑色。
setColor(brother, BLACK);
//父节点设置为红色
setColor(parentOf(T), RED);
rotateRight(parentOf(T));
//将兄弟节点设置为删除节点的父节点的右节点。
brother = leftOf(parentOf(T));
}
if(colorOf(leftOf(brother)) == BLACK && colorOf(rightOf(brother)) == BLACK){
setColor(brother, RED);
T = parentOf(T);
}
else{
//只有兄弟节点的左节点是黑色
if(colorOf(leftOf(brother)) == BLACK){
//brother的右节点也设置为黑色
setColor(rightOf(brother), BLACK);
setColor(brother, RED);
rotateLeft(brother);
brother = leftOf(parentOf(T));
}
//设置兄弟接待你的颜色和父节点一样
setColor(brother, colorOf(parentOf(T)));
//T的父节点设置成黑色
setColor(parentOf(T), BLACK);
//brother的右节点设置为黑色
setColor(rightOf(brother), BLACK);
rotateLeft(parentOf(T));
T = root;
}
}
}
setColor(T, BLACK);
}参考书籍:《算法导论》《疯狂Java突破程序员基本功的16课》
以上就是这篇的主要内容,欢迎提出意见,此外图片制作粗糙,请见谅。谢谢!























 177万+
177万+










