目录
1.模型的参数估计方法
- 极大似然估计法
极大似然的基本思想是:一个随机试验如有若干个可能的结果A、B、C、… ,一次试验中若出现结果A,则认为实验条件对A的出现有利,也即该实验条件下A出现的概率P(A)较大。而极大似然估计就是要找到A出现概率最大值所对应的实验条件。 - 贝叶斯估计法
即利用贝叶斯定理结合先验概率及新的证据(一般指数据的似然函数),得到新的概率。 - 最大后验估计
Maximum A Posteriori,即MAP,也称最大后验点估计。
最大后验估计可以看作规则化的最大似然估计。
原则上,我们应该用参数θ \thetaθ的完整贝叶斯后验分布进行预测,这就是贝叶斯估计。但是单点估计常常也是需要的,这是因为通常贝叶斯后验的计算对于大多数有意义的模型来说是困难的。这个时候就考虑用点估计求得一个近似解。由此,结合贝叶斯估计的优点,提出了最大后验点估计的方法。
2.因果推断
事件与变量的关系主要是相关和因果的。
相关性是指X在观测数据分布中与Y相关。如果观察X的分布,就可以推断y的分布。
因果性是指操作/改变X之后,Y也随着这个操作/改变而改变,也就是说X是Y的原因。
在常用的机器学习算法中,关注的是特征之间的相关性,没有办法识别特征之间的因果性。然而在做决定和判断时,我们需要因果关系。
因果推断的方法
(1)A/B Test
如果可能,尽可能使用随机实验
以推荐算法为例判断推荐算法是否有效,ABTest将用户随机分为两组,分别应用不同的算法,通过判断两组用户点击率的差异来估计因果效应。通过随机分组,消除了易混淆变量的影响。
A/B Test,简单来说就是针对同一个产品目标制定两个方案(比如两个网页一个带红色按钮,一个带蓝色按钮),让一部分用户使用方案A,其他用户使用方案B,然后通过日志记录用户的使用情况,通过结构化日志数据分析点击率、转化率等相关指标,使方案更符合预期的设计目标,最终将所有流量转换到符合目标的方案中去。
(2)断点回归Regression discontinuity
无法进行随机实验时,则可以进行自然实验(如断点回归……)
断点回归是自然实验中的一种观察方法,简单理解就是在回归过程中,观察在临界点处是否出现断层/断点。
举一个简单的例子,假设现在有一个产品,收集500个金币后就可以得到一个勋章,现在要判断有无勋章对用户在线时长的影响。
断点回归法观察金币在500附近的用户,如497到502,观察【接近500但小于500(无勋章)】与【接近500但大于500(有勋章)】的用户在线时长是否有显著区别,若有,说明有勋章很可能会增加用户的在线时长。
(3)倾向得分匹配Propensity score matching
如果自然实验也无法进行,考虑使用基于条件的方法(倾向得分匹配……)
当条件变量很多的时候,可以考虑使用倾向得分匹配。
以推荐算法为例,当条件变量很多的时候,通过逻辑回归等方法对这些变量进行训练,并计算出一个倾向得分,在这里是用户被施加新算法的概率。
倾向得分匹配的一般步骤如下:
1.尽可能完整的绘制出变量之间的因果图
2.选择影响要判断因果性的变量的条件变量
3.对用户进行分层/分组,满足组内的用户计算得出的倾向得分接近
比较两组用户的输出,计算因果效应。
3.使用平均数和使用中位数的区别
平均数与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动。主要缺点是易受极端值的影响,这里的极端值是指偏大或偏小数,当出现偏大数时,平均数将会被抬高,当出现偏小数时,平均数会降低。
中位数与数据的排列位置有关,某些数据的变动对它没有影响;它是一组数据中间位置上的代表值,不受数据极端值的影响。
4.回归分析的五个基本假设
1.线性性 & 可加性
假设因变量为Y,自变量为X1,X2,则回归分析的默认假设为Y=b+a1X1+a2X2+ε。
线性性:X1每变动一个单位,Y相应变动a1个单位,与X1的绝对数值大小无关。
可加性:X1对Y的影响是独立于其他自变量(如X2)的。
2.误差项(ε)之间应相互独立。
若不满足这一特性,我们称模型具有自相关性(Autocorrelation)。
3.自变量(X1,X2)之间应相互独立。
若不满足这一特性,我们称模型具有多重共线性性(Multicollinearity)。
4.误差项(ε)的方差应为常数。
若满足这一特性,我们称模型具有同方差性(Homoskedasticity),若不满足,则为异方差性(Heteroskedasticity)。
5.误差项(ε)应呈正态分布。
5.CLT中心极限定理
CLT中心极限定理论证随机变量的和的极限分布是正态分布。
中心极限定理告诉我们,当样本量足够大时,样本均值的分布慢慢变成正态分布。
中心极限定理是说:
样本的平均值约等于总体的平均值。
不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的整体平均值周围,并且呈正态分布。据此,我们可以用样本对总体进行估计。
根据中心极限定理,我们可以得出的结论是:
1.用样本来估计总体。
任何一个样本的平均值将会约等于其所在总体的平均值。
2.样本平均值呈正态分布
中心极限定理也就是这么两句话:
1)任何一个样本的平均值将会约等于其所在总体的平均值。
2)不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的平均值周围,并且呈正态分布。
中心极限定理有什么用呢?
1)在没有办法得到总体全部数据的情况下,我们可以用样本来估计总体。
2)根据总体的平均值和标准差,判断某个样本是否属于总体。
注意:中心极限定理要求n充分大,但是多大才叫充分大呢?一般在统计学中n>=30称之为大样本(统计学中的一种经验说法)。因此在实际生产中,不用多想,肯定都是大样本。
6.小数定律和大数定律
小数定律:如果统计数据很少,那么事件就表现为各种极端情况,而这些情况都是偶然事件,跟它的期望值一点关系都没有。
大数定律说如果统计数据足够大,那么事物出现的频率就能无限接近他的期望值。
大数定律说的是随机现象平均结果稳定性。
大数定律讲的是样本均值收敛到总体均值(就是期望)。
7.期望
某个事件的期望值,也就是收益,实际上是所有不同结果的和,其中每个结果都是由各自的概率和收益相乘而来。期望就是预期值。期望的本质是概率的平均值。
8.正态分布、指数分布
8.1正态分布
并非所有的数据都是连续的,根据数据类型的不同,有不同的求概率的方法,对于离散型随机变量的概率分布,我们关心的是取某一个特定数值下的概率,而对于连续型随机变量的概率分布,我们关心的是取某一个特定范围内的概率。
连续型随机变量的理想模型就是正态分布。
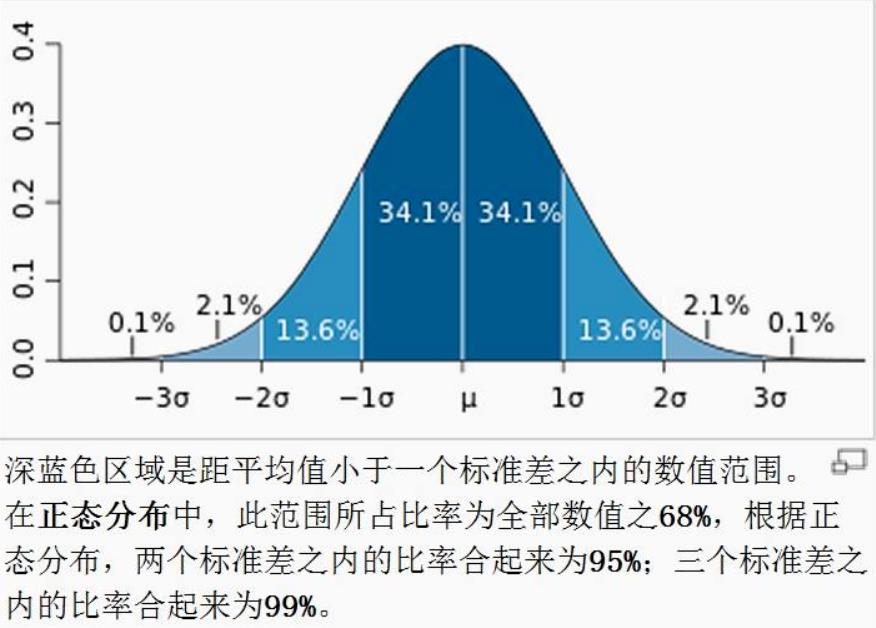
标准正态分布的意义是,任何一个正态分布都可以通过线性变换转换为标准正态分布。
8.2指数分布
指数分布是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。如旅客进机场的时间间隔,还有许多电子产品的寿命分布一般服从指数分布。
9.参数估计
“推断统计”研究的是用样本数据去推断总体数量特征的一种方法。
在实际研究中,总体数据的获取往往是比较困难的,总体参数一般也是未知的。因此,我们就需要利用总体的某个样本,通过样本统计量去估计总体参数。
- 参数估计:用样本统计量去估计总体的参数。比如,用样本均值去估计总体均值,用样本方差去估计总体方差。
- 点估计:用样本统计量的某个取值,直接作为总体参数的估计值。
- 区间估计:在点估计的基础之上,给出总体参数估计值的一个区间范围,该区间通常由样本统计量加减估计误差得到。
“小概率事件”指的就是在一次随机试验中,几乎不可能发生。
10.置信区间
置信区间:不是给出总体均值的精确估计,而是指出总体均值介于数值a和数值b之间。(a,b)被称为置信区间。
求解置信区间的四步骤:
1.选择总体统计量
2.求出其抽样分布
3.决定置信水平
4.求出置信上下限
11.假设检验
假设检验(显著性检验)的步骤:
1.确定要进行检验的假设
2.选择检验统计量
3.确定用于做决策的拒绝域
4.求出检验统计量的p值
5.查看样本结果是否位于拒绝域内
6.作出决策
显著性水平(使用α表示):表明你希望在观察结果的不可能程度达到多大时拒绝原假设H0
p值:取得样本中的各个结果或者取得拒绝域方向上的某些更为极端的结果的概率。
当P-Value的值大于α时,接受原假设。当P-Value的值小于α时,拒绝原假设。简单记为:p值越小越拒绝原假设。
假设检验的基本方法:
选取一个断言,对其进行检验——评估对其不利的证据。如果有足够的不利证据,则否定该断言;如果没有足够的不利证据,则接受该断言。
第一类错误:拒绝了真的原假设
第二类错误:接受了假的原假设
常用的假设检验:
1.单个正态总体均值的假设检验法(Z检验:方差已知)
Z检验用来判断样本均值是否与总体均值具有显著性差异。Z检验是通过正态分布的理论来推断差异发生的概率,从而比较两个均值的差异是否显著。Z检验适用于:
总体呈正态分布。
总体方差已知。
样本容量较大。
2.单个正态总体均值的假设检验法(t检验:方差未知)
t检验,与Z检验类似,用来判断样本均值是否与总体均值具有显替性差异。不过,t检验是基于t分布的。检验适用于:
总体呈正态分布。
总体方差未知。
样本容量较小。
3.卡方检验
卡方检验就是检验两个变量之间有没有关系。
卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,如果卡方值越大,二者偏差程度越大;反之,二者偏差越小;若两个值完全相等时,卡方值就为0,表明理论值完全符合。
通俗解释p值:
假设检验
假设:硬币是公平的
检验:认为假设是成立的,然后扔十次,看结果与假设是否相符
把八次正面的概率,与更极端的九次正面、十次正面的概率加起来,得到的就是(单侧P值):
p-value=P(8≤X≤10)=0.05
出现两次正面、一次正面、零次正面的概率也是很极端的:(双侧P值):
p-value=P(0≤X≤2)+P(8≤X≤10)=0.1
我们一般认为
p-value≤0.05
就可以认为假设是不正确的。
0.05这个标准就是显著水平
上面的扔硬币的例子,如果取单侧P值,那么根据我们的计算,如果扔10次出现9次正面:
p-value=P(9≤X≤10)=0.01≤0.05
我们可以认为刚开始的假设错的很“显著”,也就是“硬币是不公平的”。
如果扔10次出现出现8次正面:
p-value=P(8≤X≤10)=0.05≤0.05
这个和我们的显著水平是一样的啊,我们也可以拒绝假设,只是没有那么“显著”了。
置信区间,目的是根据样本构造一个区间,然后希望这个区间可以把真值包含进去,但是并不知道这个真值是多少。
而假设检验,则是假设真值是多少,然后检验这个假设是否可能为真。
























 857
857

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








