运筹系列28：网络单纯形法

1. network program问题

详情可参考这里
我们常常遇到的Assignment、Transportation、Maximum flow、Shortest path等问题都具有特殊的结构，可以用network program来建模。具体来说，network program指的是如下问题：
$\min c^{T}x$
$Ax=b$
$l\le x\le u$
其中$A\in {-1,0,1}^{n\times m}$，并且每一行只有一个1和一个-1。
下面是一个例子：

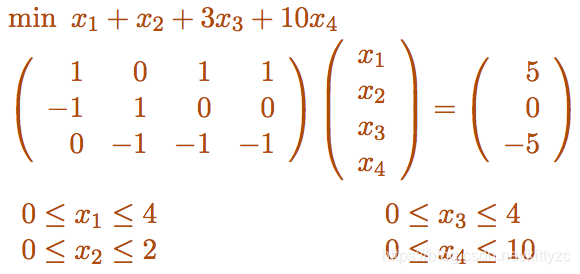
network program可以看做是最小费用流问题的数学模型。定义有向图$G=(V,E)$，$V$用行表示，$E$用列表示，从$i$到$k$有边的话，则有一列的第$i$行是1，第$k$行是-1。$x_j$表示第$j$条边上的流量，如下图：

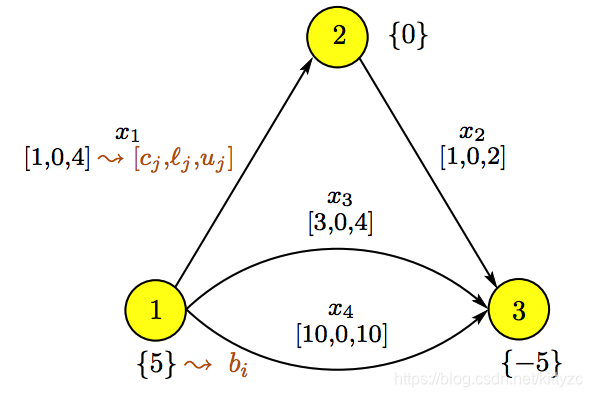
对于这类问题，如果存在一条path，那么$\Sigma$方向*边 = $e_{终点}-e_{起点}$，其中$e$表示单位向量。
定理：每一个连通图都有一个伸展树（包含所有节点的树）
定理：树的$A$的列相互线性独立，秩为（节点数-1）。

2. 求解方法

选择一个根节点，添加虚拟变量$w$和单位向量，如下：

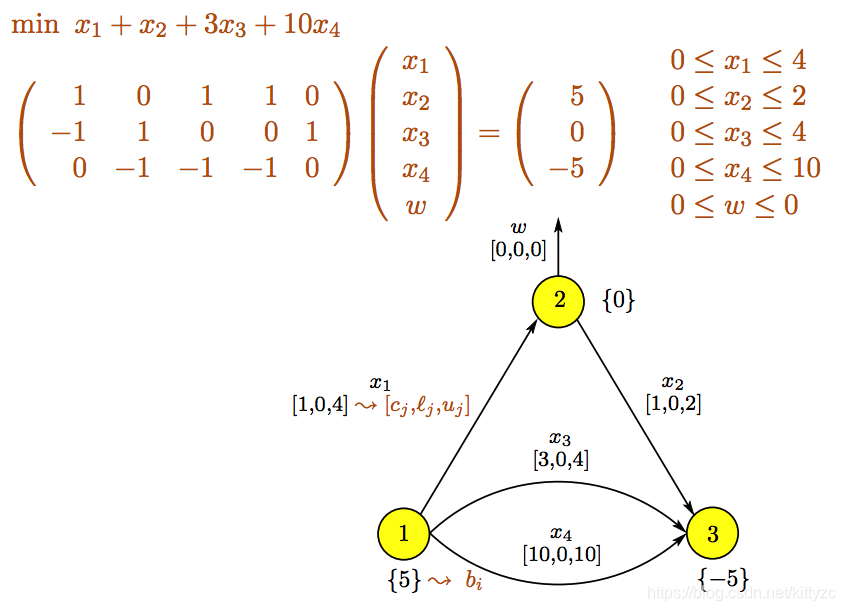
根节点衍生出的伸展树和$e_w$构成一组基$B$。我们回忆一下单纯形法的出入基过程：
每次将负数残差$c_N^T-c_B^T{B}^{-1}N$最小（绝对值最大）的非基变量$x_i$替换为基变量，同时将$(\frac{B^{-1}b}{(B^{-1}N{)}_i}{)}_j$最小值对应的基变量$x_j$替换为非基变量。
有3个地方用到$B^{-1}$：
$y^{T}B=c_B^T$
$Bx=N_q$
$Bx=b$
这三个地方都可以用上面的图快速求解，不需要再存储$B^{-1}$。以$y^{T}B=c_B^T$为例：

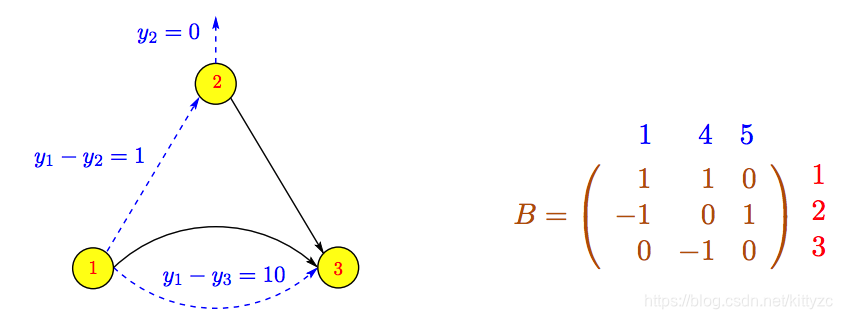
我们有：

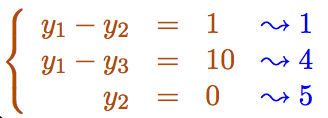
相当于从$y_2$出发遍历树。