这个系列好久没更了,当时停更是因为没有阅读量,但是我现在其实也不为了阅读量了,愿意写啥,写啥,所以就把这个系列又捡起来了(我之前留的所有坑,每个系列也都会填上的)
之前的文章介绍了MAE和MSE,这俩玩意都是做回归的
再复习一下
这次换一个公式写法为了好理解,我们用单样本损失
yi 就是y_true,y_i^就是预测值,对单个样本ii,有一个损失ℓ_iℓii
如果是回归 + MAE
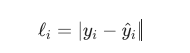
数学特点:
线性误差:误差每增大一点,惩罚线性增加,不会像平方那样放大极端值。
导数是符号函数:

在 0 点有“尖角”,对梯度下降不如 MSE 那么平滑。
适用场景:
回归任务,但:
函数曲线这样
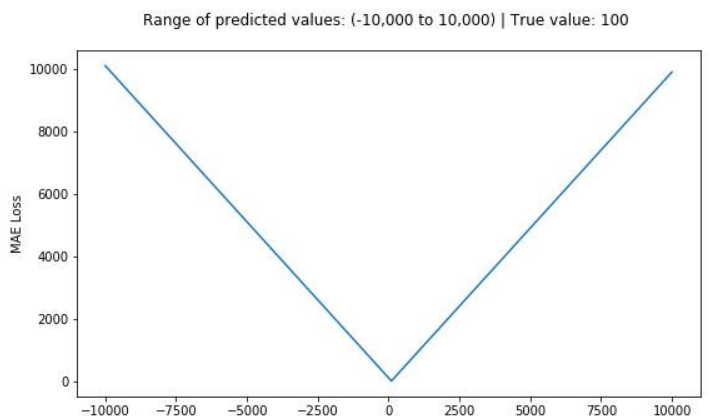
如果是回归 + MSE:
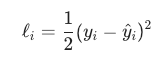
数学特点:
二次方:误差越大,惩罚增长得非常快。
适用场景:
回归任务的默认首选
(连续值预测:房价、温度、评分等)。
你希望模型对“大误差”反应更剧烈(因为平方会放大远离点)
缺点:
对 outlier(极端样本)特别敏感,容易被坏点拖着跑。
函数曲线
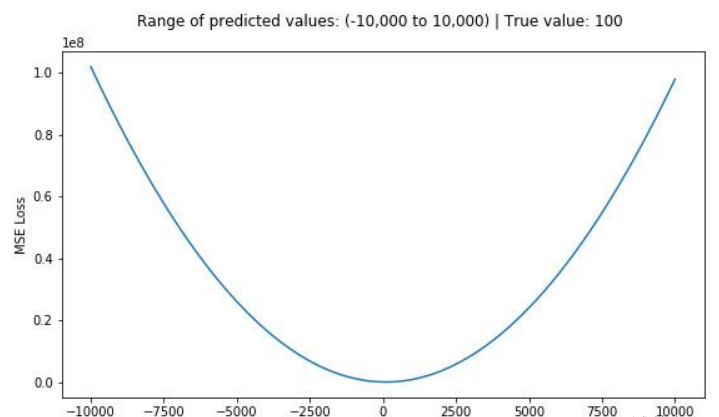
那么MAE比起MSE呢
对比 MSE:
MSE:惩罚大误差更狠,适合你希望模型尽量别出“大错”的回归;
MAE:对每个误差一视同仁,适合你想稳一点,不想被极端点绑架, 那你可以用MAE
然后上节还讲了熵
香浓信息熵:
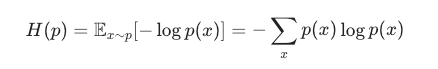
直白讲:
随机变量 X 服从分布 p
它的熵H(p) = 用分布p自己的概率,去算“平均每次观察一个样本,带来的信息量”。
再看不懂就拆开讲
设有一个随机事件x,它发生的概率是p(x)。
定义一个量:
I(x)=−logp(x)
你现在只要记两点直觉:
如果p(x)很大(比如 0.99),那−logp(x)很小
这个结果一点不意外,“信息量”小。
如果p(x)很小(比如 0.001),那−logp(x)很大
这个结果很罕见,“信息量”大。
所以:
−logp(x)被叫做“这个具体结果的惊喜度 / 信息量”。
你可以先当成定义:事件越罕见,看到它时获得的信息越多,用
−logp(x)度量。
接下来我们要讲一个概念:熵 = “信息量的平均值”
现在不只是一个结果,而是一个随机变量X:
它可能取很多种值:x1,x2,…
每个值出现的概率是p(x)
那么:
每次我们看到一个具体结果x,它的信息量是−logp(x)
但每次看到的结果不一样,信息量也会不一样。
熵H(p)做的事情就是:
用分布 p自己的概率,去算:
“平均每看到一次结果,带来的信息量是多少?”
数学上就是把“信息量”−logp(x)按概率p(x)求加权平均(期望)
这个式子就是这么来的
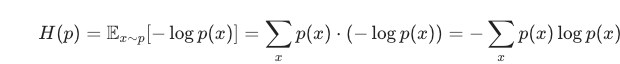
讲完了信息熵的定义了
我们为什么要讲它,不是在讲损失函数吗?
对喽,讲完了MSE,MAE回归任务经常用的损失函数,就该讲分类常用的损失函数交叉熵了,也就是cross-entropy
你看它也有entropy可见叫XX熵也算实至名归,那为什么要冠以cross呢?
我们去熵公司的前面部分,就是带期望那个
熵:
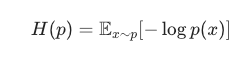
交叉熵:
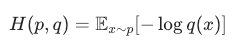
区别只在一件事:
熵:真分布p既负责说“样本出现的频率”(期望),又负责“我们认为它的概率”(log 里);
交叉熵:
所以交叉熵是个假的啊(肯定假啊,毕竟你预测的不是真值,然后去收敛模型么,对吧)
交叉熵 =“真实世界按 p出现样本,但我们用 q来编码这些样本时,平均每个样本需要多少信息量(多少 bit)”。
如果模型q跟真实p很接近,交叉熵就接近熵本身(能接近理论最优的编码长度)。
如果q很烂,把高概率事件当低概率给,交叉熵就会大很多。
分类/语言模型训练时,我们的情况刚好就是:
真实标签分布 =p(one‑hot 或经验频率,可以当“真分布”),比如LLM其实就是one-hot,不是在embedding的时候而是在词表V推理(sotamax概率)的时候其实就是一个one-hot,几万十几万的词表,只有那个词被推理出来,它是1,别人是0
模型输出的概率分布 =qθ(softmax、sigmoid 的输出)。
用的损失函数就是:
![]()
还是用llm来解释,这个时候x就是你的context,y就是你要推出来的next-token,这就好理解了吧
优化目标也是让qθ 逼近p:
![]()
哎!这就把KL散度也给引入了

,然后,下次再讲吧
讲熵,交叉熵,KL散度的关系
写在最后:我为啥又把这些东西翻出来了,是因为我发现RL的东西对大多数人太抽象了(好多读者都希望我更新,但是属实有很多人留言看不懂,其实没很多人,因为纯讲算法的,几乎没什么人读

)但是抽象的核心原因,好像并不是RL本身,反而是这些最普通的基础概念,所以我决定先给读者补补基础,否则后面ppo为什么要用grpo取代
grpo的为什么有的论文把KL散度直接删了,不弄清楚这些底层概念,读者是看不懂的,不过这个东西长一长也许能长成一本深度学习数学红宝书也不一定






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








