计算机的运算方法
基础知识
- 一个负数加上 “模(mod)” 即得该负数的补数
- 一个正数和一个负数互为补数时,它们绝对值之和即为模数
- 当真值为负时,补码可用原码除符号位外每位取反,末位加1求得
- 当真值为负时,原码可用补码除符号位外每位取反,末位加1求得
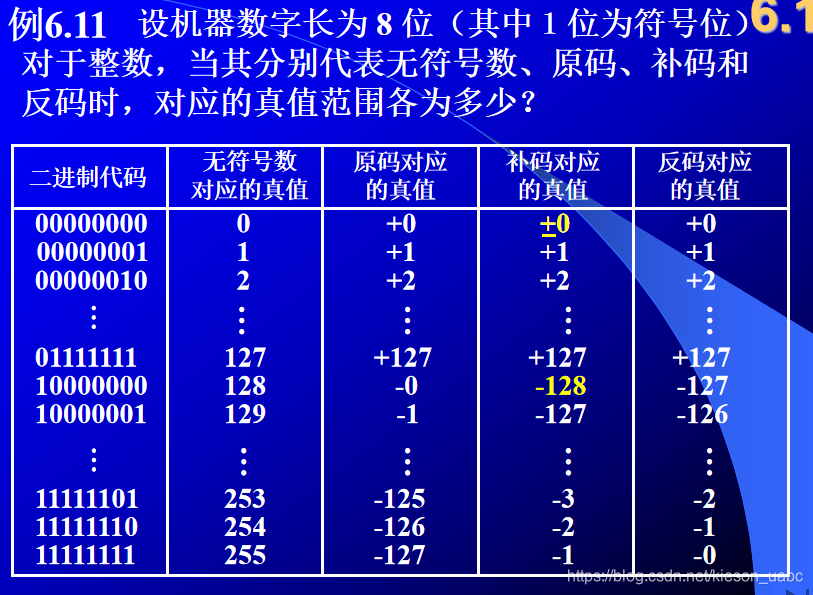
- 结论:由于0在补码中只有一种表示形式,故补码比反码和原码可以多表示一个负数
- 由y补求-y补

- 补码与移码只差一个符号位
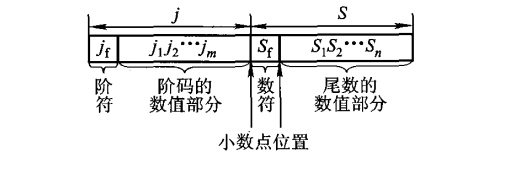
- 规格化数
- 将尾数的最高位为1的浮点数称为规格化数
- 计算机中规定浮点数的尾数用纯小数表示,即0.
- 尾数决定正负,阶码决定大小
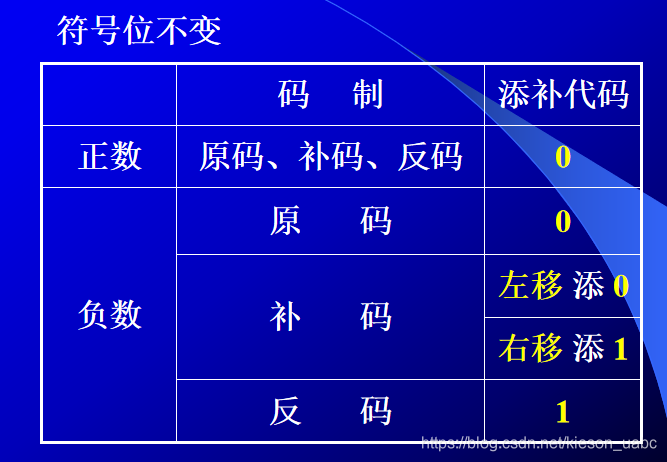
- 算数移位规则
- 整数和小数补码的公式求法
- 1.整数

- n为整数表示成二进制以后的位数(除符号位以外)
- n=1时,整数的补码叫做变形补码
- 2.小数

- 1.整数
- -1.0000的补码和原码
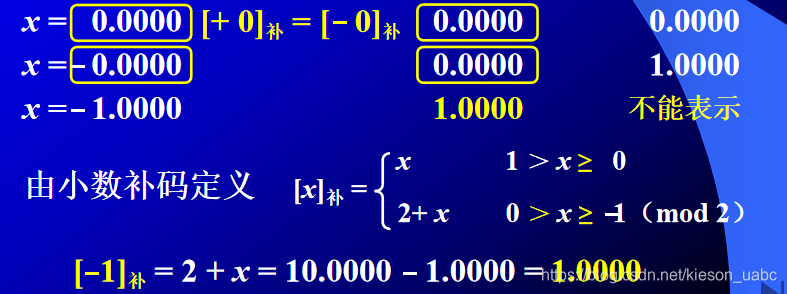
- 算术移位和逻辑移位的区别
- 算术移位:有符号数的移位
- 逻辑移位:无符号数的移位
- 逻辑左移 :低位添 0,高位移丢
- 逻辑右移 :高位添 0,低位移丢
加减法运算
- 补码加减法
- [A+B]补=[A]补+[B]补;[A-B]补=[A]补+[-B]补
- 注意事项:连同符号位一起相加,符号位产生的进位自然丢掉
- 溢出判断
- 一位符号位判溢出
- 最高有效位的进位 异或 符号位的进位 = 1,则溢出
- 两位符号判溢出

- 结果的双符号位 不同,则溢出
- 注意:最高符号位 代表其 真正的符号
- 一位符号位判溢出
乘法运算
- 笔算乘法
- 原码的运算
- 逻辑移位
- 为什么2的-1次是逻辑移位(逻辑右移)?
- 因为符号位单独处理,剩下的就是无符号数

- 原码乘法—> 符号位 和 数值位部分 分开运算
- 原码一位乘
- 乘积的符号位单独处理:异或
- 数值部分为绝对值相乘
- 每次用乘数的末位判断加被乘数还是加0
- 过程与笔算乘法完全相同
- 右移采用逻辑右移
- 原码两位乘
- 乘积的符号位单独处理:异或
- 数值部分为绝对值相乘
- 每次用乘数的2位判断原部分积是否加和如何加被乘数
-
- 计算机只能判断2的幂次,加3倍的被乘数如何处理?1+2呢?还是4-1呢?
- 答案是4-1,先减1倍的被乘数,再加4倍
- 利用标志位,标志位为0,加4倍等价于现在的标志位为1,加1倍
- 答案是4-1,先减1倍的被乘数,再加4倍
- 计算机只能判断2的幂次,加3倍的被乘数如何处理?1+2呢?还是4-1呢?
- 右移采用补码右移
- 原码一位乘
- 补码乘法
- 补码一位乘(连同符号位一起右移)
-
- 被乘数任意,乘数为正
- 被乘数任意,乘数为负
- 被乘数任意,乘数任意(booth算法)
Booth算法



- 补码一位乘(连同符号位一起右移)
除法运算
- 原码除法
-
恢复余数法
- 运算规则
- 余数 Ri>0 上商 “1”, 2Ri – y*
- 余数 Ri<0 上商 “0”, Ri + y* 恢复余数
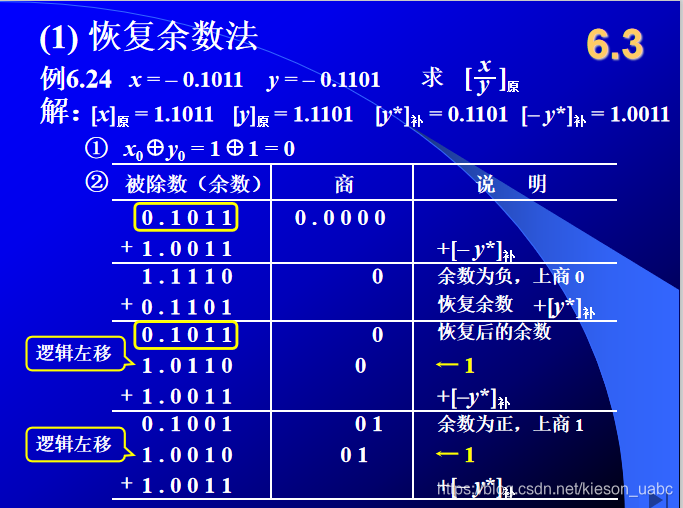
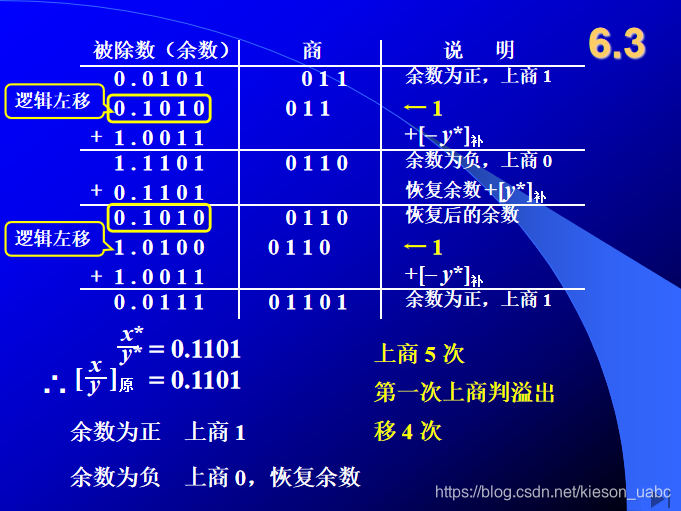
- 运算规则
-
不恢复余数法(加减交替法)
- 运算规则
- 上商“1” 2Ri – y*
- 上商“0” 2Ri + y*

- 运算规则
-
- 补码除法(加减交替法)
-
上商规则
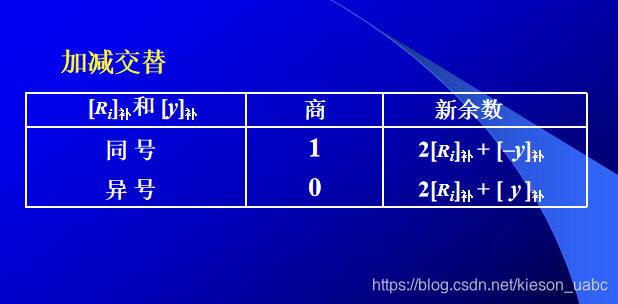

-
案例
-
浮点四则运算
浮点加减法
- 对阶原则:小阶向大阶看齐
- 规格化原则
- 原码:不论正数,负数,第一数位为1
- 补码:符号位和第一数位不同

- 左规和右规
- 左规:尾数左移 阶码减
- 右规:尾数右移 阶码加
- 当尾数溢出时,即尾数出现01. ×××或 10. ×××时,右规
- 例题
浮点乘除法
- 阶码采用补码定点加减法
- 尾数乘除同定点运算
- 规格化





 本文深入解析了计算机内部的运算方法,包括补码、反码、原码的概念及其转换,算术移位与逻辑移位的区别,加减乘除法的实现原理,以及浮点数的运算规则。通过详细讲解,帮助读者理解计算机如何处理各种数学运算。
本文深入解析了计算机内部的运算方法,包括补码、反码、原码的概念及其转换,算术移位与逻辑移位的区别,加减乘除法的实现原理,以及浮点数的运算规则。通过详细讲解,帮助读者理解计算机如何处理各种数学运算。



















 1543
1543

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










