代码随想录_数组_代码随想录区间和的复杂度-优快云博客

代码随想录01

数组

69.x的平方根

69. x 的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

思路:

思路一: 牛顿迭代法
- 时间复杂度：O(log_x_)，此方法是二次收敛的，相较于二分查找更快。
- 空间复杂度：O(1)。
思路二: 二分法
- 时间复杂度：O(log_x_)，即为二分查找需要的次数。
- 空间复杂度：O(1)。

代码:

思路一

class Solution {
    public int mySqrt(int x) {
        if(x == 0 || x == 1) {
            return x;
        }
        double x0 = x,x1 = -1;// x0: 上一次估算值 x1: 此次估算值
        while(true) {
            x1 = (x0 + x/x0) / 2.0;// 公式
            if(Math.abs(x1 - x0) < 1e-7) {
                break;
            }
            x0 = x1;// 更新x0
        }
        return (int)x0;// 返回整数部分
    }
}

思路二

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid; // 要设置ans,将<=x合并,x的算术平方根相乘一定不会大于x,要在<=中找最接近的
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

367.有效的完全平方数

367. 有效的完全平方数

给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。

不能使用任何内置的库函数，如 sqrt 。

思路:

思路一: 数学法
- 时间复杂度：O(√n)
- 空间复杂度：O(1)
- 1 + 3 + 5 + … + (2n - 1) = n^2
- 所有的完全平方数都可以表示为几个连续奇数相加, 可以将一个数连续减去连续的奇数, 看看最后的结果是否为0
思路二: 二分法
- 时间复杂度：O(log_x_)，即为二分查找需要的次数。
- 空间复杂度：O(1)。
- 若 $ xx < num $ 那么x一定在$ √num $ 的左侧, 若 $ xx > num $ 那么x一定在$ √num $ 的右侧, 否则x即为 $ √x $

代码:

法一:

class Solution {
    public boolean isPerfectSquare(int num) {
        int n = 1;
        while(num > 0) {
            num -= n;
            n += 2;
        }
        return num == 0;
    }
}

法二:

class Solution {
    public boolean isPerfectSquare(int num) {
        long l = 0,r = num;
        while(l <= r) {
            long m = l + ((r - l) >> 1);
            if(m * m < num) {
                l = m + 1;
            }else if(m * m > num){
                r = m - 1;
            }else{
                return true;// 结果一定是一个整数, 可以不合并
            }
        }
        return false;
    }
}

27.移除元素

https://leetcode.cn/problems/remove-element/description/

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。

思路:

快慢指针, 快指针负责挑选符合要求的数字, 慢指针负责设置新数组
注意: 当跳出for时, s指在下一个要放的位置, 即s的值就为新数组的有效长度

代码:

时间复杂度O(n) 空间复杂度O(1)

class Solution {
    public int removeElement(int[] nums, int val) {
        int s = 0;
        for(int f = 0;f < nums.length;f++) {
            if(nums[f] != val) {
                nums[s++] = nums[f];
            }
        }
        return s;
    }
}

26.删除有序数组中的重复项

26. 删除有序数组中的重复项

给你一个 非严格递增排列 的数组 nums ，请你** 原地** 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。

思路:

快慢指针, 慢指针指向新数组中下一个元素要放置的位置, 快指针在前面筛选, 由于相同元素相邻, 因此只需要判断相邻元素是否相同, 若
- 若当前元素和前一个元素相同, 不加入新数组中, 否则, 加入新数组中

代码:

时间复杂度O(n) 空间复杂度O(1)

class Solution {
    public int removeDuplicates(int[] nums) {
        int s = 1;
        for(int f = 1;f < nums.length;f++) {
            if(nums[f] != nums[f - 1]) {
                nums[s++] = nums[f];
            }
        }
        return s;
    }
}

283.移动零

283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

思路:

快慢指针，快指针依次遍历整个数组，若当前元素不为零，则放置在慢指针的位置，慢指针后移一位，否则不做操作，最终所有非零元素会在相对次序不变的情况下保存在数组前面，0均位于末尾。

代码:

时间复杂度：O(n)
空间复杂度：O(1)

class Solution {
    public void moveZeroes(int[] nums) {
        if(nums == null) return;

        int f = 0,s = 0;
        for(f = 0;f < nums.length;f++) {
            if(nums[f] != 0) { // 不等于0, 换到前面
                int t = nums[f];
                nums[f] = nums[s];
                nums[s++] = t;
            }
        }
    }
}

844.比较含退格的字符串

844. 比较含退格的字符串

给定 s 和 t 两个字符串，当它们分别被输入到空白的文本编辑器后，如果两者相等，返回 true 。# 代表退格字符。

**注意：**如果对空文本输入退格字符，文本继续为空。

思路:

将每个字符串转为字符数组，从后往前遍历，使用变量n来记录尚未消耗的 ‘#’
若当前字符是 ‘#’ ，n++
若当前字符的 n == 0 ，说明此时没有需要消耗的 ‘#’
否则，当前字符有对应需要消耗的 ‘#’ ，n–，通过当前的字符，继续循环

代码:

时间复杂度 O(M + N) , 遍历两个字符串的时间
空间复杂度 O(1)

class Solution {
    public boolean backspaceCompare(String s, String t) {
        return convert(s).equals(convert(t));
    }

    public String convert(String s) { // 转换出使用'#'退格后的字符串
        StringBuilder builder = new StringBuilder();// 用于保存转换后的字符串
        char[] cs = s.toCharArray();// 原来的字符串转换出的数组
        int n = 0;// 尚未消耗的'#'的数量

        for(int i = cs.length - 1;i >= 0;i--) {
            if(cs[i] == '#') { // 若当前字符为'#', 尚未消耗的'#'数加一
                n++;
            }else if (n == 0) { // 若当前没有尚未消耗的'#', 将当前的字符追加入答案
                builder.append(cs[i]);
            }else { // 消耗'#'
                n--;
            }
        }

        return builder.toString(); // 返回
    }
}

977.有序数组的平方

977. 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序

进阶：

请你设计时间复杂度为 O(n) 的算法解决本问题

思路

绝对值相对大的一定在两边，从两边开始往中间走，取出两者中较大的那一个放入收集数组中，同时数组的指针前移

代码

class Solution {
    public int[] sortedSquares(int[] nums) {
        int n = nums.length;
        int[] ans = new int[n]; // 返回值
        int i = 0;// 从前往后
        int j = n - 1;// 从后往前

        for(int p = n - 1;p >= 0;p--) { // 从后往前填充答案数组
            int x = nums[i] * nums[i]; // 前面值的平方
            int y = nums[j] * nums[j]; // 后面值的平方
            if(x > y) { // 前面值的平方大
                ans[p] = x; // 将大的填充在p位值
                i++; // 前指针后移
            }else{ // 后面值的平方大于等于前面值的平方
                ans[p] = y; // 将大的填充在p位值
                j--; // 后指针前移
            }
        }

        return ans; // 返回答案
    }
}

209.长度最小的子数组

209. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

提示：

1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5

思路

暴力解法:

这道题目暴力解法当然是两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2)

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; // 最终的结果
        int sum = 0; // 子序列的数值之和
        int subLength = 0; // 子序列的长度
        for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
            sum = 0;
            for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
                sum += nums[j];
                if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                    subLength = j - i + 1; // 取子序列的长度
                    result = result < subLength ? result : subLength;
                    break; // 因为我们是找符合条件最短的子序列，所以一旦符合条件就break
                }
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

时间复杂度：O(n^2)
空间复杂度：O(1)

后面力扣更新了数据，暴力解法已经超时了。

滑动窗口:

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

窗口就是满足其和 ≥ s 的长度最小的连续子数组。
窗口的起始位置如何移动：如果当前窗口的值大于等于s了，窗口就要向前移动了（也就是该缩小了）。
窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

为什么时间复杂度是O(n) ?

每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。

解答

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        // 1. 初始化变量left, result, sum
        int left = 0;
        int result = Integer.MAX_VALUE;
        int sum = 0;
        // 2. 滑动right, 判断sum >= target
        for(int right = 0;right < nums.length;right++) {
            sum+=nums[right];
        // 2.1 sum >= left : 循环右移left, sum-nums[left]
        // 2.2 sum < left : 右移right, 扩张滑动窗口, 增大sum
            while(sum >= target) {
                result = Math.min(result,right - left + 1);
                sum-=nums[left++];
            }
        }

        // 3. 判断res是否为最大值, 不是返回res, 否则返回0
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

904.水果成篮

904. 水果成篮

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果种类。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

你只有两个篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘，你必须从每棵树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的最大数目。

提示：

1 <= fruits.length <= 105
0 <= fruits[i] < fruits.length

思路:

滑动窗口

代码:

class Solution {
    public int totalFruit(int[] fruits) {
        // 1. 初始化变量
        int n = fruits.length;
        int[] hash = new int[n];// 模拟hash表, 作为篮子, 数组下标就是水果的种类, 数组的值就是该类水果的个数
        int left = 0;// 左指针
        int res = 0;// 返回值
        int kind = 0;// 种类数

        // 2. 开始滑动, 向篮子中放入水果, 判断放入后kind是否>2
        for(int right = 0;right < n;right++) {
            int in = fruits[right];
            if(hash[in] == 0) kind++;// 如果是第一次放入该类水果, 类型+1
            hash[in]++;// 该类水果的个数+1

            // 2.1 >2, 开始从left位置拿出水果
            while(kind > 2) {
                int out = fruits[left];
                hash[out]--;// 开始拿出该类水果
                if(hash[out] == 0) kind--;// 如果该种水果拿完, 类型-1
                left++;// 更新左指针的位置
            }

            // 3. 更新res
            res = Math.max(res,right - left + 1);
        }
        
        // 4. 返回
        return res;
    }
}

76.最小覆盖子串

76. 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

示例 2：

输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。

示例 3:

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

m == s.length
n == t.length
1 <= m, n <= 105
s 和 t 由英文字母组成

思路: 滑动窗口

代码:

    public static String minWindow(String str, String tar) {
        // 1. 判断s是否足够比较
        if (str.length() < tar.length()) {
            return "";
        }
        
        // 2. 初始化变量, 建表
        char[] s = str.toCharArray();
        char[] t = tar.toCharArray();
        int[] cnts = new int[123];// 欠债表:下标表示该下标对应的字母位置,值为该字母欠债情况
        // 根据tar初始化欠债表
        for (char cha : t) {
            cnts[cha]--; // --表示欠债需还
        }
        // 最小覆盖子串的长度
        int len = Integer.MAX_VALUE;
        // 从哪个位置开头，发现的这个最小覆盖子串
        int start = 0;
        
        // 3. 开始滑窗
        for (int l = 0, r = 0, debt = t.length; r < s.length; r++) {
            // 3.1 更新欠债表
            // s[r] 当前字符 -> int
            // cnts[s[r]] : 当前字符欠债情况，负数就是欠债，正数就是多给的
            if (cnts[s[r]]++ < 0) { // <0: 加完后<0就要还款,如果是=0,只能在还完的时候计数
                debt--;
            }
            
            // 3.2 判断是否依旧欠债
            // 3.2.1 不欠债
            if (debt == 0) {
                // r位置结尾，真的有覆盖子串！
                // 3.2.1.1 看看这个覆盖子串能不能尽量短
                while (cnts[s[l]] > 0) {
                    // l位置的字符能拿回
                    cnts[s[l++]]--;
                }
                // 从while里面出来，
                // l....r就是r位置结尾的最小覆盖子串
                
                // 3.2.1.2 更新改变窗口后len的大小(要放在if里面,否则len将不正确)
                if (r - l + 1 < len) {
                    len = r - l + 1;
                    start = l;
                }
            }
        }
        
        // 4. 返回
        return len == Integer.MAX_VALUE ? "" : str.substring(start, start + len);
    }

59.螺旋矩阵

59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例：

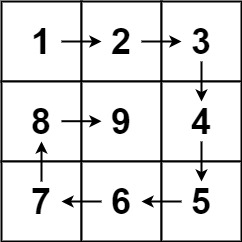
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

提示：

1 <= n <= 20

思路:

按照上右下左的顺序进行填充, 每次要坚持循环不变量原则, 每一行/列遍历时都从第一个开始填充, 不填充最后一个.

代码:

class Solution {
    public int[][] generateMatrix(int n) {
        // 1. 初始化
        int startX = 0,startY = 0,loop = 1,count = 1,offset = 1;
        // startX startY控制左上边界; n - offset控制右下边界
        int i,j;
        int[][] nums = new int[n][n];
        // 2. 循环
        while(loop <= n / 2) {
            // 上
            for(j = startY;j < n - offset;j++) {
                nums[startX][j] = count++;
            }
            // 右
            for(i = startX;i < n - offset;i++) {
                nums[i][j] = count++;
            }
            // 下
            for(;j > startY;j--) {
                nums[i][j] = count++;
            }
            // 左
            for(;i > startX;i--) {
                nums[i][j] = count++;
            }
            
            // 更新变量
            startX++;
            startY++;
            loop++;
            offset++;
        }

        // 3. 根据n是否为奇数填充剩下的位置
        if(n % 2 == 1) {
            nums[startX][startY] = count;
        }

        // 4. 返回
        return nums;
    }
}

54.螺旋矩阵

54. 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

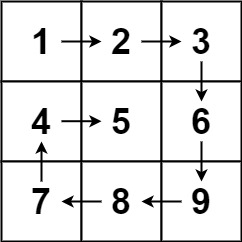
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

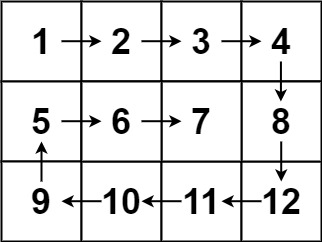
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

思路:

每一次遍历一整行/列, 通过控制u ,d ,l ,r 四个变量来控制需要进行遍历的边界

代码:

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ans = new ArrayList<>();
        // 0. 特殊判断
        if(matrix.length == 0) return ans;
        // 1. 初始化
        int u = 0,d = matrix.length - 1,l = 0,r = matrix[0].length - 1;

        // 2. 循环
        while(true) {
            // 上
            for(int i = l;i <= r;i++) ans.add(matrix[u][i]);
            if(++u > d) break;
            // 右
            for(int i = u;i <= d;i++) ans.add(matrix[i][r]);
            if(--r < l) break;
            // 下
            for(int i = r;i >= l;i--) ans.add(matrix[d][i]);
            if(--d < u) break;
            // 左
            for(int i = d;i >= u;i--) ans.add(matrix[i][l]);
            if(++l > r) break;
        }

        // 3. 返回
        return ans;
    }
}

58. 区间和

题目链接

题目描述

给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。

输入描述

第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间，直至文件结束。

输出描述

输出每个指定区间内元素的总和。

输入示例

输出示例

3
9

数据范围：

0 < n <= 100000

思路:

前缀和

代码:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(System.out);

        // 1. 读取数组长度 n
        in.nextToken();
        int n = (int) in.nval;

        // 2. 初始化数组和前缀和数组
        int[] arr = new int[n];
        int[] prefixSum = new int[n];
        int sum = 0;

        // 3. 读取数组并计算前缀和
        for (int i = 0; i < n; i++) {
            in.nextToken();
            arr[i] = (int) in.nval;
            sum += arr[i];
            prefixSum[i] = sum;
        }

        // 4. 处理查询
        while (in.nextToken() != StreamTokenizer.TT_EOF) {
            int a = (int) in.nval; // 起始索引 a
            in.nextToken();
            int b = (int) in.nval; // 结束索引 b

            // 5. 计算区间和并输出
            int result = (a == 0) ? prefixSum[b] : prefixSum[b] - prefixSum[a - 1];
            out.println(result);
        }

        // 6. 关闭输出流
        br.close();
        out.flush();
        out.close();
    }
}

44.开发商购买土地

题目链接

题目描述

在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。

现在，需要将这个城市区域的所有区块分配给 A 公司和 B 公司。

然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。为了确保公平竞争，你需要找到一种分配方式，使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。

注意：区块不可再分。

输入描述

第一行输入两个正整数，代表 n 和 m。

接下来的 n 行，每行输出 m 个正整数。

输出描述

请输出一个整数，代表两个子区域内土地总价值之间的最小差距。

输入示例

输出示例

思路:

$ O(n^2) $

(1) 前缀和: 计算每行每列的前缀和

(2) 暴力法: 每一次遍历的行/列尾时更新result

代码:

(1) 前缀和

import java.io.BufferedReader;
import java.io.StreamTokenizer;
import java.io.PrintWriter;
import java.io.InputStreamReader;
import java.lang.Math;

public class Main {
    public static void main(String[] args) throws Exception{
        
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(System.out);
    // 1. 统计总和
        // 1.1 输入n, m, arr
        in.nextToken();
        int n = (int)in.nval;
        in.nextToken();
        int m = (int)in.nval;
        int sum = 0;
        
        int[][] nums = new int[n][m];
        for(int i = 0;i < n;i++) {
            for(int j = 0;j < m;j++) {
                in.nextToken();
                nums[i][j] = (int)in.nval;
                sum += nums[i][j];
            }
        }
        
    
    // 2. 统计行和
        int[] horizontal = new int[n];
        for(int i = 0;i < n;i++) {
            for(int j = 0;j < m;j++) {
                horizontal[i] += nums[i][j];
            } 
        }
    
    // 3. 统计列和
        int[] vertical = new int[m];
        for(int j = 0;j < m;j++) {
            for(int i = 0;i < n;i++) {
                vertical[j] += nums[i][j];
            }
        }
    
    // 4. 遍历前缀和, 计算最小值   
        int result = Integer.MAX_VALUE;
        // 4.1 行
        int horizontalCut = 0;
        for(int i = 0;i < n;i++) {
            horizontalCut += horizontal[i];
            result = Math.min(result,Math.abs(sum - 2 * horizontalCut));
        }
    
        // 4.2 列    
        int verticalCut = 0;
         for(int j = 0;j < m;j++) {
            verticalCut += vertical[j];
            result = Math.min(result,Math.abs(sum - 2 * verticalCut));
        }   
        
        out.println(result);
        out.flush();
        br.close();
        out.close();
    
    }
    
}

(2) 暴力破解

import java.io.BufferedReader;
import java.io.StreamTokenizer;
import java.io.PrintWriter;
import java.io.InputStreamReader;
import java.lang.Math;

public class Main {
    public static void main(String[] args) throws Exception{
        
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(System.out);
    // 1. 统计总和
        // 1.1 输入n, m, arr
        in.nextToken();
        int n = (int)in.nval;
        in.nextToken();
        int m = (int)in.nval;
        int sum = 0;
        
        int[][] nums = new int[n][m];
        for(int i = 0;i < n;i++) {
            for(int j = 0;j < m;j++) {
                in.nextToken();
                nums[i][j] = (int)in.nval;
                sum += nums[i][j];
            }
        }
        
    
    // 2. 遍历每行/列, 计算最小值   
        int count = 0, result = Integer.MAX_VALUE;
        // 2.1 行
        for(int i = 0;i < n;i++) {
            for(int j = 0;j < m;j++) {
                count += nums[i][j];
                if(j == m - 1) result = Math.min(result,Math.abs(sum - 2 * count));
            }
        }
    
        // 2.2 列    
        count = 0;
        for(int j = 0;j < m;j++) {
            for(int i = 0;i < n;i++) {
                count += nums[i][j];
                if(i == n - 1) result = Math.min(result,Math.abs(sum - 2 * count));
            }
        }  
        
        out.println(result);
        out.flush();
        br.close();
        out.close();
    
    }
    

}