二分图最小点覆盖小结

最小点覆盖：

我的总结:最小点覆盖：找出一个最小点集使得这个图的的每条边至少和这个点集的一个顶点连接

形象上描述：即找出最少的红点使得每条边至少连接一个红色顶点(每条边最多连接两个红点)

下图来自别人的博客

下面给出顶点覆盖问题的描述： 

给定一个无向图：G=(V, E)和一个正整数k，判定是否存在一个顶点子集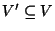，其中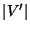=k，使得对于任意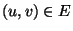有u∈V'或 v ∈V' 。如果存在这样的V'，就称顶点子集V'为图G的一个大小为k的顶点覆盖。如下图所示，红色圆圈表示其所在无向图的一个顶点覆盖。

 

 

第一个图：k=3  第二个图：k=4

 

最小顶点覆盖问题实质上就是求最小k（用k'表示最小k值）的问题，用一句话来概括最小顶点覆盖问题就是：找出给定图G中覆盖每条边的最小顶点子集。如下图所示，红色圆圈表示其所在图的一个最小顶点覆盖。

 

 

第一个图：k'=2  第二个图：k'=3

 

DAG图的最小路径覆盖：