LeetCode 334. Increasing Triplet Subsequence-优快云博客

本文探讨了在数组中寻找递增三元组的问题，首先尝试了使用动态规划的方法，但时间复杂度过高。随后提出了一种线性时间和常数空间的解决方案，通过维护两个变量s和m来记录序列中的最小和次小元素，从而简化了问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

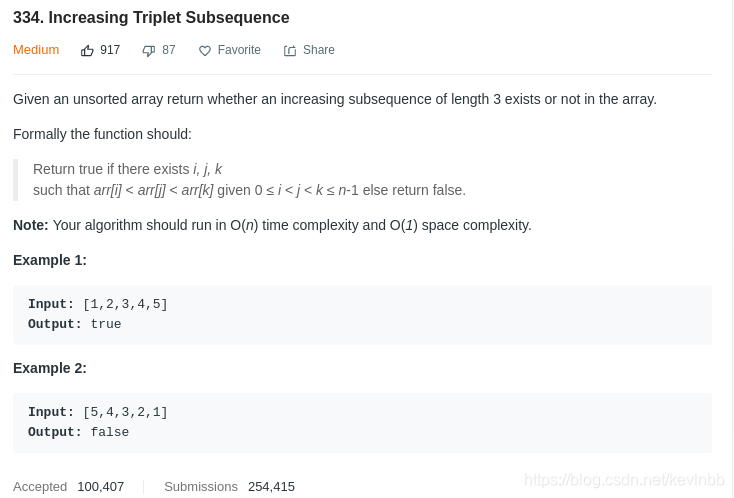
题目

在这里插入图片描述

分析

看到题目的第一想法就是用dp来优化时间，dp[i]表示i号下标元素之前比该元素小的元素数量，初始化全为0，当dp[i]等于2的时候，就意味存在这样的三元组，返回true

代码如下：

class Solution {
public:
    bool increasingTriplet(vector<int>& nums) {
        if (nums.size() <= 2) return false;
        vector<int>dp (nums.size(), 0);
        for (int i = 1; i < nums.size(); ++i) {
            for (int j = 0; j < i; ++j) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
                if (dp[i] == 2) return true;
            }
        }
        return false;
    }
};

然而平方级别的时间性能和线性的空间性能都不满足题目要求，虽然能过oj，但是评分很差。
题目要求使用线性的时间性能和置地空间的算法。由于题目只需要找出三个递增的序列，我的想法就是利用三个指针或者三个变量s，m，l来记录当前记录到的大中小三个元素，那问题的关键就是如何来更新这三个元素的值，因为要保证是按前后顺序出现的序列，控制三个变量的变化很复杂，所以换了一种思路。
其实只需要维护两个量，就是三元组中第三大的变量s和第二大的变量m即可，当遇到比s小的，就更新s为更小的值，这样才可能在后面得三元组，当遇到比s大比m小的，就更新m为这个值，道理是一样的，这样当出现了比m还大的元素就意味存在这样的三元组。
那如何设置这三个数的初值呢？有个好的技巧是把s和m都设成int最大值，而且按照s先更新的顺序来处理，这样就能保证s和m的序列顺序，代码如下：

class Solution {
public:
    bool increasingTriplet(vector<int>& nums) {
        int s = INT_MAX, m = INT_MAX;
        
        for (int i = 0; i < nums.size(); ++i) {
            if (s >= nums[i]) {
                s = nums[i];
            }
            else if (m >= nums[i]) m = nums[i];
            else return true;
        }
        return false;
    }
};